Регулярные графы

Одним из методов построения топологических структур сетей с заданными свойствами является синтез графов с помощью известных математических операций. На рис. 8 приведен граф, построенный таким путем. Обычно такие графы обладают некоторой регулярностью, т.е. все их узлы равноправны в смысле топологии сети.

Граф Петерсона, изображенный на рис. 2.1, состоит из 10 узлов и 15 линий со связностью 3. Степень каждого узла также равна трем, и, следовательно, связность этого графа максимальна. Говорят, что такой граф имеет максимальную связность. Другое свойство оптимальности графа Петерсона связано с диаметром графа, т.е. максимальным расстоянием между парами узлов сети, измеряемым числом "шагов" от узла к узлу. На втором уровне будет три узла, так как степень исходного узла была равна трем. По той же причине каждый из трех узлов второго уровня будет соединен не более чем с двумя узлами третьего уровня. На расстоянии двух шагов от исходного будет не более 10 узлов, включая и его самого. Таким образом, граф степени 3 и диаметра 2 не может содержать более десяти узлов. Этот максимум достигается на графе Петерсона.

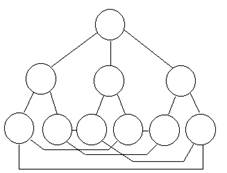
Рис. 2.1. Граф Петерсона

Регулярные графы такого типа представляют большой теоретический интерес и могут оказаться полезными на практике при конструировании коммутаторов из одинаковых компонентов. В коммутации каналов уже сейчас используются регулярные соединения компонент, и, если экономика производства будет и дальше развиваться в том же направлении, это может стать характерной чертой коммутации вообще. При построении крупномасштабных сетей связи с географически далеко отстоящими друг от друга узлами регулярные синтезированные графы едва ли найдут применение, поскольку стоимость линий связи, являющихся важными параметрами оптимизации, сильно меняется в зависимости от географических факторов.

Важным элементом является определение связности и реберной связности графа. В связности небольшой сети можно легко убедиться простой проверкой. Для больших сетей проверка связности представляет весьма сложную задачу, которая тем не менее весьма часто встречается на практике.