Лоренц шарттары. Потенциалдарға арналған теңдеулер

Қозғалыстағы зарядталған бөлшектерге магнит өрісі тарапынан әсер ететін күш Лоренц күші деп аталады.

F_Л =qυBsin α.

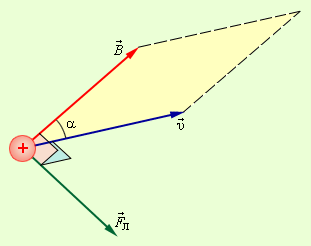
Мұндағы a - В және u векторлары арасындағы бұрыш. Ампер күшінің бағыты секілді, Лоренц күшінің бағыты сол қол ережесімен анықталады.

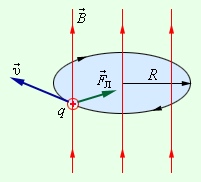Біртекті магнит өрісінде оның индукциясына перпендикуляр u жылдамдықпен қозғалған зарядты бөлшекке модулі жағынан тұрақты, жылдамдыққа перпендикуляр бағытталған Лоренц күші әсер етеді. Лоренц күшінің әсерімен бөлшек центрге тартқыш үдеу алады және шеңбер бойымен қозғалады, мұнда Лоренң күші жұмыс істемейді. Шеңбердің радиусы: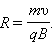

Электр тогы-зарядалған бөлшектердің реттелген бағытталған қозғалысы.Токтың бағытына оң зарядталған бөлшектердің қозғалыс бағыты алынады.Токтың әсері: 1)боймен ток жүрген өткізгіш қызады.2)химиялық әсері байқалады.3)Магниттік әсері байқалады.Электр тогы болу үшін мына шарттар орындалу қажет:1)Зарядталған бөлшектер q.2)Өріс тарапынан әсер ететін күш болу керек(F=qE).3)Электр өрісі Е.4)Потенциял айырмасы U болу керек.

Сыртқы магнит өрісі 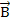-де орналасқан ток элементі Idl -ді қарастырайық.Бұл векторлардың арасындағы бұрышыт 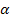болсын.Ампер күшіне сәйкес Idl элементіне мынадай күш әсер етеді

dF=BIdl

мұндағы ток күші

I= 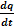q=lN

Осы бірінші өрнекті екіншісіне қою нәтижесінде мынаны шығарып аламыз:dF=BdlN 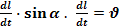зарядтың қозғалыс жылдамдығы болатындықтан жоғарыдағы өрнектен

F_n=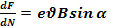

Векторлық формада өрнегі былайша жазылады,яғни

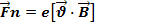
Магнит өрісінде қозғалатын зарядқа әсер ететін күш 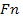-ді Лоренц анықтаған, сондықтан бұл Лоренц күші деп аталған.Сол қол немесе бұранда ережесі бойынша бұл күштің 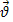және 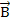векторлары жататын жазықтыққа перпендикуляр болатынын байқйамыз.Сондықтан бұль күш жылдамдықтың шамасын өзгерте алмайды,тек оның бағытын ғана өзгерте алады.Олай болса, Лоренц күші центрге тартқыш күш болып табылады:

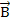=const және 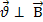болғанда

q 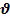B=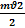

Өрнек 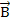өрісіндегі зарядтың қозғалыс параметрлерін табуға арналған өрнек болады

Электр өрісінің потенциалы– скалярлық шама, өрістің берілген нүктесіндегі потенциалық энергияның, сыншы зарядқа қатынасы 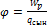. .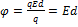Бұдан потенциал өрістің энергетикалық сипаттамасын беретін физикалық шама екенін көреміз. Өрістің күштік сипаттамасы кернеулік және оның энергетикалық сипаттамасы – потенциалдың арасында электростатикалық өрістің потенциалдығына негізделген байланыс бар. Потенциалды күш өрісінде потенциалдық энергия мен күш арасындағы байланыс мына түрде берілген 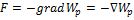.мұнд. 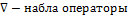, оның түрі 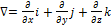, осыдан 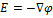. Мұндағы «минус» таңбасы Е векторының бағыты әрқашан да потенциалдың кемуіне қарай бағытталғандығын көрсетеді.

Нүктелік заряд потенциялының формуласы 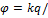Er.

Потенциялдар айырмасын өлшейтін құрал-электрометр деп аталады.Потенциал^[1] (потенциалдық функция) — физикалық күш өрістерінің кең көлемді тобын (электрлік, гравитациялық, т.б.) және физикалық шамалардың вектормен көрсетілген өрістерін (сұйықтық жылдамдығының өрісі, т.б.) сипаттайтын ұғым. Әрбір векторлық шама а өзінің потенциалының градиентіне тең: а=gradj. Мұндай жағдайда векторлық өрісті потенциалдық деп атайды. Потенциал векторлық өрісті сипаттау үшін көмекші функция ретінде енгізіледі. Термодинамикада потенциал берілген жүйе күйін сипаттаушы макропараметрлерге байланысты функция ретінде қарастырылады. Потенциал арқылы термодинам. жүйенің барлық қасиетін анықтауға болады. Физикада потенциал ұғымының басқа мағынасы да бар. Мысалы, электр өрісінде ол бірлік зарядты электр өрісінің берілген бір нүктесінен шексіздікке тасуға кеткен жұмысына тең.

Потенциал(Педагогика) - қандай да болсын міндетті шешу үшін, белгілі мақсатқа жету үшін пайдаланылуы мүмкін қайнар-көздер, мүмкіндіктер, құралдар, қорлар, белгілі бір саладағы жеке тұлғаның, қоғамның, мемлекеттің мүмкіндіктері.^[2]

Векторлық потенциал - құйынды векторлық өрісті сипаттауға арналып қолданылатын векторлық функция.^[1]

векторный потенциал — это векторное поле, ротор которого равен заданному векторному полю. Он аналогичен скалярному потенциалу, который определяется как скалярное поле, градиент которого равен заданному векторному полю.

Формально, если v — векторное поле, векторным потенциалом называется векторное поле A такое, что

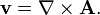
Если A является векторным потенциалом для поля v, то из тождества

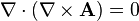
(дивергенция ротора равна нулю) следует

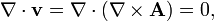
то есть v должно быть соленоидальным векторным полем.

Векторный потенциал в физике[править | править вики-текст]

Основная статья: Векторный потенциал электромагнитного поля

Уравнения Максвелла[править | править вики-текст]

Одним из способов записи уравнений Максвелла является формулировка в терминах векторного и скалярного потенциалов. Векторный потенциал 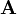вводится таким образом, что

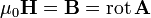(в системе СИ).

При этом уравнение 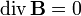удовлетворяется автоматически.

Подстановка выражения для 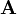в

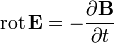
приводит к уравнению

,

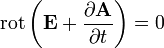согласно которому, так же как и в электростатике вводится скалярный потенциал. Однако теперь в 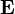вносят вклад и скалярный и векторный потенциал:

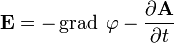
Из уравнения 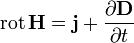следует

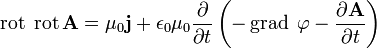
Используя равенство 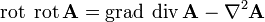, уравнения для векторного и скалярного потенциалов можно записать в виде

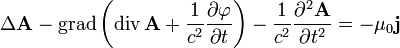
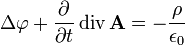
Скалярный потенциал векторного поля (чаще просто потенциал векторного поля) — это скалярная функция 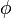такая, что во всех точках области определения поля

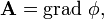
где 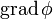обозначает градиент 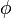. В физике обычно потенциалом называют величину, противоположную по знаку (потенциал силы, потенциал электрического поля).

25. Электрмагниттік өрістің энергия ағынының тығыздығы және энергиясының тығыздығы..

Электромагниттік толқындарды анықтау мүмкіндігі, оларды энергияны тасымалдайтынын

көрсетеді. Элмгнттк толқындар энерг.-ң w көл.-к тығ.-ғы, w(эл.) электр w(м) магниттік өрістердің көл.-к тығыздығынан қалыптасады: w = w(эл)+w(эл)= (ε0ε)E²/2 + μ0μH²/2, w(эл)=W/V=ED/2

ε0εE= μ0μH² осыны ескере отырып , уақыттың әрбір мезетіндегі эл. ж\е маг.-к өрістер энерг.-ң көлемдік тғздқнң бірдейлігін аламыз, яғни w(эл)=w(м). Сондықтан былай болады: w=2 w(эл)= ε0ε E²= .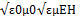

Энергияның тығыздығын ортадағы толқындардың таралу жылд.-на көбейтіп, энергия ағыны тығыздығының модулін аламыз: S=wv=EH, өйткені Е ж/e Н векторлары өзара перпенд.-р және толқындардың таралу бағытымен оң бұрандалық жүйені құрайды, сондықтан векторлар [ЕН] бағыты, энергияларды тасымалдау бағытымен сәйкес келеді, ал бұл вектордың модулі ЕН-ге тең. Элмгнттк энергия ағынының тығыздық векторы Умов-Поитинг векторы деп аталады: S=[EH]