Электрстатикалық өрістегі механикалық күштер.
Электрстатикалық өрісте сыншы Q0 зарядты шексіз аз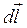 
орын ауысты-руда кулондық күштердің атқаратын элементар жұмысы:
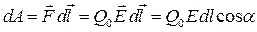. (104)
Нүктелік Q зарядтың электрстатикалық өрісінде Q0 зарядтың шексіз аз 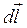орын ауыстыруында атқарылатын элементар жұмыс:
,
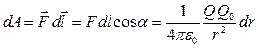ал 1 нүктеден 2 нүктеге орын ауыстыруда атқарылатын жұмыс:
.
Кез келген L тұйық контур бойында Q заряд айнала қозғалғанда:
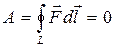. (105)
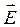векторының циркуляциясы туралы теорема: Электрстатикалық өріс кернеулігі векторының кез келген тұйық контур бойымен циркуляциясы нөлге тең болады:
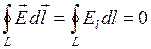. (106)
Электрстатикалық өрісқұйынсыз болғандықтан, Стокс теоремасына сәйкес, 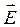кернеулігі мына шартты қанағаттандырады: 
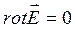. Бұл вакуумде және затта тек электрстатикалық өріс үшін ғана орындалады.
Сыншы нүктелік Q0 зарядтың нүктелік Q1, Q2 , Q3 , ..., QN зарядтар жүйесінің өрісіндегі потенциалдық энергиясыжеке зарядтарға қатысты потенциалдық энергиялардың қосындысына тең:
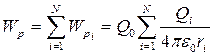. (107)
Электрстатикалық өрістің потенциалы–сан жағынанөрістің нақты нүктесінде орналасқан бірлік зарядтың потенциалдық энергиясына тең:
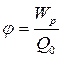. (108)
Электрстатикалық өріс күштерінің сыншы Q0 зарядты өрістің бір нүктесінен екінші нүктесіне орын ауыстыруда атқаратын жұмысыбастапқы және соңғы нүктелердің потенциалдар айырымын сыншы заряд шамасына көбейткенге тең:
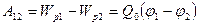(109)
15. Заттағы Максвелл теңдеулерінің формальді жүйесі, шекаралық шарттар.
Максвелл теңдеуі- классикалық электродинамиканың негізгі теңдеулері; кез келген ортадағы жэне вакуумдағы барлық электромагнит/электромагниттік кұбылыстарды толығымен сипаттайды, өріс көздерінің, электр зарядының жэнетоктардың орналасуы мен козғалысы аркылы электромагниттік өрісті сипатгайтын шамалар өзгерісін байланы- стыратын төрт тендеулер жүйесінен тұрады.Электромагниттік өріс теориясының негізін Максвелл теңдеулері деп аталатын теңдеулер жүйесі құрайды. Бұл теорияныңматематикалық аппараты күрделіболғандықтан, олтеңдеулердіқарастырмаймыз.
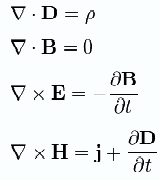
Изоторпты және дисперция жоқ ортадағы Максвелл теңдеулері:
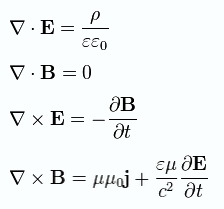
Дата добавления: 2015-01-10; просмотров: 2413;