Этапы и цели компьютерного математического моделирования

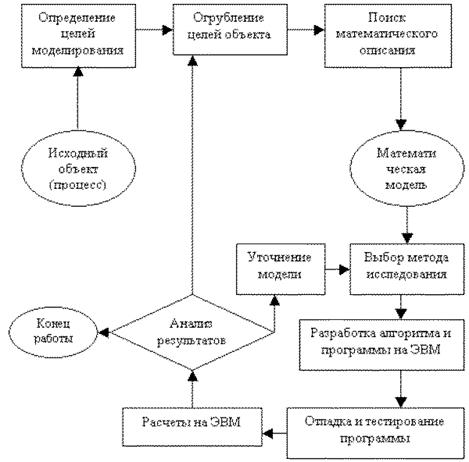
Общая схема процесса компьютерного математического моделирования

Первый этап – определение целей моделирования. Модель нужна для того, чтобы:

- понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром (понимание);

- научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);

- прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).

Второй этап – огрубление целей объекта. Определение списка величин, от которых зависит поведение объекта или ход процесса, а также тех величин, которые желательно получить в результате моделирования. Обозначим первые (входные) величины через x₁, x₂, ..., x_n вторые (выходные) через y₁, y₂, ...,y_k. Символически поведение объекта или процесса можно представить в виде:

y_j = F(x₁, x₂, ..., x_n), (j=1,2,...,k),

где F_j – те действия, которые следует произвести над входными параметрами, чтобы получить результаты. Хотя запись F(x₁, x₂, ..., x_n) напоминает о функции, здесь она используется в более широком смысле.

Входные параметры х_i, могут быть известны «точно», т.е. поддаваться (по крайней мере, в принципе) измерению однозначно и с любой степенью точности – тогда они являются детерминированными величинами. Однако, часто входные параметры известны лишь с определенной степенью вероятности, т. е. являются случайными (стохастическими). Случайный – не значит непредсказуемый; просто характер исследования меняется (он приобретают вид «С какой вероятностью...», «С каким математическим ожиданием...» и т.п.). Для стохастической модели выходные параметры могут быть как величинами вероятностными, так и однозначно определяемыми. Пример последнего: на перекрестке улиц можно ожидать зеленого сигнала светофора и полминуты, и две минуты (с разной вероятностью), но среднее время ожидания есть величина вполне определенная, и именно она может быть объектом моделирования.

Разделение входных параметров по степени важности влияния их изменений на выходные называется ранжированием (разделением по рангам). Чаще всего невозможно (да и не нужно) учитывать все факторы, которые могут повлиять на значения исследуемых величин. От того, насколько умело выделены важнейшие факторы, зависит успех моделирования, быстрота и эффективность достижения цели. Выделить более важные (или, как говорят, значимые) факторы и отсеять менее важные может лишь специалист в той предметной области, к которой относится модель. Умело ранжированная модель должна быть адекватна исходному объекту или процессу в отношении целей моделирования. Обычно определить, адекватна ли модель можно только в процессе экспериментов с ней, и анализа результатов.

Третий этап – поиск математического описания. На этом этапе необходимо перейти от абстрактной формулировки модели к формулировке, имеющей конкретное математическое наполнение. Именно на этом этапе получается математическую модель, которая предстает в виде уравнения, системы уравнений, системы неравенств, дифференциального уравнения или системы таких уравнений.

Четвертый этап – выбор метода исследования. Как правило, для решения одной и той же задачи есть несколько конкретных методов, различающихся эффективностью, устойчивостью и т.д. От верного выбора метода часто зависит успех всего процесса.

Пятый этап и шестой этап – разработка алгоритма и составление программы для ЭВМ. Два этих этапа творческий и трудно формализуемый процесс. В настоящее время при компьютерном математическом моделировании наиболее распространенными являются приемы объектно-ориентированного программирования.

Седьмой этап – после составления программы необходимо решить с ее помощью простейшую тестовую задачу (желательно, с заранее известным ответом) с целью устранения грубых ошибок. Это лишь начало процедуры тестирования, которую трудно описать формально исчерпывающим образом. По существу, тестирование может продолжаться долго и закончиться тогда, когда пользователь по своим профессиональным признакам сочтет программу верной.

Восьмой этап – численный эксперимент, при котором и выясняется, соответствует ли модель реальному объекту (процессу). Модель адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с их экспериментальными значениями с заданной степенью точности. В случае несоответствия модели реальному процессу необходимо вернуться к одному из предыдущих этапов.