Распределительный метод

Как и в симплекс-методе, улучшать полученное допустимое решение будем за счет перевода одной из базисных переменных в разряд свободных и одной из свободных переменных в разряд базисных. Количество свободных и количество базисных переменных при этом не меняются.

Процесс улучшения допустимого решения рассмотрим как продолжение примера 4 (п. 3.2). В полученном допустимом решении имеются две свободные переменные x₁₂ и х₂₁. Произвольно выберем переменную х₂₁ и увеличим значение этой переменной от нуля до единицы х₂₁=l (табл. 3.3.). При этом нарушаются балансы мощности по 1-му столбцу и 2-й строке.

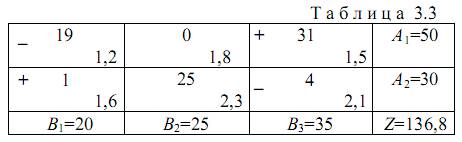
Для восстановления этих балансов уменьшим на единицу значения базисных переменных, входящих в 1-й столбец и 2-ю строку (х₁₁=19, х₂₃=4). При этом нарушаются балансы по 1-й строке и 3-му столбцу. Базисную переменную х₁₃, находящуюся на пересечении 1-й строки и 3-го столбца, увеличим на единицу (x₁₃=31). Балансы мощности по всем строкам и столбцам оказываются восстановленными.

В результате выполненных действий в транспортной матрице получен замкнутый цикл, вершины которого отмечены знаками "+" и "-". Начальная вершина цикла лежит в клетке свободной переменной х₂₁ которая переводится в базис. Все остальные вершины цикла лежат в клетках базисных переменных х₁₁, х₁₃и х₂₃. Знак "+" в вершине цикла соответствует увеличению переменной, знак "-" - ее уменьшению.

При увеличении на единицу свободной переменной изменение целевой функции определится как алгебраическая сумма удельных стоимостей, стоящих в вершинах цикла. Изменение целевой функции при увеличении на единицу свободной переменной х₂₁ составит

Видно, что при увеличении свободной переменной х₂₁ значение целевой функции уменьшается. Эту свободную переменную следует перевести в базис.

Совершенно аналогичные действия можно выполнить и для свободной переменной х₁₂. Несложно показать, что увеличение этой переменной на единицу даст увеличение целевой функции

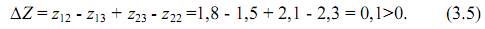
Поэтому свободную переменную х₁₂ не следует переводить в базис.

Итак, в базис переводится переменная x₂₁. В соответствии со знаками вершин цикла (табл. 3.3) при увеличении этой переменной в положительную сторону базисные переменные х₁₁ и х₂₃ будут уменьшаться, а базисная переменная x₁₃ будет увеличиваться.

Естественно, что первой достигнет нулевого значения и станет свободной переменная х₂₃, меньшая из базисных переменных в отрицательных вершинах цикла. Свободная переменная х₂₁ примет значение переменной х₂₃ и станет базисной. Базисные переменные х₁₁ и х₁₃ изменятся на величину переменной х₂₃ в соответствии со знаками в вершинах цикла.

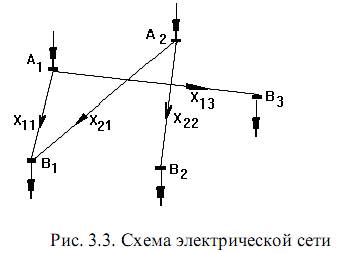
Получено новое допустимое решение (табл. 3.4 и рис. 3.3).

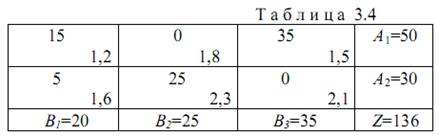
В этом новом решении

свободные переменные х₁₂=0, х₂₃=0;

базисные переменные х₁₁=15, х₁₃⁼35, х₂₁=5, х₂₂⁼25 е.м.; значение целевой функции

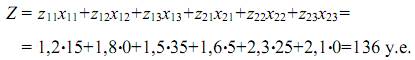
Видно, что значение целевой функции улучшилось по сравнению с предыдущим решением (136<137).

В новом решении строятся циклы пересчета и определяются изменения целевой функции DZ для каждой свободной переменной x₁₂ и х₂₃. Если для каждой свободной переменной изменение целевой функции DZ>0, то полученное решение будет оптимальным.