Теоретическое введение. В работе изучаются такие движения в механике, при которых существенна конечная протяженность тел – их нельзя рассматривать в данных условиях

Простейшим движением твердого тела является поступательное. Тело перемещается параллельно самому себе; все точки его имеют одинаковую скорость и описывают траектории одинаковой формы, только смещенные по отношению друг к другу. При этом кинетическая энергия равна:

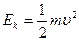(9.1)

где 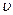– скорость тела, 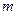– его полная масса.

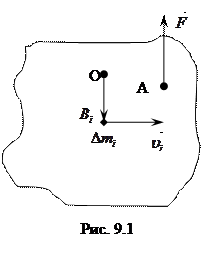
Другим простейшим видом движения твердого тела является вращение тела вокруг оси. Определим кинетическую энергию твердого тела, закрепленного на неподвижной оси, вокруг которой оно может свободно вращаться (рис.9.1); точка О – след этой оси. К одной из точек тела А приложена внешняя сила 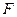. Мысленно разделим тело на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки. 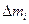– масса этого элемента, 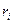– его расстояние до оси вращения. При вращении различные точки тела описывают окружности, лежащие в плоскостях, перпендикулярных оси вращения. Если за время 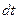тело поворачивается на угол 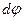, то путь 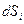, проходимый за это время какой-либо точкой тела 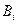, будет равен 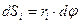. Разделив 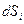на 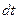, найдем скорость точки :

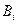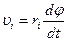(9.2)

Величина 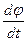одинакова для всех точек тела и представляет собой угловое перемещение тела за единицу времени. Она называется угловой скоростью тела .

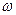Так что величины скоростей различных 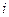-х элементов равны:

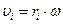(9.3)

Кинетическая энергия такого элемента по определению равна:

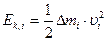(9.4)

Просуммировав эти энергии, получим полную кинетическую энергию вращающегося твердого тела:

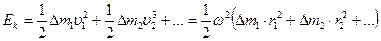(9.5)

Стоящая здесь в скобках сумма зависит от того, с каким именно твердым телом мы имеем дело (от его формы, размеров и распределения массы в нем), а также от того, как расположена в нем ось вращения. Эта величина, характеризующая твердое тело и выбранную ось вращения, называется моментом инерции относительно данной оси и обозначается буквой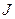

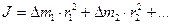(9.6)

Если твердое тело – сплошное, то его нужно разделить на бесконечно большое количество бесконечно малых частей. Суммирование в (9.6) заменяем интегрированием.

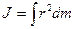. (9.7)

Так как 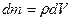( 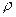– плотность тела), то вычисление момента инерции сводится к объемным интегралам:

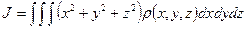(9.8)

Вычисление таких интегралов в общем случае представляет собой сложную задачу. Лишь для тел симметричной формы при однородном распределении массы по объему тела их моменты инерции определить достаточно просто, если ось вращения проходит через центр масс (шар, цилиндр, диск, стержень). Поэтому моменты инерции сложных тел проще определять экспериментально.

Таким образом, кинетическая энергия вращающегося тела может быть записана в виде:

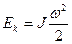(9.9)

Это выражение формально похоже на выражение для энергии поступательного движения (9.1), отличаясь от него тем, что вместо скорости 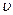стоит угловая скорость 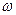, а вместо массы 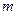- момент инерции 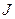. Так что при вращении момент инерции играет роль, аналогичную массе при поступательном движении.

Далее кинетическую энергию произвольно движущегося твердого тела можно представить в виде суммы поступательной и вращательной энергий, если ось вращения проходит через центр инерции тела. Тогда для кинетической энергии произвольно движущегося тела имеем:

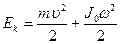, (9.10)

здесь первое слагаемое – кинетическая энергия поступательного движения, 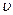- скорость перемещения центра инерции; второе слагаемое – кинетическая энергия вращения тела вокруг оси, проходящей через центр инерции. Индекс “0” у момента инерции именно это и означает.

Независимо от характера движения тел (поступательного или вращательного) для замкнутых систем справедлив закон сохранения механической энергии (суммы кинетической и потенциальной энергий), если между телами действуют только консервативные силы. Если в замкнутой системе тел действуют и не консервативные силы, например, силы трения, то изменение механической энергии системы равно работе неконсервативных сил:

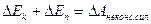(9.11)

В данной лабораторной работе используется именно этот закон. Необходимо еще дать определение работы при вращении твердого тела. Выражение для работы 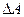при вращении твердого тела вокруг оси легко представить, если продолжить отмеченную аналогию между соотношениями динамики поступательного движения и динамики твердого тела: вместо линейной скорости 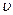– угловая скорость 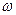; вместо массы 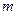– момент инерции 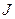; вместо силы 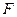– момент силы 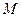, вместо пути 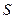– угол поворота 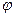. Тогда вместо соотношения 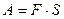, определяющего работу при поступательном движении, для вращательного движения имеем:

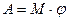(9.12)