Основы работы передачи

Окружное усилие в цепной передаче передается за счет сил давления зубьев ведущей звездочки на звенья цепи и затем давлением звеньев ведущей ветви на зубья ведомой звездочки.

В процессе работы ведущая ветвь цепи испытывает постоянную нагрузку S₁, которая состоит из полезной силы P и натяжения ведомой ветви S₂.

S₁ =Р + S₂

Натяжение S₂ можно определить из условия равновесия цепи (рис. 11.6). При этом вес (q) одного погонного метра цепи принимается для простоты как вес на длине, равной межосевому расстоянию (a_W). Стрела провисания – (f).

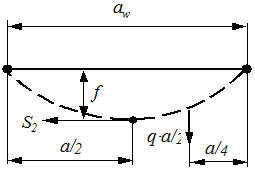
Рис. 11.8. Определение усилия натяжения цепи

Уравнение моментов

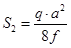
Обычно S₂ составляет менее 10 % от Р.

Обозначим

,

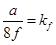где k_f – коэффициент провисания

и получим

S₂ = k_f·q·a.

Принимая f = 0,02·а, получим для горизонтальной передачи (Q = 0) k_f = 6, при Q ≤ 40°.

k_f = 4 и при Q > 40° k_f = 2, а при Q =90° k_f = 1,0.

Натяжение цепи от центробежной силы определяется и учитывается при V > 5 м/с.

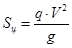
где V – скорость цепи, м/с

g = 9,81 м/с² – ускорение силы тяжести.

Каждое звено ведет цепь при повороте звездочки на один угловой шаг, а затем уступает место следующему звену. В связи с этим скорость цепи при равномерном ращении звездочки не постоянна. Она максимальна в положении звездочки, когда ее радиус, проведенный через шарнир, перпендикулярен ведущей ветви.

В произвольном угловом положении звездочки, когда ведущий шарнир повернут на угол α скорость цепи равна

V = ω₁·R₁·Cos α ;

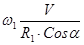
где ω₁ – постоянная угловая скорость ведущей звездочки;

R₁ – радиус начальной окружности.

Угол (α) изменяется в пределах от 0 до , поэтому и скорость цепи изменяется от V_max до .

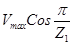Мгновенная угловая скорость ведомой звездочки равна

где R₂ – радиус начальной окружности ведомой звездочки

β – угол поворота шарнира, примыкающего к ведущей ветви по отношению к перпендикуляру на эту ветвь. Угол β изменяется от «0» до .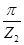

Мгновенное передаточное число равно

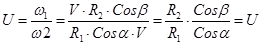
т.к. α ≠ const; β ≠ const, то и U ≠ const , чем больше Z₁ и Z₂, тем выше равномерность движения.