Словесный способ записи алгоритмов
При словесном способе записи алгоритма пользуются средствами обычного языка, математическими символами и выражениями. Последовательность действий часто оформляется в виде шагов, которые нумеруются. Достоинством этого способа является наличие возможности записать алгоритм с любой степенью детализации.
 Задача 2. Волк, коза и капуста. Исполнитель – Крестьянин. На берегу реки стоит крестьянин с лодкой, а рядом с ним – волк, коза и капуста. Крестьянин должен переправиться сам и перевезти волка, козу и капусту на другой берег. Однако в лодку, кроме крестьянина, помещается либо только волк, либо только коза, либо только капуста. Оставлять же волка с козой или козу с капустой без присмотра нельзя – волк может съесть козу, а коза – капусту. Напишите алгоритм переправы крестьянина, волка, козы и капусты с левого берега на правый.
Задача 2. Волк, коза и капуста. Исполнитель – Крестьянин. На берегу реки стоит крестьянин с лодкой, а рядом с ним – волк, коза и капуста. Крестьянин должен переправиться сам и перевезти волка, козу и капусту на другой берег. Однако в лодку, кроме крестьянина, помещается либо только волк, либо только коза, либо только капуста. Оставлять же волка с козой или козу с капустой без присмотра нельзя – волк может съесть козу, а коза – капусту. Напишите алгоритм переправы крестьянина, волка, козы и капусты с левого берега на правый.
Решение. Выберем для исполнения составляемого алгоритма исполнителя Крестьянина. Дадим строгое описание исполнителя: где работает Крестьянин, и какие команды он может исполнять. Крестьянин работает на переправе и в его распоряжении находится лодка. Опишем команды, которые научим выполнять Крестьянина: вправо коза; вправо волк; вправо капуста; влево коза; влево волк; влево капуста; вправо ничего; влево ничего. Рассмотрим как выполняет команду «вправо коза» Крестьянин. При выполнении этой команды Крестьянин совершит следующие действия: погрузит в лодку козу, перевезёт её на правый берег, выгрузит её там и остановится в ожидании команды. Аналогично выполняются другие команды.
Алгоритм:
| вправо коза; влево ничего; вправо волк; влево коза; | вправо капуста; влево ничего; вправо коза |
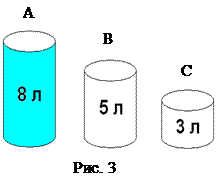 Задача 3.Переливание воды.Исполнитель – Водолей. На столе стоят три ёмкости воды разных размеров. В первую ёмкость вмещается 8 литров воды, во вторую – 5 литров воды, в третью – 3 литра воды. Первая ёмкость заполнена доверху водой, две другие ёмкости пустые. Напишите алгоритм получения в двух ёмкостях по 4 литра воды, чтобы затем залить воду по 4 литра в два аквариума; нельзя проливать ни капли воды на стол.
Задача 3.Переливание воды.Исполнитель – Водолей. На столе стоят три ёмкости воды разных размеров. В первую ёмкость вмещается 8 литров воды, во вторую – 5 литров воды, в третью – 3 литра воды. Первая ёмкость заполнена доверху водой, две другие ёмкости пустые. Напишите алгоритм получения в двух ёмкостях по 4 литра воды, чтобы затем залить воду по 4 литра в два аквариума; нельзя проливать ни капли воды на стол.
Решение. Выберем для исполнения составляемого алгоритма исполнителя Водолея. Дадим строгое описание Водолея: с чем работает Водолей, какие команды входят в его систему команд (СКИ). Водолей работает с тремя ёмкостями (8 л, 5 л, 3 л), обозначим ёмкости буквами А, В, С. Опишем команды, которые научим выполнять Водолея: перелей из А в В, перелей из А в С, перелей из В в А, перелей из В в С, перелей из С в А, перелей из С в В. Рассмотрим команду «перелей из А в В». Результат этой команды зависит от того, достаточно ли в ёмкости В места для всей воды из ёмкости А. Если да, то ёмкость А становится пустой, а в В оказывается столько воды, сколько было в А и В вместе до переливания. Если же места в В недостаточно, то В становится полной, а в А остается столько воды, сколько не поместилось в В. Аналогично выполняются Водолеем другие команды СКИ.
| Алгоритм | Таблица-протокол исполнения алгоритма | |||||
| Номер шага | Команда | Количество воды в емкостях | ||||
| А | В | С | ||||
| 1 шаг | Перелей из А в В | |||||
| 2 шаг | Перелей из В в С | Перелей из А в В | ||||
| 3 шаг | Перелей из С в А | Перелей из В в С | ||||
| 4 шаг | Перелей из В в С | Перелей из С в А | ||||
| 5 шаг | Перелей из А в В | Перелей из В в С | ||||
| 6 шаг | Перелей из В в С | Перелей из А в В | ||||
| 7 шаг | Перелей из С в А | Перелей из В в С | ||||
| Перелей из С в А |
Задача 4. Задача о перестановке четырех коней.Исполнитель – Конюх. Напишите алгоритм (для исполнителя Конюха) перестановки коней из начального положения в конечное (рис.4).
Конь перемещается за один ход либо на два поля по вертикали и одно поле по горизонтали, либо на два поля по горизонтали и одно по вертикали (буквой «Г»). Конь может перепрыгивать через стоящие на его пути другие фигуры, но может перемещаться (ходить) в нашей задаче только на свободные поля.
|
| ||||||||||||||||||||||||||||||||
| Начальное положение | Конечное положение |
Рис. 4
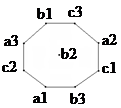
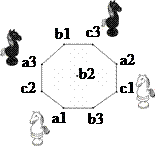
Решение. Каждой клетке доски сопоставим точку на плоскости, и если из одной клетки можно попасть в другую ходом коня, то соединим соответствующие точки линией, получим граф (рис. 5).
|  
|  
|
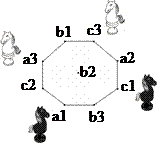
| Начальное положение | Конечное положение |
Рис.5
Начальная и конечная расстановки коней изображены на рисунке 5.
Написание алгоритма перестановки коней для исполнителя Конюха становится элементарной задачей.
Алгоритм перестановки коней
Действие, производимое исполнителем, – это одно перемещение какого-нибудь коня на доступную клетку поля. Запись действий формализуем: сначала обозначим поле, с которого надо переставить коня, потом нарисуем стрелку, а затем обозначим поле, на которое надо поставить коня. Один из возможных алгоритмов имеет вид:
| Шаги | Номер коня | Команда | Шаги | Номер коня | Команда |
| 1 шаг | a1→c2 | 9 шаг | a3→b1 | ||
| 2 шаг | c1→b3 | 10 шаг | a1→c2 | ||
| 3 шаг | c3→a2 | 11 шаг | c1→b3 | ||
| 4 шаг | a3→b1 | 12 шаг | c3→a2 | ||
| 5 шаг | c2→a3 | 13 шаг | b1→c3 | ||
| 6 шаг | b3→a1 | 14 шаг | c2→a3 | ||
| 7 шаг | a2→c1 | 15 шаг | b3→a1 | ||
| 8 шаг | b1→c3 | 16 шаг | a2→c1 |
Задача 5. Легкая пластинка. Исполнитель – Эксперт. Имеется 9 пластинок и двухчашечные весы без гирь. Одна из пластинок легче других, но по виду они одинаковые. Как с помощью двух взвешиваний найти более легкую пластинку? Напишите алгоритм определения легкой пластинки.
Решение. Определим исполнителя Эксперта. Эксперт работает на рабочем столе. На столе 9 пластинок, весы и две коробки (склад1, склад2). Эксперт умеет взвешивать пластинки, определять какая из чашек весов с пластинками легче, определять количество предметов, лежащих на столе, делить количество предметов на три равные группы, сравнивать количество предметов.
Алгоритм
1 шаг. Раздели все пластинки на рабочем столе на 3 равные группы.
2 шаг. Положи две группы пластинок на весы, а третью в склад1.
3 шаг. Сравни чаши весов.
4 шаг. Если правая чаша весов легче, то положи на рабочий стол пластинки из правой чаши, а пластинки из левой чаши и из склада1 положи в склад2 и иди на шаг 7, иначе иди на шаг 5.
5 шаг. Если левая чаша весов легче, то положи на рабочий стол пластинки из левой чаши, а пластинки из правой чаши и из склада1 положи в склад2 и иди на шаг 7, иначе иди на шаг 6.
6 шаг. Положи пластинки из левой чаши и правой в склад2 (чаши уравновешены), на рабочий стол положи пластинки из склада1 и иди на шаг 7.
7 шаг. Сосчитай пластинки на рабочем столе.
8 шаг. Если на столе более одной пластинки иди на шаг 1, иначе на шаг 9.
9 шаг. Закончи алгоритм определения легкой пластинки (она лежит на столе).
Задача 6. Деление. Исполнитель – Вычислитель. Составьте алгоритм вычисления остатка r от деления m на n, где m и n – натуральные числа.
Решение. Перечислим команды системы команд исполнителя: сравни два натуральных числа, найди разность двух натуральных чисел, присвой значение переменной.
Исходные данные – натуральные числа m и n.
Алгоритм
Шаг 1. Сравни m с n: если m<n, то перейди к шагу 2, в противном случае перейди к шагу 3.
Шаг 2. Прими r равным m. Перейди к шагу 4.
Шаг 3. Замени значение m значением m-n. Перейди к шагу 1.
Шаг 4. Закончи процесс вычисления.
Легко понять, что расчленение на шаги обусловлено элементарными операциями, которые мы выбираем для решения задачи.
Применим указанный алгоритм к исходным данным m=18 и n=7.
Алгоритм начинается с шага 1, далее шаги выполняются в естественном порядке, если нет специальных указаний о порядке следования (в рассматриваемом случае такие указания есть).
Шаг 1. Установи, что 18<7 – ложное неравенство; следуя указаниям этого шага, перейди к шагу 3.
Шаг 3. Прими m равным 18-7, т.е. 11. Перейди к шагу 1.
Шаг 1. Установи, что 11<7 – ложное неравенство; следуя указаниям этого шага, перейди к шагу 3.
Шаг 3. Прими m равным 11-7, т.е. 4. Перейди к шагу 1.
Шаг 1. Установи, что 4<7 – верное неравенство. Перейди к шагу 2.
Шаг 2. Прими r равным 4. Перейди к шагу 4.
Шаг 4. Закончи процесс вычисления, взяв r равным 4.
Задача 7. Буква в слове. Исполнитель – Буквоед. Пусть задано слово в алфавите русского языка. Относительно произвольной буквы этого алфавита требуется решить вопрос о том, входит ли она в это слово, и если входит, указать номер позиции первого вхождения этой буквы в слово. Напишите алгоритм решения задачи, учитывая, что при его выполнении Буквоед использует следующие элементарные операции: сравни две буквы, присвой значение переменной, сравни значения переменных, зафиксируй ответ, увеличь значение переменной на единицу.
Решение. Пусть a1a2…an – обозначение слова, состоящего из n букв русского алфавита, а b – обозначение буквы, относительно которой требуется установить, входит она в слово или нет; i – номер позиции, занимаемой буквой ai в слове, где i изменяется от 1 до n.
Алгоритм решения задачи может быть таким:
Шаг 1. Положи i равным 1.
Шаг 2. Сравни b c ai. Если b совпадает с ai, то перейди к шагу 5, иначе – к шагу 3.
Шаг 3. Увеличь i на единицу.
Шаг 4. Сравни i с n. Если i≤n, то перейти к шагу 2, в противном случае перейди к шагу 6.
Шаг 5. Зафиксируй ответ: буква b входит в i-ю позицию слова. Перейди к шагу 7.
Шаг 6. Зафиксируй ответ: буква b не входит в слово.
Шаг 7. Процесс закончи.
Применим исходный алгоритм к слову «алгебра» и букве «г».
Данными являются: a1=а, a2=л, a3= г, a4=е, a5=б, a6=р, a7=а, b= г, n=7.
Каждая буква в слове занимает определенную позицию, которая указывается номером i, где i изменяется от 1 до 7.
Шаг 1. Положи i = 1.
Шаг 2. Сравни «г» с буквой, занимающей в слове «алгебра» первую позицию; «г» отлична от «а», перейди к шагу 3.
Шаг 3. Увеличь i на 1, i = 2. Перейди к шагу 4.
Шаг 4. Сравни i = 2 с 7. 2≤7 – верное неравенство, перейди к шагу 2.
Шаг 2. Сравни «г» с a2, т.е. с «л»; «г» отлична от «л», перейди к шагу 3.
Шаг 3. Увеличь i на 1, i = 3. Перейди к шагу 4.
Шаг 4. Сравни i = 3 с 7. 3≤7 – верное неравенство, перейди к шагу 2.
Шаг 2. Сравни «г» с a3, т.е. с «г»; «г» совпадает с a3, перейди к шагу 5.
Шаг 5. Зафиксируй ответ. Буква «г» входит в третью позицию данного слова. Перейди к шагу 7.
Шаг 7. Процесс закончи.
 Задача 8.Решето Эратосфена. ИсполнительВычислитель.Напишите алгоритм решения задачи. Из первых n натуральных чисел найдите все простые[3] числа. Для решения задачи примените метод, предложенный греческим математиком Эратосфеном (276-194 гг. до н.э.). Сущность метода – вычеркивается число 1, затем все числа, кратные 2 (кроме 2), затем кратные 3 (кроме 3) и т.д. Таким образом надо вычеркнуть все числа, кратные простым числам: p1 = 2, p2 = 3, p3 = 5, …,
Задача 8.Решето Эратосфена. ИсполнительВычислитель.Напишите алгоритм решения задачи. Из первых n натуральных чисел найдите все простые[3] числа. Для решения задачи примените метод, предложенный греческим математиком Эратосфеном (276-194 гг. до н.э.). Сущность метода – вычеркивается число 1, затем все числа, кратные 2 (кроме 2), затем кратные 3 (кроме 3) и т.д. Таким образом надо вычеркнуть все числа, кратные простым числам: p1 = 2, p2 = 3, p3 = 5, …, 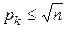 .
.
Решение. Перечислим команды СКИ: найди неотмеченное число, отмеченным числом будем считать подчёркнутое число; определи кратность двух чисел; вычеркни (перечеркни) найденное кратное число.
Исходные данные – натуральное число n.
Алгоритм
Выполните последовательно действия (команды) для n натуральных чисел, которые меньше или равны 23.
Шаг 1. Выпиши все натуральные числа от 1 до 23, вычеркни 1.
Шаг 2. Подчеркни наименьшее натуральное число из неотмеченных, из неподчёркнутых и неперечёркнутых чисел.
Шаг 3. Вычеркни все числа, кратные подчёркнутому числу на предыдущем шаге.
Шаг 4. Проверь, имеются ли еще какие-нибудь неотмеченные числа, неподчёркнутые и неперечёркнутые, если нет, то задача решена: все подчеркнутые числа – это простые числа, иди на шаг 5. Если же имеются еще неотмеченные числа, перейди на выполнение шага 2.
Шаг 5. Процесс закончи.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23
Дата добавления: 2015-01-26; просмотров: 3839;







