Шкала пропорциональных оценок
Здесь мы имеем дело с идеальной или абсолютной метрической шкалой, напоминающей шкалу равных интервалов, но с одним преимуществом: отсчет в этой шкале начинается не с произвольной точки, а с экспериментально установленного нулевого пункта. Для таких шкал применимы решительно все операции с числами, так как можно определить, на сколько или во сколько данный пункт на шкале превышает другой. Подобные шкалы приняты в точных науках, где нулевой пункт (точка отсчета — из чего и происходит название "точные науки") экспериментально зафиксирован.
Идеальные метрические шкалы успешно применяются для измерения некоторых физиологических и психических свойств человека. Точка отсчета определяется в этих случаях как порог восприятия и порог насыщения. Известно, например, что существует среднестатистический порог восприятия звуковых колебаний. То же относится и к некоторым психическим реакциям людей (например, порог различения сходных фигур).
В социологии шкалы такого рода имеют весьма ограниченное применение. Ими пользуются для измерения протяженностей во времени и пространстве, для отсчета натуральных единиц (денежных единиц, продуктов деятельности» поступков). Во всех этих случаях нулевой пункт четко фиксируется.
Что касается измерения качественных свойств социальных явлений, поиск нулевого пункта как точки отсчета заведомо обречен на неудачу. Как правило, социальные процессы и характеристики варьируют от ситуации к ситуации столь сильно, что нулевой пункт может быть установлен только как среднестатистическая величина в большой массе событий.
Операции с числами, как уже говорилось, для идеальных шкал не имеют никаких ограничений. Можно использовать все доступные математике операции с натуральными числами.
Теперь, ознакомившись с различными типами шкал, мы могли бы заметить, что собственно измерение начинается как будто бы с введения обоснованной метрики в шкалах равных интервалов (типа шкал Гуттмана) и в шкалах пропорциональных оценок. Номинальные упорядоченные шкалы предполагают ранжирование объектов (свойств), а простые номинальные шкалы есть лишь их классификация.
Однако классификация в номинальной шкале, а тем более ранжирование объектов — это тоже измерение, так как с помощью данных процедур мы фиксируем меру, протяженность, континуум. В социологии, а также в психологии приходится, как правило, довольствоваться такими элементарными способами первичного измерения. Но этого, в общем, достаточно для того, чтобы фиксировать тенденцию изучаемого социального процесса. На большее социолог не претендует, да вряд ли и должен претендовать.
3. ПОИСК ОДНОНАПРАВЛЕННОГО КОНТИНУУМА В ШКАЛАХ ГУТТМАНА (УПОРЯДОЧЕННАЯ НОМИНАЛЬНАЯ ШКАЛА)
Поиск одномерного континуума свойств некоторой неявной (латентной) характеристики по внешним ее проявлениям — довольно сложная задача. Один из вариантов ее решения предложил Луи Гуттман [64]. Шкала Гуттмана предназначена для измерения установок, т. е. субъективного отношения к объекту, и обладает двумя важными достоинствами: кумулятивностью и репродуктивностью.
Такие арифметические действия, как сложение, умножение и возведение в степень, ранжированы по кумулятивной, т. е. накопительной, шкале. Тот, кто умеет возводить в степень, непременно умеет умножать и складывать. Но кто умеет складывать, вовсе не обязательно умеет умножать (не говоря о возведении в степень). С принципом кумулятив-ности связана и реп род уктивн ость. Зная максимальные математические возможности некоего человека, можно надежно предсказать его возможности в менее ответственном испытании, причем все это относится к одному и только одному параметру. В нашем случае — это накопительные операции с натуральными числами (а не что-то иное).
Рассмотрим вымышленный пример построения шкало-граммы для измерения социальных установок людей по поводу перехода на новую систему организации труда. Предлагая опрашиваемым серию суждений, мы просим высказать свое отношение к каждому из них. При этом несогласие с суждением, в котором критикуется новая система, наряду с согласием по поводу благоприятствующих ей мнений оценивается как положительное отношение и дает респонденту 1 балл в суммарном показателе.
В следующем списке согласие с суждениями 1, 2, 5, 6 и несогласие с суждениями, 3, 4, 7, 8 свидетельствуют о благоприятном отношении к новой системе организации (обратите внимание: численность позитивных и негативных Утверждений должна быть равной).
Список исходных суждений для построения шкалограммы
1. Новая система организации, несомненно, способствует повышению производительности труда. ----Согласен (1)----Не согласен (0)
2. В целом эта система лучше той, что применялась прежде. ----Согласен (1)----Не согласен (0)
3. Некоторые стороны новой системы организации плохо продуманы.
----Согласен (0)----Не согласен (1)
4. Как и любая другая система организации, новая система имеет немало минусов.
----Согласен (0)----Не согласен (1)
5. Новая система удачно сочетает материальное и моральное стимулирование работников.
----Согласен (1)----Не согласен (0)
6. Доводы в пользу новой системы очень убедительны. ----Согласен (1)----Не согласен (0)
7. В прежней системе было немало хорошего, что утрачено п новой организации.
----Согласен (0)----Не согласен (1)
8. Преимущества новой системы организации совершенно не ясны.
----Согласен (0)----Не согласен (1)
Если приписать каждому положительному ответу 1 балл и каждому отрицательному — нулевой, то человек, максимально благоприятно оценивающий новую систему организации, получит 8 баллов, а противник этой системы — 0 баллов. Остальные распределяются в промежутках между двумя полюсами шкалограммы.
Процедура отработки шкалограммы состоит в следующем [353. С. 143—157].
(1) Отбирается экспериментальная группа, которой предлагают высказаться по поводу суждений, предположительно образующих континуум. В составе группы должны быть представители обследуемой категории населения. Численность группы — около 50 человек (в нашем примере для простоты возьмем 15 человек).
(2) Высший балл по шкале определяется суммированием оценок по каждому ответу. В нашем примере для каждого суждения возможны оценки 1 или 0. В более сложных шкалах предлагается высказать полное или частичное согласие (несогласие) с каждым суждением:
4. Совершенно согласен.
3. Согласен.
2, Не знаю, не могу ответить.
1. Не согласен.
0. Категорически не согласен.
В этом случае высшая оценка в шкалограмме из 8 суждений составит 8x4=32, а низшая, как и прежде, = 0.
(3) Данные опроса экспериментальной группы располагаются в матрицу так, чтобы упорядочить опрошенных по числу набранных баллов от высшего к низшему (схема 12).
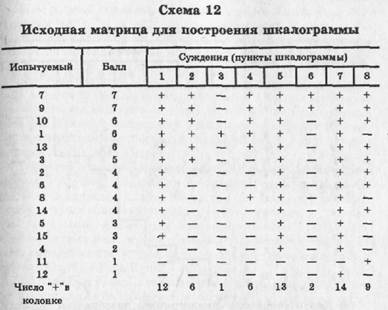
Знак "+" означает благожелательное отношение к объекту оценивания, "—** означает неблагожелательное отношение.
Анализируя полученную шкалограмму, видим, что она весьма близка к идеальному варианту. Например, балл 3 для суждения № 5 определенно связан с положительным отношением к новой системе по суждениям 1, 5 и 7; балл 6 по суждению № 10 означает благоприятное отношение по пунктам 1, 2, 4, 5, 7 и 8. Не очень удачны пункты 3 и 7. С суждением №3 ("Некоторые стороны новой системы организации плохо продуманы") почти никто не согласен, что дает каждому по дополнительному баллу. Зато с пунктом 7 ("В прежней системе было немало хорошего, что утрачено в новой организации") подавляющее большинство согласно, и это отнимает у них по баллу. Оба пункта, следовательно, плохо дифференцируют опрошенных. Наиболее удачны суждения №2 и 4, которые делят респондентов на сторонников и противников новой системы организации.

(4) Для очевидности шкалограммы преобразуем таблицу так, чтобы получить идеальную "лесенку" (схема 13).
Идеальная шкалограмма предполагает, что ответ на один из вопросов должен повлечь за собой определенный ответ на следующий за ним по нисходящей ветви. Значит, первая задача состоит в том, чтобы выяснить, действительно ли ответы на эти вопросы образуют одномерный континуум.
Число лиц в экспериментальной группе достигает 50-100 человек, а число пунктов также достаточно велико. Кроме того, на каждый вопрос можно было бы дать пять ответов (от "совершенно согласен" до "совершенно не согласен"). Поэтому вращение рядов шкалограммы — утомительная операция. Гуттман, не имея компьютера, разработал несколько технических приемов. Один из них: деревянная доска, на которой передвигаются цветные фишки, соответствующие позитивным— негативным ответам. Конечно, при современных возможностях использовать компьютер все эти сложные перестановки максимально упрощаются (в SPSS для этого есть специальная программа).
После упорядочения респондентов, как показано в схеме 12, упорядочиваются пункты от максимума к минимуму благожелательных ответов. Внутри пункта производится сортировка субъектов так, чтобы набравшие максимум баллов располагались выше тех, кто набрал следующее за ними число баллов.
При ручной сортировке в карточку респондента заносятся ответы "за" и "против" каждого пункта информации, а также, общее число набранных баллов. Первая сортировка производится по колонке № 1 на всю выборку, затем — по остальным колонкам, т. е. вопросам.
Так определяется порядок вопросов в матрице от набравшего максимум до набравшего минимум благожелательных ответов. Вторая сортировка — внутри данной колонки ранжируются субъекты, набравшие максимум—минимум баллов. Составляется матрица, которую анализируем с точки зрения наличия континуума в ответах.
Вернемся к нашей шкалограмме. На схеме 13 видно, что имеется 6 случаев отклонения от идеального распределения: три благоприятных суждения выпали в "запретную" зону справа и три неблагоприятных суждения выпали в "запретную" зону слева. Используем пример с умением считать: перед нами тот случай, когда умеющий умножать почему-то не умеет складывать, а не умеющий умножать умеет возводить в степень. Иными словами, это — парадокс.
(5) Идеальную шкалограмму мы не получили. Но это вообще маловероятно. Следует стремиться к некоторому оптимальному варианту. Такой вариант задается числом допустимых отклонений в ответах экспериментальной группы. Подсчет допустимого числа отклонений производится путем исчисления коэффициента репродуктивности шкалограммы:
R = 1 – n \ KN
где R — коэффициент репродуктивности, К — число пунктов (в нашем случае = 8), по которым следует дать ответ, N — число испытуемых (в нашем случае =15), n — число ошибочных ответов, которые располагаются справа или слева от идеальной вертикали.
Коэффициент желательной репродуктивности задается исследователем как надежный интервал допустимой ошибки. Желательно получить не более 10% ошибочных ответов. Тогда коэффициент репродуктивности должен выражаться числом 0,90. Число допустимых ошибок подсчитываем, преобразуя формулу:
п = (1 - R)(KN).
В нашем примере для R=0,90 при 8 суждениях и 15 испытуемых число допустимых ошибок составит (1 — — 0,90)х(8х15)=12, т.е. существенно меньше, чем оказалось в реальности. Фактический коэффициент репродуктивности нашей шкалы достаточно высок и равен 0,95.
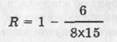
Можно повысить этот коэффициент до 0,98, если убрать суждение № 8, по которому имеются три ответа, отклоняющиеся от идеального континуума. Тогда:
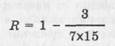
В случае, если на каждое суждение предполагается ответ по шкале в пять пунктов (4 = "совершенно согласен" ... О = "совершенно не согласен"), коэффициент репродуктивности может быть улучшен и за счет выбрасывания суждений, дающих много отклоняющихся ответов, и за счет укрупнения дробной шкалы согласия—несогласия с суждением.
(6) Шкала с коэффициентом репродуктивности не менее 0,90 готова. В массовом обследовании все пункты шкалы тасуются случайным образом. Ранг каждого опрашиваемого определяется по сумме набранных баллов.
Данные, полученные на группу, можно усреднить, подсчитав среднеарифметический ранг для этой категории лиц и сравнивая его с аналогичным средним показателем для другой категории. В нашем примере было бы интересно знать расхождение в оценках нововведений на государственных и частных предприятиях, руководителей и рядовых сотрудников.
Дата добавления: 2015-01-24; просмотров: 1310;
