Кинематика клапанов кривошипного насоса

На рис. 9.4 совмещены диаграммы движения всасывающего (ВК) и нагнетательного (НК) клапанов с развернутой индикаторной диаграммой. Начало движения каждого клапана сдвинуто относительно мертвого положения поршня на некоторый угол (j₁, j₂).

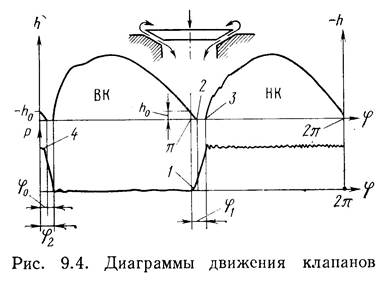Рассмотрим условия открытия нагнетательного клапана. В начале хода поршня ВК продолжает опускаться, при этом жидкость выталкивается из камеры в отверстие седла. Непосредственно перед посадкой клапана под его опорной поверхностью образуется прослойка жидкости, вытесняемой из клапанной щели в обе стороны (см. рис. 9.4). Поскольку эта прослойка оказывает движению клапана сопротивление, то давление в рабочей камере начинает возрастать еще до полной посадки всасывающего клапана (точки 1 и 2).

Интенсивность нарастания давления зависит от упругости перекачиваемой жидкости и податливости стенок рабочей камеры. Открытие НК (точка 3)происходит в момент, когда давление в камере несколько превысит давление жидкости над клапаном. Если противодавление невысокое, то этот момент может совпадать с моментом посадки ВК и даже опережать его.

Аналогичные события возникают в начале всасывания жидкости с тем отличием, что в камере происходит спад давления. Начало спада (точка 4)предваряет закрытие НК, а всасывающий клапан открывается в фазе j₂.

Хотя оба клапана конструктивно одинаковые, открываются они с различным опозданием во времени, что объясняется различием в объемах и в газосодержании сжимаемой и расширяющейся жидкости, а также влиянием конечной длины шатуна на скорость поршня.

Основные расчетные формулы.

Введем следующие обозначения (применительно к плоскому тарельчатому клапану):

h — высота подъема клапана; 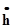— скорость клапана ( 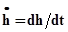); f_к — площадь тарелки (f_к = pd²/4); f_с — площадь сечения отверстия в седле; l — периметр тарелки; с — средняя скорость истечения из щели клапана; с_с — средняя скорость в седле, Q,Q_cp — текущий и средний расходы жидкости через клапан.

Уравнение сплошности потока (формула Вестфаля):

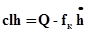, (9.2)

Если клапан опускается, то члены в правой части уравнения суммируются. В момент, когда h=0, скорость сне может быть бесконечно большой; поэтому

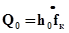(9.3)

причем расход в седле изменяется по закону

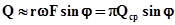. (9.4)

Перемещение и скорость подъема нагнетательного клапана условимся считать отрицательными, а всасывающего — положительными. Из формулы Вестфаля скорость истечения

.

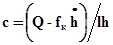В момент посадки это выражение становится неопределенным. Раскроем неопределенность по правилу Лопиталя:

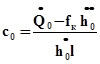(9.5)

В мертвой точке поршня скорость опускания клапана практически постоянна ( 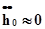). Подставив в (9.5) значения Q₀из (9.4) и 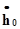из (9.3), получим угол поворота кривошипа, соответствующий времени запаздывания посадки клапана:

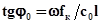. (9.6)

Скорость посадки клапана определим из (9.3) с учетом того, что при малых углах sinj » tgj:

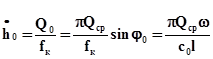. (9.7)

Приняв j_o = wt_o » tg j_o, вычислим высоту запаздывания посадки клапана:

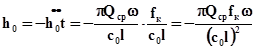. (9.8)

Для определения скорости с_o рассмотрим гидродинамическую силу Q, действующую на тарелку клапана. Эта сила зависит от геометрических очертаний потока, т. е. от формы и соотношений размеров тарелки, седла, клапанной камеры и высоты поднятия клапана над седлом. В геометрически подобных системах, характеризуемых определенным отношением h/d, сила Qзависит от плотности и вязкости жидкости, характерной площади (например, сечения отверстия в седле) и двух скоростей, характеризующих так называемый поток замещения с расходом жидкости 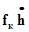и поток в седле с расходом Q(см. формулу 9.2). Две скорости необходимы потому, что поле скоростей, а следовательно, и давлений жидкости на тарелку при одной и той же скорости с могут быть различными в зависимости от соотношения интенсивности указанных потоков. Таким образом,

Q = f (r, n, f_c, с, с_с).

Эта связь выявляется только опытным путем. Результаты опытов представляются в виде графиков зависимости между следующими критериями:

1) коэффициентом истечения m₁ или коэффициентом обтекания z₁:

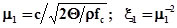; (9.9)

2) критерием Рейнольдса ( 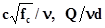и др.);

3) соотношением скоростей или расходов жидкости ( 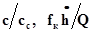и др.);

4) относительной высотой подъема клапана (h/d, hl/f_ки др.).

Поскольку клапан садится с постоянной скоростью и силы инерции отсутствуют, то равенство сил, действующих на клапан, имеет вид

Q_o=G_ж+R_o (9.10)

где G_ж — сила тяжести клапана в жидкости; R_o— натяжение пружины в нижнем положении клапана.

Из (9.9) и (9.10) получим

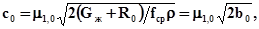(9.11)

где b_o— так называемая нагрузка клапана при h = 0.

Максимальную высоту подъема клапана вычисляем из (9.2) при условии 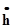= 0, приняв приближенно sin j = 1:

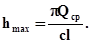(9.12)

Определение скорости с связано с некоторыми трудностями, так как неизвестно ускорение клапана. Обычно силой инерции клапана пренебрегают и вычисляют с по формуле (9.11) заменяя m_1,0 и b_o на m₁ и b,соответствующие максимальной высоте подъема клапана.