Закон распределения Пуассона
Распределение Пуассона играет особую роль в теории надежности, поскольку оно описывает закономерность появления случайных отказов в сложных системах. Этот закон нашел широкое применение при определении вероятности появления и восстановления отказов.
Случайная величина Х распределена по закону Пуассона, если вероятность того, что эта величина примет определенное значение т, выражается формулой
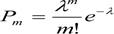 (1)
(1)
где λ— параметр распределения (некоторая положительная величина); m=0, 1. 2, ....
Математическое ожидание и дисперсия случайной величины Х для закона Пуассона равны параметру распределения λ:
Mx=Dx=λ (2)
Распределение Пуассона является однопараметрическим с параметром λ.
Пример 1.В ремонтную мастерскую по обслуживанию телевизоров поступают заявки со средней плотностью 5 шт. в течение рабочей смены за 10ч. Считая, что число заявок на любом отрезке времени распределено по закону Пуассона, найти вероятность того, что за 2 ч рабочей смены поступят две заявки.
Решение. Среднее число заявок за 2 ч равно λ=2*5/10=1.
Применяя формулу (3.1), найдем вероятность поступления двух заявок
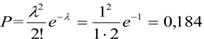
Дата добавления: 2015-01-21; просмотров: 1317;
