Количественные показатели риска

Количественно риск может быть определен как частота (размеренность - обратное время) реализации опасности.

Изучение статистических данных позволяет выявить частоту возникновения опасных событий. Однако серьезность событий (даже внутри одного класса аварий) может значительно изменяться от события к событию; тогда возникает необходимость введения категорий событий (например, события с тяжелыми, средними или легкими последствиями) и рассмотрения частоты каждой из таких категорий. Последнее достигается приписыванию каждому классу или подклассу показателя риска (числа событий за определенный период времени, деленный на длительность этого периода), имеющего размеренность обратного времени. Этот показатель иногда рассматривается как мера “вероятности” возникновения события. Следует рассмотреть замечание, сделанное по этому поводу редакторами перевода , смысл которого состоит в том, что наиболее естественно интерпретировать вводимый показатель в рамках некоторой математической модели, в данном случае - вероятностной, поскольку рассматриваются случайные явления. Например, можно характеризовать явление случайной величиной - обозначим ее z - числом случаев возникновения события (реализации явления) за определенный период времени Т, например за год. Хорошо известно, что математическое ожидание Мz случайной величины z - это среднее (ожидаемое) число случаев возникновения события за год или частота возникновения события. Тогда в соответствии с принятой в математической статистике терминологией число событий (которое берется из статистических данных) - это выборка, отношение числа событий к длительности периода наблюдения - статистика, являющаяся, очевидно, несмещенной и состоятельной оценкой математического ожидания Мz, или частоты возникновения событий. Если считать распределение случайной величины z, например пуассоновским, т.е. если положить 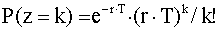, где r - константа, то возможно оценить условия, когда вводимый показатель можно считать вероятностью. В самом деле, для пуассоновского распределения Мz = r •T. С другой стороны, для пуассоновского распределения вероятность того, что за время Т случится не менее одного события, равна 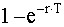. Поэтому только для очень малых частот возникновения события можно интерпретировать вводимый показатель как вероятность возникновения за время Т хотя бы одного события.

Необходимо, однако, отметить, что вводимый таким способом показатель не является вероятностью в точном, математическом смысле этого слова. Вероятностью (события в конечной схеме при классическом определении) называется отношение мощности множества элементарных исходов, составляющих это событие, к мощности всего множества элементарных исходов. Вероятность события - это действительное число, лежащее в интервале 0-1. Количественно риск может быть определен, как вероятность Р возникновения события В при наступлении события А (безразмерная величина, лежащая в пределах 0-1).

Поскольку реализация опасности явление случайное, риск опасности (как бы ни определять его - как частоту или вероятность) есть числовая характеристика соответствующей случайной величины, используемой для описания данной опасности. В качестве простейшего примера возможного формального подхода рассмотрим случайную величину s - длительность периода безаварийной работы промышленного предприятия, областью определения которой служит множество режимов эксплуатации за произвольное (возможно, бесконечное) время. Оказывается возможным явно вычислить функцию распределения этой величины F_s(t) = P(s£t), предположив ее независимость от предыстории функционирования промышленного предприятия (такое предположение является наиболее оптимистичным в отношении уровня безопасности). Хорошо известно, что существует единственное решение, удовлетворяющее сформулированному условию: F_s(t)= для t>0; F_s(t)=0 для t<0, где q>0 - постоянная; это так называемое показательное распределение. Математическое ожидание Мs случайной величины s есть Мs = 1/q, что позволяет интерпретировать параметр q как среднюю (ожидаемую) частоту аварий или риск аварий в смысле обсуждаемого определения. Вероятность аварий р_т за период времени, не превосходящий Т, определяется, очевидно, как р_т=Р(s£T) = . 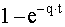Отметим, что всегда р_т<qT, поэтому неверно часто высказываемое утверждение, что для аварии, риск которой равен 1/Т, она обязательно случится за период Т (вероятность такого события равна 1-е^-1 , т.е. приблизительно 0,632). Более того, даже в этом простейшем случае показательного распределения было бы неверно утверждать, что вероятность аварии р_т за период времени, меньший или равный Т, определяется, как произведение частоты аварии p на этот период Т. Имеет место лишь приблизительное равенство в случае малых рисков, т.е. редких аварий. Однако, функциональная зависимость между вероятностью аварий и частотой ее возникновения (для фиксированного распределения) существует.

Последствие Y в виде нежелательного события или ущерба может в соответствии со своей величиной описываться своими специфическими параметрами. Диапазон при этом может быть весьма широк - от экономических до этических ценностей и человеческих жертв.

Мерой возможности наступления риска служит вероятность его наступления Р. Отсюда следует:R=Y×P.

Величина риска определяется как произведение величины нежелательного события на вероятность его наступления, т. е. как математическое ожидание величины нежелательных последствий.

Множества исходных причин развития риска можно записать в виде формулы:

R=P₁P₂P₃P₄, где R - риск, т.е. вероятность нанесения определенного ущерба;

Р₁ - вероятность возникновения события или явления, обусловливающего формирование и действие опасных факторов;

Р₂ - вероятность формирования определенных уровней физических полей, ударных нагрузок, полей концентрации вредных веществ, воздействующих на людей и другие объекты;

Р₃ - вероятность того, что указанные уровни полей и нагрузок приведут к определенному ущербу;

Р₄ - вероятность отказа средств защиты.

Мы узнали, что количественная мера риска может выражаться не только вероятностной величиной. Риск иногда интерпретируют как математическое ожидание ущерба, возникающего при реализации опасностей.

При определении математического ожидания величины ущерба представляется целесообразным принимать во внимание все возможные виды опасных происшествий для данного объекта и оценку риска производить по сумме произведений вероятностей указанных событий на соответствующие ущербы. В этом случае справедлива следующая зависимость:

,
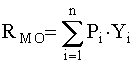где R_{М О} - уровень риска, выраженный через математическое ожидание ущерба;

Р_i - вероятность возникновения опасного события i-го класса;

Y_i - величина ущерба при i-ом событий.

Понятие “риск” - атрибут научного аппарата многих технических, экономических, общественных и естественных наук. У каждого из них свой предмет, свой аспект, а потому в определении меры риска в безопасности выделяют социальные, профессиональные, экологические, техногенные, медикобиологические, военные и др. опасности. Таким образом, риск - мера вполне определенных опасностей.

На рисунке 2. дан обзор ситуаций с риском возникновения соответствующих нежелательных событий и приведены их измерения.

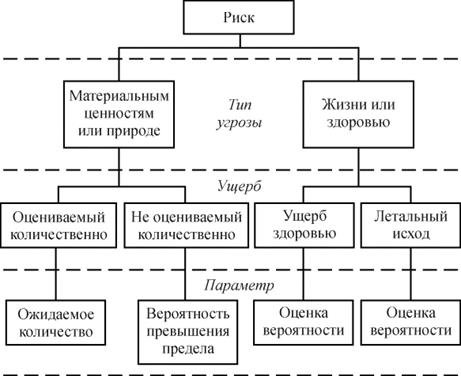
Рис. 2. Обзор ситуаций риска