Методы оценки инвестиций
Общие положения по экономической оценке инвестиционных проектов
5.2.1.1. Роль экономической оценки при выборе инвестиционных проектов [19]
Экономическая оценка инвестиционных проектов занимает центральное место в процессе обоснования и выбора возможных вариантов вложения средств в операции с реальными активами. При всех прочих благоприятных характеристиках проекта он никогда не будет принят к реализации, если не обеспечит:
· возмещение вложенных средств за счет доходов от реализации товаров или услуг;
· получение прибыли, обеспечивающей рентабельность инвестиций не ниже желательного для предприятия уровня;
· окупаемости инвестиций в пределах срока, приемлемого для предприятия.
Определение реальности достижения именно таких результатов инвестиционной деятельности и является ключевой задачей оценки финансово-экономических параметров любого проекта вложения средств в реальные активы.
Проведение такой оценки всегда является достаточно сложной задачей, что объясняется рядом факторов:
во-первых, инвестиционные расходы могут осуществляться либо разово, либо неоднократно на протяжении достаточно длительного периода времени (иногда до нескольких лет);
во-вторых, длителен и процесс получения результатов от реализации инвестиционных проектов (во всяком случае, он превышает один год);
в-третьих, осуществление длительных операций приводит к росту неопределенности при оценке всех аспектов инвестиций и к риску ошибки.
Именно наличие этих факторов породило необходимость создания специальных методов оценки инвестиционных проектов, позволяющих принимать достаточно обоснованные решения с минимально возможным уровнем погрешности (хотя абсолютно достоверного решения при оценке инвестиционных проектов, конечно же, быть не может).
5.2.1.2. Стоимость денег во времени. Дисконтирование [1, 19]
Одной из основных причин возникновения специальных методов оценки инвестиционных проектов является неодинаковая ценность денежных средств во времени.
В наиболее общем виде смысл понятия «стоимость денег во времени» может быть выражен фразой - рубль, имеющийся в распоряжении сегодня, и рубль, ожидаемый к получению в некотором будущем, не равны, а именно: первый имеет большую ценность по сравнению со вторым по двум причинам.
Первой причиной является обесценивание денег с течением времени из-за инфляции.
Вторая причина связана с обращением денежных средств. Рубль, вложенный в любого рода коммерческие операции (включая и простое помещение его на депозит в банке), способен через некоторое время превратиться в большую сумму за счет полученного с его помощью дохода.
Эта истина является аксиомой финансовых операций и предопределяет весь механизм экономического обоснования и анализа инвестиционных проектов.
| Вывод: рубль сегодня стоит больше, чем рубль, который мы получим в будущем. Рубль, полученный сегодня, можно немедленно вложить в дело, и он будет приносить прибыль. Или его можно положить на банковский счет и получать процент. |
Наиболее простым и очевидным примером справедливости этой аксиомы является динамика средств, внесенных на сберегательный счет в банке.
Предположим, что мы сегодня можем положить 1000 руб. на депозит под 5 % годовых. Через год сумма на сберегательном счете составит 1050 руб.
В нашем примере будущая стоимость (future value или FV) сегодняшних 1000 руб. при ставке 5 % годовых составит 1050 руб.
 ,
,
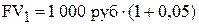 ,
,
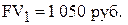
Если мы не будем изымать деньги из банка и оставим их там на второй и третий годы, то окончательная сумма после завершения двухлетнего и трехлетнего периода соответственно составит:
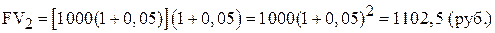 ;
;
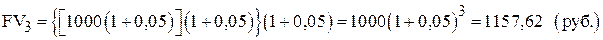
Эта модель умножения сбережений, известная как модель сложных процентов, в общем виде может быть записана следующим образом:
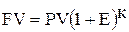 , (5.1)
, (5.1)
где FV – будущая величина той суммы, которую мы инвестируем в любой форме сегодня и которой будем располагать через интересующий нас период времени, в течение которого эти деньги будут работать;
PV (present value) – текущая (современная) величина той суммы, которую мы инвестируем ради получения дохода в будущем;
E – величина доходности инвестиций, в данном примере она равна ставке банковского процента по сберегательному вкладу, а в более общем случае – прибыльности инвестиций;
к – число стандартных периодов времени, в течение которых наши инвестиции будут участвовать в коммерческом обороте.
| Как видно, из указанной формулы для расчета будущей стоимости (FV) мы применяем сложный процент. Это означает, что процент, начисленный на первоначальную сумму, прибавляется к этой первоначальной сумме и на него также начисляется процент. |
Теперь попробуем решить обратную задачу, т.е. определить текущую (современную) стоимость (PV) (или определение того, сколько надо было бы инвестировать сегодня, чтобы получить некоторую сумму в будущем).
Для осуществления такого расчета используется формула, которая является обратной по смыслу формуле (5.1):
PV= 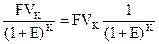 . (5.2)
. (5.2)
Следовательно, текущая (современная) стоимость равна будущей стоимости, умноженной на коэффициент 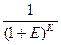 , называемый коэффициентом дисконтирования. , называемый коэффициентом дисконтирования.
|
В нашем примере текущая стоимость (PV) 1000 руб., которые будут получены через 3 года при 5 % годовых, составит
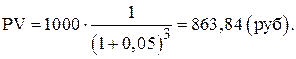
Определяя величину текущей стоимости (PV) исходя из суммы будущей стоимости, мы проводим дисконтирование будущей стоимости.
| Дисконтированием называется процесс приведения (корректировки) будущей стоимости денег к их текущей (современной стоимости). Процесс, обратный дисконтированию, а именно, определение будущей стоимости, есть не что иное, как начисление сложных процентов на первоначально инвестируемую стоимость. |
Процессы начисления сложных процентов и дисконтирования являются столь же древними, как и сам процесс кредитования, и используются финансовыми институтами с незапамятных времен.
Коэффициенты дисконтирования не требуется каждый раз считать отдельно, они приводятся в специальных таблицах (если невозможно применение специального программируемого калькулятора).
5.2.1.3. Будущая стоимость аннуитета [19]
Одним из ключевых понятий в финансовых и коммерческих расчетах является понятие аннуитета. Логика, заложенная в схему аннуитетных платежей, широко используется в анализе инвестиционных проектов, при оценке долговых и долевых ценных бумаг, а также в анализе аренды. Аннуитет представляет собой частный случай денежного потока, а именно: это поток, в котором денежные поступления (или платежи) в каждом периоде одинаковы по величине [15].
Проанализируем тип финансовых операций, предполагающий ежегодный взнос денежных средств ради накопления определенный суммы в будущем.
Пример 5.1. Предположим, что мы будем вносить ежегодно (в конце года) на счет в банке по 1 млн руб. в течение 5 лет при ставке по депозиту 10 % годовых. Спрашивается, какой суммой мы будем располагать спустя 5 лет [19]?
Очевидно, что первый миллион пролежит в банке (зарабатывая проценты) 4 года, второй – 3 года, третий – 2 года, четвертый – один год, а пятый – нисколько. С помощью формулы (5.1) расчета будущей стоимости мы можем найти ту величину, до которой возрастет каждый из взносов до момента изъятия общей суммы со счета. А затем, сложив эти суммы, найдем окончательную величину вклада, которой будем располагать через 5 лет. Запишем это следующим образом.
Таблица 5.1
Расчет будущей стоимости инвестиций
| Номер ежегодного платежа | Время, в течение которого зарабатывается процентный доход (годы) | Будущая стоимость годового вклада, млн руб. |
| 1,0(1+0,1)4 = 1,464 | ||
| 1,0(1+0,1)3 = 1,331 | ||
| 1,0(1+0,1)2 = 1,210 | ||
| 1,0(1+0,1)1 = 1,100 | ||
| 1,0(1+0,1)0 = 1,000 | ||
| Итого будущая стоимость 6,105 |
Если изобразить этот процесс графически, то мы получим схему нарастания будущей суммы аннуитета (рис. 5.1).
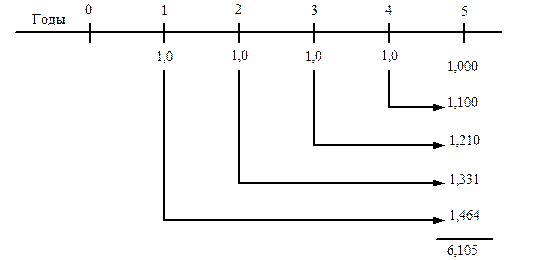
Рис. 5.1. Будущая стоимость аннуитета [19]
Эту схему расчета можно выразить уравнением
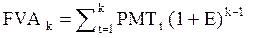 , (5.3)
, (5.3)
где FVAk – будущая стоимость аннуитета (future value of annuity);
PMTt – платеж, осуществленный в конце периода t (payment);
E – уровень дохода;
k – число периодов, в течение которых получается доход.
Если суммы платежей одинаковы в каждом периоде, то это уравнение можно представить в виде
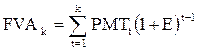 (5.3а)
(5.3а)
или
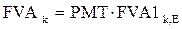 , (5.4)
, (5.4)
где FVA1k,E - будущая стоимость аннуитета в один руб. в конце каждого периода получения доходов на протяжении K периодов и при ставке процентного дохода на уровне E, рассчитываемая по формуле
 .
.
Такой аннуитет обычно называют уровневым, или унифицированным (стандартным), так как платежи одинаковы по всем периодам. И в дальнейшем термин «аннуитет» без дополнительных определений будет означать унифицированный (стандартный) аннуитет.
Нарастание сумм при аннуитете можно рассчитать с помощью калькулятора, электронных таблиц или определить с помощью специальных таблиц (прил. 2). В последнем случае для определения будущей величины аннуитета необходимо будет только по таблице найти будущую стоимость один руб. в году K при ставке процента E, а затем умножить полученный коэффициент на годовую сумму денежного потока (РМТ).
Пример 5.2. Предприятие имеет возможность ежегодно перечислять на накопительный счет в банке под 8 % годовых денежные средства в сумме 12 млн рублей течение 4 лет для реконструкции очистных сооружений. Какой суммой будет располагать предприятие спустя 4 года?
Проведем расчет, используя данные таблиц из прил. 2:
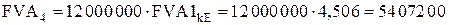 .
.
В инвестиционных проектах встречаются задачи обратного типа.
Например, предприятие запланировало через 3 года приобрести координатно-расточной станок стоимостью 3 000 тыс. руб. Открыт накопительный счет в банке со ставкой 7 % годовых. Следует определить, сколько надо предприятию ежегодно перечислять на этот счет, чтобы к концу третьего года иметь сумму, достаточную для приобретения станка (без учета инфляции).
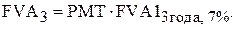
Отыскав в таблице прил. 2 значение для коэффициента для трех лет накопления и ставки в 7 % (он равен 3,215), определяем необходимую величину ежегодных платежей (РМТ):
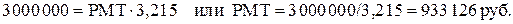
5.2.1.4. Текущая стоимость аннуитета [19]
Основой всех расчетов, проводимых при обосновании и анализе инвестиционных проектов, является сопоставление затрат, которые необходимо осуществить в настоящее время, и тех денежных поступлений, которые можно получить в будущем.
В решении этой проблемы помогает подход, предполагающий определение текущей (современной) стоимости аннуитета. На этой основе достаточно четко можно представить, насколько окупится сегодняшнее вложение средств завтрашними выгодами.
Понять смысл такого анализа будет легче, если мы рассмотрим в качестве примера инвестиционный проект, предполагающий получение 1 млн руб. в конце каждого из пяти последующих лет. Приведенную стоимость (исходя из процентной ставки – нормы дисконта – на уровне 10 % годовых) для каждого из будущих притоков денег мы можем определить с помощью формулы (5.2) и прил. 3. Полученные результаты приведены в табл. 5.2.
Таблица 5.2
Расчет текущей стоимости аннуитета
| Годы | Денежные потоки (денежные поступления), млн руб. | Текущая стоимость будущих денежных поступлений, млн руб. |
1,00 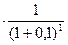 =0,909 =0,909
| ||
1,00 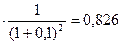
| ||
1,00 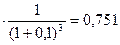
| ||
1,00 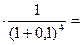 0,683 0,683
| ||
1,00 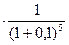 =0,621 =0,621
| ||
| Итого текущая стоимость 3,79 |
Графически этот процесс изображен на рис. 5.2.
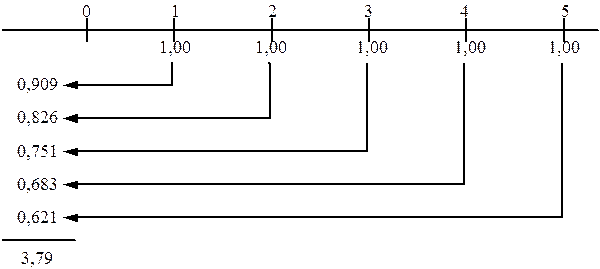
Рис. 5.2. Схема формирования текущей стоимости аннуитета
Логика такого пересчета будет неизменной для любого числа лет жизни объекта, созданного в результате инвестиций. Расчет был проведен по формуле (5.2) следующим образом:
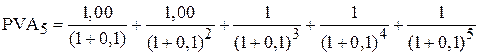 .
.
Отсюда общее уравнение расчета текущей стоимости аннуитета:
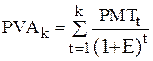 , (5.5)
, (5.5)
где PMTt – будущие поступления денежных средств в конце периода t;
E – норма доходности по инвестициям;
k – число периодов, на протяжении которых в будущем поступят доходы от современных инвестиций.
В случае, если денежные поступления одинаковы в каждом периоде, формулу можно упростить и представить в следующем виде:
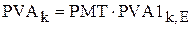 , (5.6)
, (5.6)
где 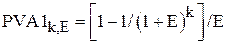 - текущая (современная) стоимость аннуитета стоимостью в 1 руб. в конце каждого из k периодов при ставке доходности на уровне E.
- текущая (современная) стоимость аннуитета стоимостью в 1 руб. в конце каждого из k периодов при ставке доходности на уровне E.
Найти нужное значение с помощью формул (5.5) и (5.6) можно благодаря системам электронных таблиц или справочным таблицам (прил. 4). Если для решения этой задачи мы воспользовались справочной таблицей, содержащей значения аннуитета в один руб., то, по сути дела, нашли коэффициент приведения будущей стоимости к современной (коэффициент дисконтирования), и далее надо просто умножить этот коэффициент на реальные суммы аннуитета.
Пример 5.3. Предположим, что для приобретения нового оборудования необходимы денежные средства в сумме 100 тыс. руб., которые обеспечат ежегодное получение денежных поступлений после уплаты налогов в сумме 25 тыс. руб. в течение шести лет без существенных ежегодных колебаний. Хотя оборудование после шести лет эксплуатации не будет полностью изношено, тем не менее, вряд ли возможно предполагать, что на этот момент времени его стоимость будет превышать стоимость лома. Затраты на ликвидацию будут возмещены за счет выручки от продажи лома. Линейная амортизация за эти шесть лет (16 667 руб. за год) будет соответственно включена в сумму денежных поступлений 25 тыс. руб.
Чтобы оценить этот проект в самом первом приближении, достаточно прикинуть, покроет ли текущая (современная) стоимость будущих денежных поступлений те затраты, которые фирме придется осуществить сейчас. Реально это означает, что нам следует определить чистую текущую стоимость, которую фирма получит от реализации такого проекта.
При проведении расчетов будем исходить из ставки доходности (нормы дисконта) на уровне 10 % годовых.
Результаты расчетов сведены в табл. 5.3.
Таблица 5.3
Расчет текущей стоимости денежных потоков
| Период времени (годы) | Инвестиции (руб.) | Денежные поступления | Текущая стоимость 1 руб. денежных потоков разных лет (коэффициенты дисконтирования при ставке 10%) | Текущая стоимость денежных потоков разных лет, руб. |
| 0 (сегодня) | 100 000 | 1,000 | –100 000 | |
| 25 000 | 0,909 | +22 725 | ||
| 25 000 | 0,826 | +20 650 | ||
| 25 000 | 0,751 | +18 775 | ||
| 25 000 | 0,683 | +17 075 | ||
| 25 000 | 0,621 | +15 525 | ||
| 25 000 | 0,564 | +14 100 | ||
| Чистая текущая стоимость проекта | +8 850 |
Как показали расчеты, для данного проекта чистая текущая стоимость оказалась положительной. Иными словами, осуществление инвестиционного проекта привело к росту капитала фирмы на 8 850 руб. в современном исчислении. Следовательно, инвестиции оказались полезными и привели к росту ценности фирмы.
Дата добавления: 2015-01-21; просмотров: 1232;
