Собственная проводимость полупроводников

Полупроводниками являются твердые тела, которые при T = 0 характеризуются полностью занятой электронами валентной зоной, отделенной от зоны проводимости сравнительно узкой ( 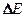порядка 1 эВ) запрещенной зоной (рис. 314, г). Своим названием они обязаны тому, что их электропроводность меньше электропроводности металлов и больше электропроводности диэлектриков.

В природе полупроводники существуют в виде элементов (элементы IV, V и VI групп Периодической системы элементов Менделеева), например Si, Ge, As, Se, Те, и химических соединений, например оксиды, сульфиды, селениды, сплавы элементов различных групп. Различают собственные и примесные полупроводники. Собственными полупроводниками являются химически чистые полупроводники, а их проводимость называется собственной проводимостью. Примером собственных полупроводников могут служить химически чистые Ge, Se, а также многие химические соединения: InSb, GaAs, CdS и др.

При 0 К и отсутствии других внешних факторов собственные полупроводники ведут себя как диэлектрики. При повышении же температуры электроны с верхних уровней валентной зоны I могут быть переброшены на нижние уровни зоны проводимости II (рис.315). При наложении на кристалл электрического поля они перемещаются против поля и создают электрический ток. Таким образом, зона II из-за ее частичного «укомплектования» электронами становится зоной проводимости. Проводимость собственных полупроводников, обусловленная электронами, называется электронной проводимостью или проводимостью п-типа (от лат. negative — отрицательный).

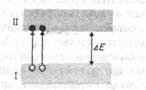
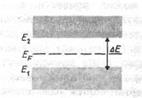
Рис. 315 Рис. 316

В результате тепловых забросов электронов из зоны I в зону II в валентной зоне возникают вакантные состояния, получившие название дырок. Во внешнем электрическом поле на освободившееся от электрона место — дырку — может переместиться электрон с соседнего уровня, а дырка появится в том месте, откуда ушел электрон, и т. д. Такой процесс заполнения дырок электронами равносилен перемещению дырки в направлении, противоположном движению электрона, так, как если бы дырка обладала положительным зарядом, равным по величине заряду электрона. Проводимость собственных полупроводников, обусловленная квазичастицами — дырками, называется дырочной проводимостью или проводимостью р-типа (от лат. positive — положительный).

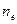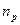Таким образом, в собственных полупроводниках наблюдаются два механизма проводимости: электронный и дырочный. Число электронов в зоне проводимости равно числу дырок в валентной зоне, так как последние соответствуют электронам, возбужденным в зону проводимости. Следовательно, если концентрации электронов проводимости и дырок обозначить соответственно и , то

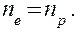(242.1)

Проводимость полупроводников всегда является возбужденной, т. е. появляется только под действием внешних факторов (температуры, облучения, сильных электрических полей и т.д.).

В собственном полупроводнике уровень Ферми находится в середине запрещенной зоны (рис.316). Действительно, для переброса электрона с верхнего уровня валентной зоны на нижний уровень зоны проводимости затрачивается энергия активации, равная ширине запрещенной зоны 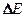. При появлении же электрона в зоне проводимости в валентной зоне обязательно возникает дырка. Следовательно, энергия, затраченная на образование пары носителей тока, должна делиться на две равные части. Так как энергия, соответствующая половине ширины запрещенной зоны, идет на переброс электрона и такая же энергия затрачивается на образование дырки, то начало отсчета для каждого из этих процессов должно находиться в середине запрещенной зоны. Энергия Ферми в собственном полупроводнике представляет собой энергию, от которой происходит возбуждение электронов и дырок.

Вывод о расположении уровня Ферми в середине запрещенной зоны собственного полупроводника может быть подтвержден математическими выкладками. В физике твердого тела доказывается, что концентрация электронов в зоне проводимости

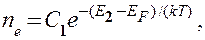(242.2)

где 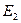— энергия, соответствующая дну зоны проводимости (рис.316), 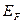— энергия Ферми, Т — термодинамическая температура, 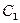— постоянная, зависящая от температуры и эффективной массы электрона проводимости. Эффективная масса — величина, имеющая размерность массы и характеризующая динамические свойства квазичастиц — электронов проводимости и дырок. Введение в зонную теорию эффективной массы электрона проводимости позволяет, с одной стороны, учитывать действие на электроны проводимости не только внешнего поля, но и внутреннего периодического поля кристалла, а с другой стороны, абстрагируясь от взаимодействия электронов проводимости с решеткой, рассматривать их движение во внешнем поле как движение свободных частиц.

Концентрация дырок в валентной зоне

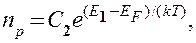(242.3)

где 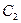— постоянная, зависящая от температуры и эффективной массы дырки, 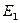— энергия, соответствующая верхней границе валентной зоны. Энергия возбуждения в данном случае отсчитывается вниз от уровня Ферми (рис. 316), поэтому величины в экспоненциальном множителе (242.3) имеют знак, обратный знаку экспоненциального множителя в (242.2). Так как для собственного полупроводника 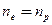(242.1), то

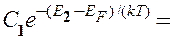
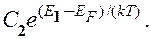
Если эффективные массы электронов и дырок равны ( 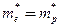), то 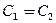и, следовательно,

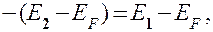
откуда

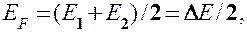
т. е. уровень Ферми в собственном полупроводнике действительно расположен в середине запрещенной зоны.

Так как для собственных полупроводников 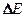>> kT, то распределение Ферми — Дирака (235.2) переходит в распределение Максвелла — Больцмана. Положив в (236.2) 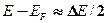, получим

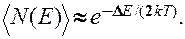(242.4)

Количество электронов, переброшенных в зону проводимости, а следовательно, и количество образовавшихся дырок пропорциональны 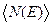. Таким образом, удельная проводимость собственных полупроводников

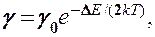(242.5)

где 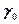— постоянная, характерная для данного полупроводника.

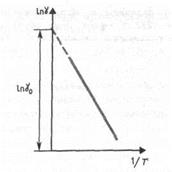
Рис. 317

Увеличение проводимости полупроводников с повышением температуры является их характерной особенностью (у металлов с повышением температуры проводимость уменьшается). С точки зрения зонной теории это обстоятельство объяснить довольно просто: с повышением температуры растет число электронов, которые вследствие теплового возбуждения переходят в зону проводимости и участвуют в проводимости. Поэтому удельная проводимость собственных полупроводников с повышением температуры растет.

Если представить зависимость 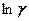от 1/Т то для собственных полупроводников— это прямая (рис.317), по на клону которой можно определить ширину запрещенной зоны 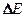, а по ее продолжению — 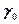(прямая отсекает на оси ординат отрезок, равный ).

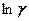Одним из наиболее широко распространенных полупроводниковых элементов является германий, имеющий решетку типа алмаза, в которой каждый атом связан ковалентными связями (см. § 71) с четырьмя ближайшими соседями. Упрощенная плоская схема расположения атомов в кристалле Ge дана на рис. 318, где каждая черточка обозначает связь, осуществляемую одним электроном. В идеальном кристалле при 0 К такая структура представляет собой диэлектрик, так как все валентные электроны участвуют в образовании связей и, следовательно, не участвуют в проводимости.

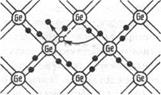
Рис. 318

При повышении температуры (или под действием других внешних факторов) тепловые колебания решетки могут привести к разрыву некоторых валентных связей, в результате чего часть электронов отщепляется и они становятся свободными. В покинутом электроном месте возникает дырка (она изображена белым кружком), заполнить которую могут электроны из соседней пары. В результате дырка, так же как и освободившийся электрон, будет двигаться по кристаллу. Движение электронов проводимости и дырок в отсутствие электрического поля является хаотическим. Если же на кристалл наложить электрическое поле, то электроны начнут двигаться против поля, дырки — по полю, что приведет к возникновению собственной проводимости германия, обусловленной как электронами, так и дырками.

В полупроводниках наряду с процессом генерации электронов и дырок идет процесс рекомбинации: электроны переходят из зоны проводимости в валентную зону, отдавая энергию решетке и испуская кванты электромагнитного излучения. В результате для каждой температуры устанавливается определенная равновесная концентрация электронов и дырок, изменяющаяся с температурой пропорционально выражению (242.4).