ПРИЛОЖЕНИЕ 1. Модульный учебный комплекс МУК-ОК «КВАНТОВАЯ ОПТИКА»

Модульный учебный комплекс МУК-ОК «КВАНТОВАЯ ОПТИКА»

Позволяет проводить лабораторные работы по темам:

4. Внешний фотоэффект;

5. Внутренний фотоэффект;

6. Фотодиод:

· Фотодиодный режим;

· Вентильный фотоэффект;

7. Опыт Франка-Герца;

8. Тепловое излучение;

9. Вакуумный диод:

· Контактная разность потенциалов;

· Распределение электронов по скоростям при термоэлектронной эмиссии.

В состав комплекса входят:

Блок амперметра-вольтметра

Блок управления монохроматическими источниками (8 длин волн) с регулируемой интенсивностью.

Два источника напряжения

Блок питания лампы с регистрацией напряжения и тока.

Регистратор излучения на двух длинах волн(0.6 мкм и 0.95 мкм)

Стенд, содержащий:

· -фотоэлемент

· -фоторезистор

· -фотодиод

· -тиратрон для наблюдения опыта Франка-Герца

· Вакуумный диод

ПРИЛОЖЕНИЕ к лаб. работам № 46^а, 47

В квантовой теории показано [3], что электронный газ, находящийся в равновесном состоянии, подчиняется статистике Ферми-Дирака

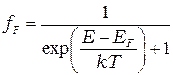, (П-1)

где 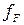- среднее число электронов, находящихся в состоянии с энергией 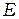при температуре 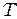и значении уровня энергии Ферми .

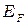Используя законы квантовой механики, можно показать, что плотность квантовых состояний 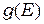при энергии 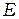, массе частицы 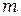и объеме тела 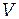определяется выражением

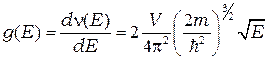, (П-2)

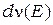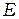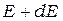где - количество квантовых состояний в узком диапазоне энергий от до . В формуле учтено, что в каждом энергетическом состоянии могут находиться два электрона, обладающих спинами разных знаков.

Число электронов, находящихся в этих состояниях, определяется, следовательно, выражением

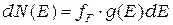, (П-3)

где 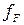и 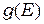даются формулами (П-1) и (П-2) соответственно.

В теории электронной эмиссии, кроме распределения по энергиям (П-3), для вычисления эмиссионного тока важно знать распределение электронов по скоростям. Сделав в (П-3) замены,

, ,

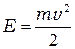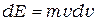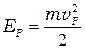
получим

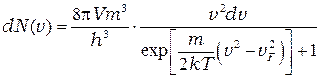. (П-4)

Отсюда, учитывая, что в пространстве скоростей величина 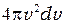равна объему шарового слоя, которому соответствует число электронов 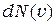, получим число электронов в элементе объема этого пространства :

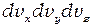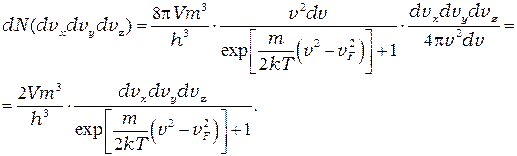
Для того чтобы получить распределение электронов по одной компоненте скорости, проинтегрируем полученное выражение по 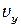и 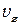в пределах от 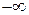до :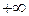

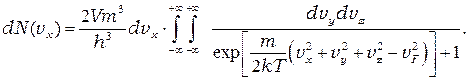
Результат интегрирования имеет вид

.

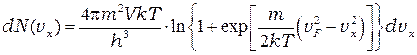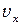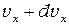Отсюда получим число электронов, попадающих за единицу времени на единичную площадь, скорость которых лежит в диапазоне от до [1]:

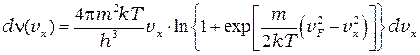. (П-5)

Работа выхода.

Выходу свободных электронов за пределы вещества препятствует электрическое поле, действующее в узкой области вблизи поверхности и создающее потенциальный барьер.

Для металлов возникновение поверхностного потенциального барьера объясняется, во-первых, действием индуцированного положительного заряда поверхности, которую покинул отрицательный электрон (так называемые, силы зеркального изображения), и, во-вторых, действием двойного электрического слоя, существующего на границе металл-вакуум благодаря электронному облаку у поверхности металла.

В диэлектриках возникновение потенциального барьера объясняется поляризацией молекул диэлектрика электрическим полем электрона, вылетающего в вакуум.

У полупроводников, кроме отмеченных выше механизмов, важную роль играют, так называемые, поверхностные состояния. Возможны ситуации, когда поверхность полупроводника будет отдавать электроны в объем вещества и, следовательно, заряжаться положительно, либо, наоборот, захватывать электроны из объема и заряжаться отрицательно. При этом возникает электрический поверхностный потенциал, величина и знак которого могут, в разных ситуациях, как затруднить, так и существенно облегчить выход электрона из полупроводника в вакуум.

Минимальная энергия, которой должен обладать электрон, чтобы, преодолев потенциальный барьер у поверхности вещества, оказаться в вакууме, имея нулевую кинетическую энергию, называется работой выхода электрона из данного вещества.

Плотность термоэлектронного тока.

Если число электронов, выходящих изнутри катода через единичный по площади участок поверхности за единицу времени, равно 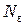, то плотность тока будет равна

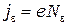, (П-6)

где 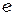- элементарный заряд.

Если 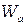- высота потенциального барьера у поверхности катода электронной лампы, то те электроны, для которых выполняется условие

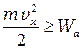, (П-7)

преодолеют потенциальный барьер и окажутся эмитированными. (Считаем, что ось Х направлена перпендикулярно плоской поверхности катода в сторону анода). Значит, к аноду будут двигаться только электроны, скорость которых больше

.

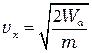Для вычисления 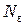воспользуемся формулой (5), которую необходимо проинтегрировать с учетом условия (7)

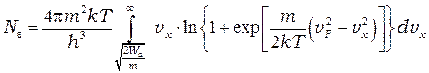
Поскольку величина

,

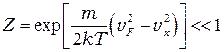можно воспользоваться разложением логарифма в ряд

,

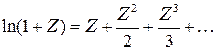ограничившись первым членом:

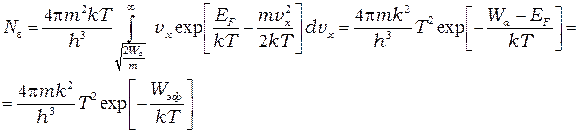(П-8)

Величина 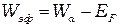называется эффективной работой выхода.

Используя для величины 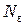выражение (П-8), получим следующее выражение для плотности термоэлектронного тока:

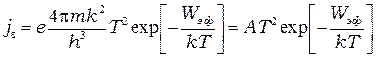, (П-9)

где .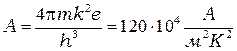

Выражение (П-9) называется формулой Ричардсона-Дешмана.

Согласно законам квантовой механики, электрон, пролетающий область потенциального барьера, имеет отличную от нуля вероятность отразиться от барьера, даже если для него выполняется условие (П-7). Как показывает расчет, для реально существующего потенциального барьера, имеющего форму монотонно возрастающей функции от координаты Х, коэффициент прозрачности барьера 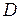близок к единице: 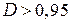для металла. Следовательно, строго говоря, плотность термоэлектронного тока с учетом квантового эффекта отражения следует записывать в виде формулы

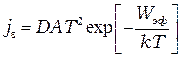, (П-10)

где 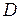- коэффициент прозрачности барьера.

Распределение эмитированных электронов.

Электроны в катоде, способные к эмиссии, принадлежат к числу наиболее быстрых. Для быстрых электронов распределение в квантовой статистике при температуре 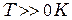совпадает с классическим распределением Максвелла. Важно выяснить, сохраняется ли это распределение после того, как электроны преодолели потенциальный барьер.

Обозначим скорость электронов в направлении оси Х после преодоления барьера 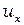. Тогда

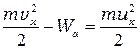, (П-11)

где 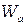- высота потенциального барьера.

Из (П-11) следует

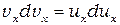. (П-12)

Тогда, переходя в формуле (П-5) к переменной 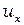, применяя разложение логарифма в ряд, как это делалось при выводе формулы (П-8), используя (П-11), (П-12), а, также учитывая отражение от барьера, получим формулу для числа электронов, прошедших потенциальный барьер, и имеющих после этого скорость в диапазоне от 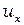до

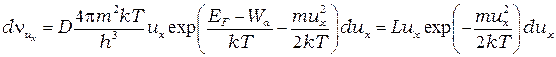, (П-13)

где .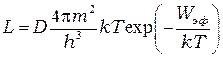

Если коэффициент прозрачности потенциального барьера 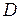не зависит от скорости электронов, то формула (П-13) показывает, что распределение электронов остается максвелловским и после прохождения ими барьера. Для большинства катодов, особенно металлических ( 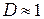), это выполняется.

Учитывая формулу (П-8) для коэффициента 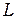можно записать

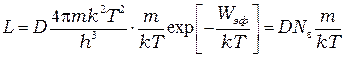. (П-14)

ЛИТЕРАТУРА

1. Савельев И. В. Курс общей физики, т. 2. Электричество и магнетизм.

Волны. Оптика: Учебное пособие. - 2-е изд., перераб. - М.: Наука. Главная редакция физико-математической литературы, 1982. - 496 с.

2. Трофимова Т. Н. Курс физики: Учеб. пособие для вузов. -6-е изд., стер - М.: Высш. шк., 1999. - 542 с: ил. ISBN 5-06-003634-0

3. Детлаф А.А., Яворский Б. М. Курс физики. - М.: Высш. шк., 1988, с. 387-399.

4. Баранов А. В.и др. Колебания и волны. Оптика. Квантовая механика. Кн. 2. – Новосибирск: Изд-во НГТУ, 1994.

5. Ландсберг Г.С. Оптика. – М.: Наука, 1976. – 926 с.

6. Иродов И. Е. Волновые процессы. Основные законы. т.4. – М.: Лаборатория базовых знаний, 1999, – 256 с.

7. Кингсеп А. С., Локшин Г. Р., Ольхов О. А. Основы физики. Курс общей физики: Учебн. В 2 т. Т. 1. Механика, электричество и магнетизм, колебания и волны, волновая оптика / Под ред. А.С. Кингсепа. — М.: ФИЗМАТЛИТ, 2001, - 560 с. — ISBN 5-9221-0164-1 (Т. 1).

8. Белонучкин В. Е., Заикин Д. А., Ципенюк Ю.М., Основы физики. Курс общей физики: Учебн. В 2 т. Т. 2. Квантовая и статистическая физика / Под ред. Ю.М. Ципенюка. - М.: ФИЗМАТЛИТ, 2001. - 504 с. - ISBN 5-9221-0165-Х (Т. 2).

9. Стафеев С. К., Боярский К. К., Башнина Г. Л. С78 Основы оптики: Учебное пособие. - СПб.: Питер, 2006, - 336 с: ил. ISBN 5-469-00846-0.10. Р.

10. Дитчберн. Физическая оптика. – М.: Наука, 1965,- 632 с.

11. Годжаев Н.М. Оптика. – М.: Наука: Высшая школа, 1977, - 422 с.

13. Руководство к лабораторным занятиям по физике. Под ред. Л.Л. Гольдина. М: Наука, 1973.

14. Борн М., Вольф Э. Основы оптики. М., Наука.1970, - 855 с.

15. Дмитриева В.Ф. Основы физики: Учеб. пособие для студентов вузов. - 2-е изд. - М.: Высш. шк., 2001. - 527c.:ил.

16. Лебедева В.В. Техника оптической спектроскопии. М.: Изд-во Моск. Ун-та, 1977.

17. В.И.Гапонов Электроника, Ч.1, М.: 1960.

18. Епифанов Г.И. Физика твердого тела – М.: Высшая школа, 1965.

Позиция № 251

в плане издания

учебной литературы

МГУ на 2010 г.

Учебное издание

Юрий Дмитриевич Воробьёв

Волновая оптика Дифракция

Учебное пособие

Печатается в авторской редакции

6,3 уч.-изд. л. Формат 60 ´ 84 1/16

Тираж 100 экз. Заказ №

Отпечатано в типографии РПК МГУ им. адм. Г. И. Невельского

690059, Владивосток, ул. Верхнепортовая, 50а