Равновесные носители тока в полупроводнике

Ширина запрещённой зоны 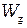, у типичных полупроводников лежит в пределах от нескольких десятых электрон-вольта до двух-трех электрон-вольт (табл.1). Напомним, что единица энергии 1 эВ = 1,6 10^-19 Дж.

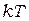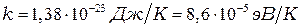Разрыв электронных связей и образование электронов проводимости в полупроводнике может происходить за счет тепловых колебаний атомов кристаллической решетки. Средняя энергия теплового движения частиц по порядку величины равняется, как известно, , где - постоянная Больцмана.

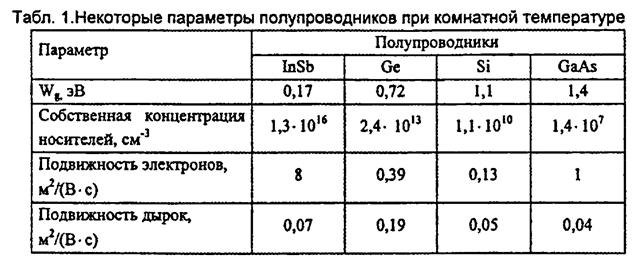
При комнатной температуре 300К энергия теплового движения 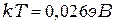, т.е. значительно меньше ширины запрещённой зоны 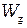. Несмотря на это, тепловое движение вызывает разрывы электронных связей, так как мгновенная кинетическая энергия атома может во много раз превышать её среднее значение.

Согласно статистическому распределению Больцмана, вероятность 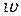обнаружить атом в состояния с энергией, равной или большей 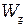, пропорциональна:

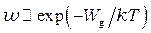. (9)

Для описания электронной и дырочной компонент тока применимы соотношения (1 - 4), в формулах (1) и (2) знак «минус» соответствует электронам, а знак «плюс» - дыркам. Полная плотность тока, очевидно, равна

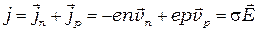
где 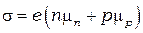индекс «n» относится к электронам, «p» - к дыркам.

Таким образом, тепловое движение непрерывно создает (генерирует) электроны проводимости и дырки. В то же время идут и обратные процессы рекомбинации, в результате которых свободные электроны вновь захватываются атомами, что приводит к одновременному исчезновению электрона и дырки. В установившемся состоянии существует динамическое равновесие процессов генерации и рекомбинации. В результате при данной температуре устанавливается равновесная концентрация электронов и дырок.

Число электронно-дырочных пар 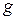, создаваемых каждую секунду в единице объема полупроводника, т.е. скорость генерации, в соответствии с (9) равна

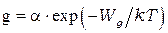, (10)

где 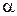- коэффициент пропорциональности, различный для разных полупроводников.

Вероятность одновременного появления в произвольной точке кристалла электрона и дырки, т.е. их встречи и рекомбинации, должна быть пропорциональной произведению концентраций электронов и дырок. Таким образом, число пар, рекомбинирующих каждую секунду в единице объема, т.е. скорость рекомбинации 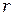, равна

.

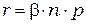Коэффициент пропорциональности‚ 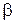, как и 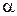в формуле (10), различен для разных полупроводников.

В собственных полупроводниках (без примесей) носители генерируются и рекомбинируют всегда парами. Поэтому 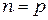. Отсюда следует, что

.

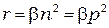В состоянии динамического равновесия 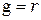. Приравнивая (10) и (12), получим:

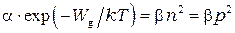
и равновесная концентрация носителей оказывается равной

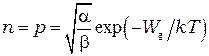(13)

Константа перед экспонентой в (13), очевидно, имеет ту же размерность, что 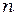и или 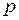. Обозначая её через 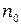или 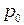, запишем окончательный вид зависимости равновесной концентрации электронов проводимости полупроводника от температуры:

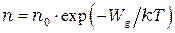(14)

Такую же формулу можно написать и для равновесной концентрации дырок:

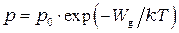(15)

В табл. 1 приведены экспериментальные данные по равновесной концентрации носителей в типичных полупроводниках при комнатной температуре.