Истинное значение измеряемой величины

Приведенные выше данные показывают, что, строго говоря, измерения истинного значения любой величины невозможно в принципе. Поэтому более корректный способ представления результата любого измерения состоит в том, что экспериментатор указывает свою наилучшую оценку измеряемой величины, а также интервал, в котором, как он уверен, она лежит. Таким образом, задача экспериментатора состоит в том, чтобы уменьшить влияние погрешностей за счет правильной техники измерений, сделать правильную наилучшую оценку результата измерения и величины погрешности этого результата.

Рассмотрим случай, когда систематические ошибки отсутствуют, а имеют место лишь случайные погрешности. Предположим, что нами произведено n измерений некоторой величины х, при этом получены n значений этой величины х₁ х₂ х_i….х_n. Округлим эти величины с учетом приборной ошибки и расположим в порядке возрастания. Определим в полученном множестве значений количество повторов (выпадений) отдельных результатов - ∆n_i и вычислим вероятности их выпадения по формуле:

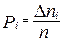(2)

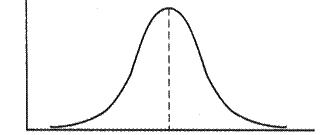
Полученные результаты также внесем в таблицу и построим на их основе график (рис.1) зависимости вероятности повторов отдельных результатов измерения от их величины - х_i, т.е. функцию .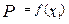

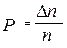P_max

х_i

х_в .

Рис. 1.

Из полученного рис.1 видно, что наиболее вероятным является некоторый результат х_i= х_в, которому соответствует максимальное значение вероятности выпадения P_max.

Если этот результат (х_в) принять за истинный (Хв = Хи), то абсолютную ошибку каждого измерения ∆х_i, можно найти из выражения: ∆х_i= х_i,- х_в и более того истинный результат измерения, очевидно, должен удовлетворять условию:

∆х_i= х_i,- х_в=0 (3)

В этом можно убедиться, рассчитав абсолютные ошибки всех измерений, числа повторов каждой ошибки ∆n₀ и вероятности выпадения ошибок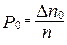

Кроме того, как следует из работ немецкого математика Г. Гаусса, все обсуждаемые выше закономерности наблюдаются на рис 2.

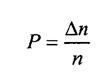
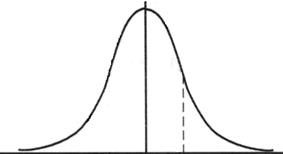
-∆x 0 +∆x_i

Рис. 2.

Для повышения точности и снижения трудоемкости Гаусс предложил для нахождения истинного значения измеряемой величины использовать квадратичную функциональную зависимость вероятности ошибок в виде (4) изображенную на рис.3.

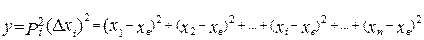(4)

y

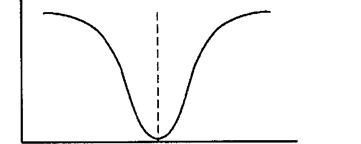
0 (∆х_j)²

Рис.3.

Известно, что для нахождения экстремума функции необходимо приравнять нулю ее производную. Используем для этого новую функцию (4):

Возьмем производную от этой функции и приравняем её нулю.

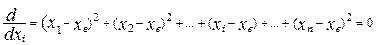(5)

После несложных преобразований получаем:

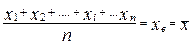(6)

Таким образом, наиболее вероятным значением измеряемой величины является среднее арифметическое 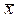, получаемое от нескольких идентичных измерений. И этот же результат соответствует истинному значению многих измерений, представленных на Рис. 1.