Динамические характеристики ВЧ генератора и максимально отдаваемая им мощность

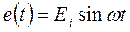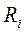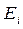Любой генератор отдает максимальную мощность в нагрузку при выполнении определенного условия. Из курса электротехники известно, что генератор с ЭДС и внутренним сопротивлением ; при и 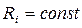отдает в нагрузку максимальную мощность, равную 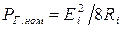, при 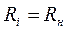(рис. 4.3). Мощность 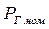называется номинальной мощностью генератора.

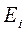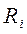В ВЧ генераторах оба параметра ( и ), зависящие от многих факторов, не являются постоянными величинами, и поэтому здесь условие получения максимальной мощности, передаваемой генератором в нагрузку, усложняется и вытекает из понятия «динамическая характеристика генератора по 1-й гармонике сигнала». Пусть в результате эксперимента или расчета найдены зависимости для функций напряжения 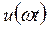и тока 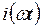, на выходе электронного прибора. Пример графиков таких функций приведен на рис. 4.4,а,б.

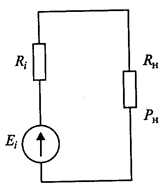
Рис. 4.3. Определение номинальной мощности генератора.

Из двух данных зависимостей, исключив время t, можно получить третью 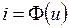, называемую динамической характеристикой ВЧ генератора для мгновенных значений тока и напряжения (рис. 4.4,в).

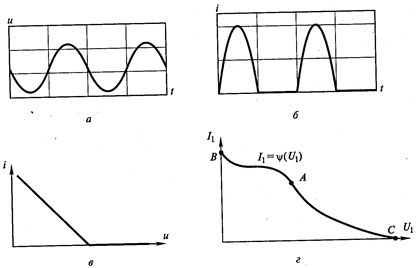Рис. 4.4. Динамическая характеристика ВЧ генератора для

мгновенных значений тока и напряжения

Разложив в ряд Фурье семейство функци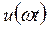й и 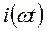, определим первые гармоники тока 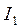и напряжения 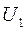. Зависимость 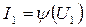называется динамической характеристикой по 1-й гармонике сигнала. Пример такой характеристики приведен на рис. 4.5,г. С ее помощью определим условия передачи максимальной мощности от генератора в нагрузку. Функция 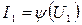является нелинейной, зависящей от частоты и мощности входного сигнала и напряжения питания. Зафиксируем данные параметры и запишем для мощности, передаваемой генератором в нагрузку:

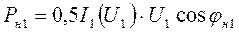, (4.4)

где 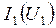- динамическая характеристика ВЧ генератора по 1-й гармонике сигнала (см. рис. 4.5, г); 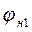- фазовый угол между векторам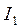и и .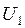

Найдем частную производную функции (4.4) и приравняем ее к нулю для определения экстремума функции:

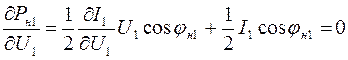, (4.5)

Из (4.5) при 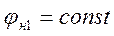получим

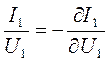. (4.6)

На графике функции 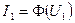(см. рис. 4.5,г ) условию (4.6) передачи максимальной мощности от генератора в нагрузку соответствует точка А, режиму короткого замыкания - точка В, холостого хода - точка С. Раскроем физическое содержание выражения (4.6). Под отношением

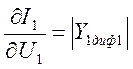
следует понимать модуль внутренней дифференциальной проводимости по 1-й гармонике сигнала эквивалентного генератора. Ее равенство проводимости нагрузки и есть условие передачи максимальной мощности (4.6), которое можно представить в виде

,

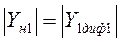где 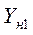- проводимость нагрузки, подключенной к выходу электронного прибора, на частоте 1-й гармоники сигнала.

Точку А на динамической характеристике (см. рис. 4.4,г) можно найти графическим путем как точку пересечения двух графиков согласно (4.6). Для этого необходимо в n-точках динамической характеристики определить значения ее координат 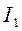и 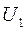и производную 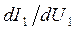как тангенс угла касательной в этой точке. Далее согласно (4.6) построим два графика:

.

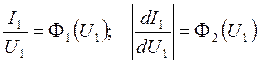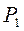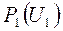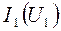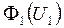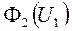Точка пересечения данных графиков определяет условия получения максимальной мощности отдаваемой ВЧ генератором в нагрузку. Чтобы убедиться в этом, следует построить график зависимости . Пример таких построений приведен на рис. 4.5. На рисунке показаны зависимости (см. рис. 4.5,а), и (см. рис. 4.5,б), 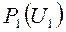(см. рис. 4.5,в).

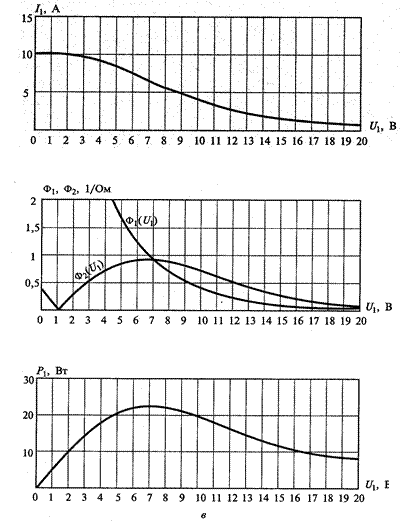Рис. 4.5. Условие получения максимальной мощности, отдаваемой генератором по 1-й гармонике сигнала.