Булевы функции
Для описания функционирования логических схем используются булевы функции.
Булевой функцией n переменных x1, x2, …, xn называется функция вида f = j (x1, x2, …, xn), где переменные xi равны 0 или 1; и функция f равна 0 или 1; переменные объединены конечным числом булевых операций – отрицание, конъюнкция и дизъюнкция.
Область определения булевой функции n переменных – совокупность всевозможных n - мерных наборов, компонентами которых являются двоичные значения 0 и 1. Каждая компонента набора соответствует одной из переменных набора x1, x2, …, xn. Функция n переменных определяется на N = 2n наборах.
Булева функция может задаваться таблицей истинности. В таблице перечисляются всевозможные наборы, составляющие область определения функции, и для каждого набора указывается значение 0, 1 или d, которое имеет функция на этом наборе. Знак d отмечает неопределенное значение функции. На месте неопределенного значения d при необходимости можно указывать значение 0 или 1.
Несущественный набор – набор, на котором функция принимает неопределенное значение. Несущественные наборы появляются в том случае, если значение функции на наборе безразлично или если реально существующая область определения функции состоит из числа наборов, меньшего 2n.
Полностью определенная функция – булева функция, определенная на всем множестве наборов.
Частично определенная функция – булева функция, содержащая несущественные наборы.
Старшинство булевых операций: отрицание, конъюнкция, дизъюнкция. Для изменения порядка выполнения действий используются скобки.
В табл. 1.1 представлены основные логические функции, математическое описание и реализация этих функций с помощью релейно-контактных и логических элементов.
Таблица 1.1. Основные логические функции
| Логическая функция | Математическое описание | Контактная схема | Изображение элемента |
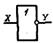
| НЕ (инвертор) | 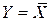
| 
| 
|
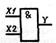
| И (конъюнктор) | Y = X1X2 | 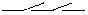
| 
|
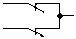
| И – НЕ (штрих Шеффера) | 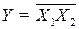
| 
| 
|
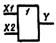
| ИЛИ (дизъюнктор) | Y = X1+X2 | 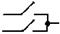
| 
|
| ИЛИ – НЕ (стрелка Пирса) | 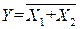
| 
| 
|
Описание логических функций в виде таблиц истинности приведено в табл. 1.2
Таблица 1.2. Таблицы истинности
| НЕ | И; И – НЕ | ИЛИ; ИЛИ – НЕ | |||||||
| X | Y | X2 | X1 | Y | 
| X2 | X1 | Y | 
|
Дата добавления: 2015-01-15; просмотров: 1338;
