Синтез систем дискретной автоматики

Системы электроавтоматики с релейными элементами широко используются для автоматизации различных периодических технологических процессов.

Для управления периодическими процессами и машинами, работающими по циклическому графику, применяются однотактные и многотактные системы автоматического управления.

В однотактных системах, реализующих комбинационные логические функции (ЛФ), наличие сигнала на выходе системы определяется только комбинацией значений сигналов на входе, поступающих от датчиков, задающих и командных устройств, т.е. сигналы на выходе системы однозначно определяются сигналами на входе.

В многотактных системах, реализующих последовательностные ЛФ, сигналы на выходе автоматического устройства определяются не только входными сигналами, поступившими в данный момент, но и последовательностями появления входных сигналов, т.е. при одной и той же комбинации входных сигналов на выходе многотактного автоматического устройства могут быть разные выходные сигналы. Поэтому многотактные устройства и системы должны «запоминать» последовательность появления входных сигналов. Многотактные системы, содержащие элементы «памяти», обратные связи, являются основными системами дискретной автоматики.

Основной задачей синтеза автоматических систем управления является разработка структуры автоматического устройства и составление схем, реализующих полученную структуру.

При этом на основании заданных условий работы автоматического устройства составляются структурные формулы (алгебраические выражения), описывающие работу разрабатываемого автоматического устройства. Затем в результате минимизации получают наиболее простые алгебраические выражения, на основании которых выполняют структурные и электрические схемы. На практике применяют специальные методы логического синтеза структур автоматических систем управления. Достаточно хорошо разработаны методы синтеза, основанные на использовании таблиц состояний и включений, циклограмм, таблиц переходов и карт Карно, с использованием графов.

Синтез дискретных схем по таблицам состояний.

По таким таблицам достаточно просто может быть выполнен синтез однотактных систем управления. Таблицы состояний составляют на основе изучения условий работы технологических аппаратов и определения, при каких соотношениях входных сигналов должны быть сигналы на выходе, а при каких нет. На основании таблиц составляют структурную формулу, описывающую логические связи данной системы и, следовательно, определяющую ее структуру. При составлении структурных формул применяют правило истинности (правило единиц) или же правило ложности (правило нулей).

Согласно правилу единиц для строк таблиц состояний, где выходная величина принимает значение 1, определяют произведения входных величин и складывают их, т.е. определяют дизъюнкции конъюнкций входных переменных для строк, где выходная величина принимает значение 1.

Согласно правилу ложности, структурную формулу составляют путем определения конъюнкции дизъюнкций входных сигналов строк таблиц состояний, в которых выходная величина равна 0.

Пример. Пусть работа объекта контролируется тремя датчиками. Условия работы системы: на выходе логического устройства должен появиться сигнал, приводящий в действие исполнительный элемент X, если на вход поступают два из трех любых сигналов или все три сигнала (мажоритарная функция, схема голосования два из трех).

Таблица состояний (табл. 1.3) для данного примера имеет следующий вид:

Таблица 1.3. Состояние автомата

Структурная формула,, определяющая .условия работы схемы и составленная согласно правилу единиц, имеет вид

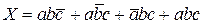. (1.1)

Полученное выражение минимизируется с целью получения структуры. Для этого используются основные законы алгебры логики или специальные методы. Предварительно для упрощения дважды повторим последний член выражения (1.1), а затем сгруппируем и вынесем общие множители, получим

.

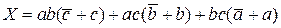Так как выражения в скобках дают 1, то структурная формула имеет вид

Х =ab + ас + bс . (1.2)

Релейно-контакторная схема, реализующая полученную ЛФ, приведена на рис. 1.5. Схема на логических элементах приведена на рис. 1.6.

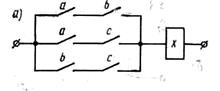
Рис. 1.5. Схемная реализация логических функции (1.2)

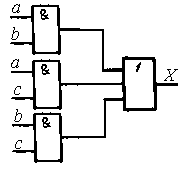
Рис. 1.6. Реализация функции (1.2) на логических элементах

Дальнейшее упрощение (1.2) приводит к виду

X=a (b+c) + b×c . (1.3)

Релейно-контакторная схема, реализующая полученную ЛФ, приведена на рис. 1.7. Схема на логических элементах приведена на рис. 1.8.

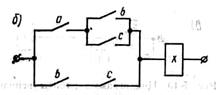
Рис. 1.7. Схемная реализация логических функций (1.3)

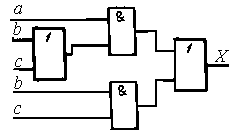
Рис. 1.8. Реализация функции (1.3) на логических элементах