Лекция №34. Определение четырехполюсника. Основне формы записи уравнений четырехполюсника.

Цель: выдать студентам знания по теории четырехполюсников.

Задача: Научить различать различные формы записи уравнений четырехполюсников.

Четырехполюсником называют электрическую цепь (рис.4.1), в которой важными являются две ветви, одна из которых входная, а другая – выходная

Будем считать определяющими величинами: U₁ ,I₁ ,U₂ , I_{2 .}

Поставим цель, считая известными любые две из перечисленных величин, найти две оставшиеся.

Таких вариантов будет шесть. Они определяют следующие формы записи уравнений четырехполюсников:

1) форма Y ;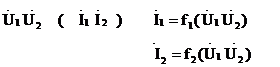

2) форма Z ;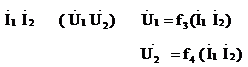

3) форма B ;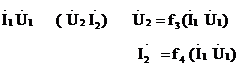

4) форма А ;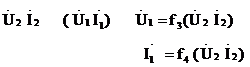

5) форма Н ;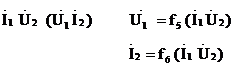

6) форма F .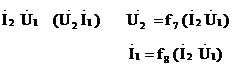

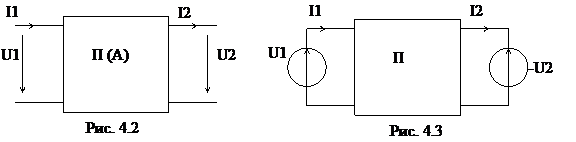
Осуществим вывод уравнений пассивного четырехполюсника в Y-форме. Воспользуемся

методом наложения. Рассмотрим четырехполюсник (рис. 4.2), и проделаем вывод уравнений пассивного четырехполюсника. Для этого четырехполюсник представим в виде рис. 4.3, где входное и выходное напряжения заменены фиктивными источниками.

По принципу независимости действия источников ток в каждой ветви можно определить, суммируя составляющие токов от каждого источника цепи. Схема (рис. 4.3) будет эквивалентна совокупности двух схем (рис. 4.4 и.4.5).

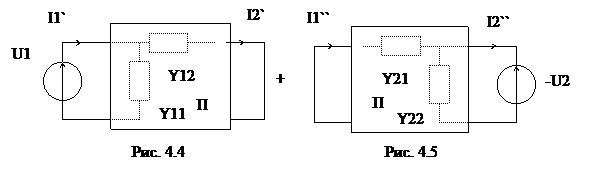
Определим токи 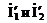по закону Ома:

,

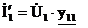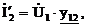
где 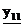– входная проводимость; 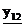– входная проводимость между входом и выходом.

По аналогии:

;

,

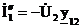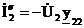где 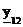выходная проводимость; .

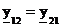В соответствии с методом наложения имеем:

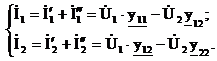
Последние уравнения представляют собой Y-форму записи уравнений четырехполюсника.

Выведем уравнения пассивного четырехполюсника в Z-форме.

Для вывода воспользуемся уравнениями Y-формы:

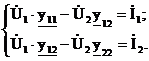
Введем матрицу: 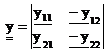, вычислим определители:

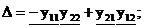
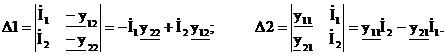
Тогда входное и выходное напряжения равны:

или после формирования столбцов токов:

;

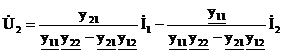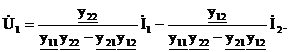
Если ввести матрицы-столбцы напряжений и токов, то можно получить уравнения в матричном виде.

Введем

матрицы-столбцы 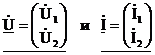, тогда уравнения в матричном виде примут вид в Y-форме:

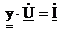
и в Z-форме:

.

Если обозначить коэффициенты в правых частях последних уравнений сопротивлениями, то уравнения Z- формы примут вид:

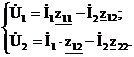
Из этой системы выразим :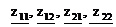

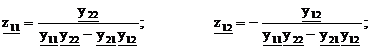
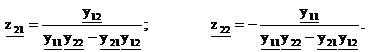
Откуда видно, что .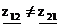

Выведем уравнения пассивного четырехполюсника в А-форме. При выводе также воспользуемся уравнениями Y-формы:

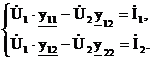
Из первого уравнения получим:

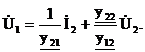
Это напряжение подставим во второе уравнение и найдем ток:

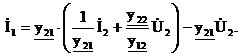
Система уравнений примет вид А-формы:

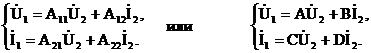
Если в уравнениях поменять местами индексы и коэффициенты А и D, то можно получить уравнения В-формы:

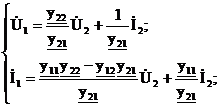
или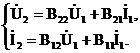

Особое свойство коэффициентов в уравнениях А-формы (проверка расчетов) заключается в том, что разность произведений коэффициентов A, D и B, C равно единице:

AD – BC = 1.

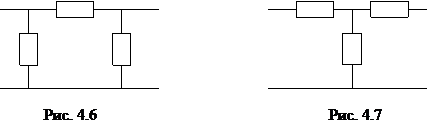
Отсюда следует: любой пассивный четырехполюсник можно представить трехэлементной схемой (рис. 4.6, 4.7).

Поступая аналогично, можно получить уравнения Z-, H-, F-форм.

Вопросы:

· Для решения каких задач применяется теория четырехполюсников?

· Сколько коэффициентов четырехполюсника являются независимыми?

· Какой четырехполюсник называется симметричным?