Схема электрической цепи

Графическое изображение реальной электрической цепи с помощью условных символов и знаков называется электрической схемой.

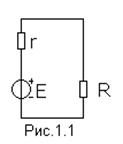Такая схема представляет собой идеализированную цепь, которая служит расчетной моделью реальной цепи и иногда называется эквивалентной схемой замещения. Эта схема по возможности должна отражать реальные процессы, происходящие в действительности.

При проведении расчетов каждый реальный элемент цепи заменяется элементами схемы.

В цепях постоянного тока чаще всего используют два основных элемента: источник энергии с Э.Д.С. Е c внутренним сопротивлением r₀ и резистивный элемент (нагрузка) с сопротивлением R. Под внутренним сопротивлением генератора r₀ понимают сопротивление электрическому току всех элементов внутри генератора.

Сопротивление приёмника R характеризует потребление электрической энергии, то есть превращение электрической энергии в другие виды с выделением мощности:

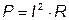. (1.5)

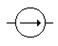Источник Э.Д.С. изображают в виде окружности диаметром 10мм со стрелкой внутри, которая указывает положительное направление Э.Д.С. (или направление увеличения потенциала).

Резистивный элемент принято изображать в виде прямоугольника размером 10 x 4 мм.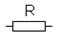

Для проведения анализа электрической цепи важно выделить такие понятия, как ветвь, узел и контур.

Ветвь – участок электрической цепи, образованный последовательно соединёнными элементами и характеризующийся собственным значением тока в данный момент времени.

Узел – это точка соединения трёх и более ветвей (если на электрической схеме в месте пересечения двух линий стоит точка, то в этом месте есть электрическое соединение 2х линий, в противном случае его нет).

Контур – замкнутая часть цепи, состоящая из нескольких ветвей и узлов. Различают такие понятия, как геометрический и потенциальный узел.

На рис. 1.2 приведена схема электрической цепи, содержащей 4 геометрических узла, 3 потенциальных узла и 5 ветвей.

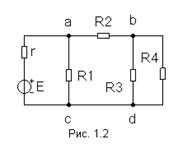Заземление любой точки схемы означает, что потенциал этой точки принят равным нулю.

При проведении расчетов электрических цепей в электротехнике пользуются некоторыми упрощенными моделями:

1. Резистор рассматривается как линейный элемент с сопротивлением R величина которого остаётся постоянной. Однако в действительности при прохождении тока через резистор происходит выделение тепла, что приводит к нагреванию самого резистора и, следовательно, к изменению его сопротивления. Это изменение описывается следующим соотношением:

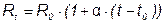, (1.6)

где α – температурный коэффициент сопротивления, 1/град;

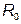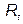и - сопротивление резистора при начальной и конечной температуре соответственно, Ом;

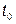- начальная температура, ;

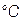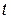– конечная температура, .

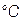Для приближенных расчетов температурный коэффициент сопротивления чистых металлов можно считать равным 0,004 град^-1.

2. Сопротивлением соединительных проводов часто пренебрегают (если их длина невелика < 10 м), а если учитывают, то считают сосредоточенным в одном месте. При этом необходимо учитывать сечение S мм², длину l и материал провода:

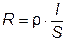, (1.7)

где R – сопротивление проводника, Ом;

ρ – удельное сопротивление проводника, Ом мм²/м;

l - длина проводника, м;

S – поперечное сечение проводника, мм².

Сечение проводника стандартизовано и выбирается из следующего ряда: 0,5; 1,5; 2,5; 4; 6; 10;16; 25; 25; 35; 50; 75; 90; 120мм². При выборе сечения проводов необходимо учитывать, чтобы падение напряжения в линии ∆U при заданной протяженности не превышало допустимого значения 5-10% от номинального.

При рассмотрении электрических цепей совокупность сопротивлений резисторов, соединённых произвольным образом, целесообразно представить в виде одного резистора, обладающего эквивалентным сопротивлением Rэ.

Такой элемент, заменяющий часть цепи и имеющий два входных зажима называется пассивным двухполюсником.

Если выделенная часть цепи содержит источник Э.Д.С. или тока, то соответствующий эквивалентный элемент будет называться активным двухполюсником.

На схемах необходимо указывать положительное направление Э.Д.С. и токов. Это нужно для того, чтобы при проведении расчетов по тем или иным методам было возможным составить необходимые уравнения.