Основы оптимального распределения активной мощности в ЭЭС

Суммарная мощность генераторов ЭЭС, как правило, превышает суммарную потребляемую мощность. Поэтому в рабочий режим включаются не все агрегаты, а какая-то их большая часть. Одним из основных требований, предъявляемых к ЭЭС, является экономичность ее режима работы, отвечающего минимальным затратам на единицу выработанной электроэнергии.

В связи с этим возникает оптимизационная задача экономичного распределения активной мощности между отдельными агрегатами электростанции и между электростанциями в ЭЭС. В качестве критерия оптимальности принимается минимум суммарного расхода топлива В_S при выполнении баланса мощности (2.1).

Рассмотрим сначала задачу оптимального распределения активной мощности между агрегатами одной тепловой станции, работающей на выделенную нагрузку SР_п. Для каждого отдельного агрегата существует так называемая расходная характеристика В(P_г), определяющая зависимость расхода топлива В от мощности, выдаваемой генератором Р_г. Будем считать, что функция В(P_г) дифференцируема.

Для электростанции с n агрегатами целевая функция, подлежащая минимизации, будет иметь вид

В_S = 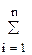B_i(P_гi) ® min. (2.9)

Минимум функции (2.9) ищется при условии выполнения баланса активной мощности для станции. Это условие запишем в виде

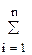Р_гi – åР_п=0. (2.10)

Для целевой функции (2.9) и баланса активной мощности (2.10) запишем функцию Лагранжа и вместо условного минимума целевой функции будем искать безусловный минимум функции Лагранжа

L = 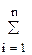B_i(P_гi)+l ( 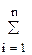P_гi – S P_п) ® min, (2.11)

где l – неопределенный множитель Лагранжа.

Минимум функции Лагранжа достигается при равенстве нулю ее частных производных по всем переменным, т.е. при условиях

¶L/¶P_г1=¶B₁/¶P_г1+l =0;

. . . . . . . . . . . . .

¶L/¶P_гi=¶B_i/¶P_гi +l =0; (2.12)

. . . . . . . . . . . . .

¶L/¶P_гn=¶B_n/¶P_гn+l =0;

¶L/¶l =( 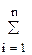P_гi–S P_п) =0.

Из уравнений (2.12) видно, что искомому решению соответствует условие равенства между собой частных производных

¶B₁/¶P_г1=...=¶B_i/¶P_гi=...=¶B_n/¶P_гn=–l =const. (2.13)

Эти частные производные называются относительными приростами расхода топлива и обозначаются e_i (i=1, 2, ... n). Таким образом, оптимальное распределение активной мощности между агрегатами одной станции будет при равенстве относительных приростов расхода топлива отдельных агрегатов станции.

Обычно при решении задачи оптимального распределения активных мощностей используются характеристики относительных приростов e_i(Р_гi), получаемые дифференцированием расходных характеристик B_i(P_гi).

Принцип равенства относительных приростов расхода топлива при оптимизации распределения активной мощности между двумя агрегатами станции иллюстрируется рис. 2.3. При распределении мощности SP_п1 между двумя агрегатами первый агрегат нужно загрузить мощностью Р_г11, а второй – мощностью Р_г21. При этом SP_п1=Р_г11+Р_г21, а относительные приросты расхода топлива e₁ =e₂=e'. При распределении мощности S P_п2 между двумя агрегатами первый агрегат нужно загрузить мощностью Р_г12, а второй – мощностью Р_г22. При этом S P_п2=Р_г12+ Р_г22, а относительные приросты расхода топлива e₁ =e₂=e".

Видно, что до точки пересечения характеристик большую нагрузку следует давать на первый агрегат, а после точки пересечения – на второй.

Принцип равенства относительных приростов расхода топлива может быть распространен с определенными дополнениями на задачу оптимального распределения активной мощности между отдельными электростанциями ЭЭС.

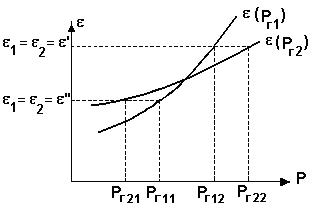
Рис. 2.3. Характеристики относительных приростов расхода топлива

для двух агрегатов

Электростанции в ЭЭС объединены на параллельную работу электрическими сетями. Экономичность режима работы ЭЭС определяется не только суммарным расходом топлива, но и потерями мощности в электрических сетях. Потери активной мощности в сетях зависят от перетоков по ним мощностей, связанных с распределением суммарной нагрузки между отдельными электростанциями. Чем длиннее и загруженнее линии связи между отдельными станциями, тем сильнее влияние потерь мощности в сетях на экономичный режим работы ЭЭС и тем ощутимее поправки к распределению мощностей между станциями, выполненному по условию равенства относительных приростов расхода топлива.

Кроме того, в ЭЭС только с тепловыми станциями часть станций работает по вынужденному графику. К таким станциям относятся, например, городские ТЭЦ, выработка электроэнергии на которых определяется тепловым графиком нагрузки.

Таким образом, вопрос об экономичном распределении активной мощности между станциями ЭЭС следует решать с учетом ряда дополнительных условий, характеризующих работу конкретной ЭЭС.