Интегральный метод Э. Б. Чекалюка

В данном случае основной формулой является

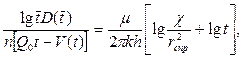(7.18)

где D(t) — интеграл Дюамеля;

Q₀ — дебит скважины до ее остановки;

V(t) —суммарный приток жидкости в скважину к момен­ту времени t после ее закрытия на устье.

Если ввести в уравнение (7.18) коор­динаты ;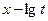

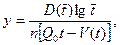(7.19)

где п — масштабный коэффициент, получим прямую линию с угловым коэффициентом

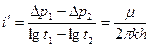(7.20)

и отрезком на оси у

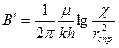(7.21)

Изменение суммарного притока жидкости «в скважину после ее закрытия на устье

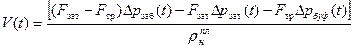, (7.22)

где F_зат, F_тр — площади сечений столбов жидкости в затрубном пространстве и в подъемных трубах, соответственно;

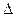р_заб (t), 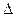р_зат (t), 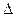р_буф (t) — приращения давления на забое скважины, в затрубном простран­стве и на буфере, начиная от момента ее остановки;

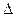
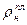— плотность нефти в пласто­вых условиях.

Для построения зависимости (7.18) не­обходимо вычислить координаты трех-четы­рех точек. Предварительно кривая восста­новления давления строится в специальных координатах 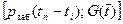в предположении, что исследование скважины длилось заданное время

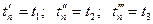
и т. д. Величины G( 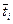) определялись с по­мощью палеток (рис. 7.3), а интеграл Дюамеля — по предыдущим кривым путем графического интегрирования:

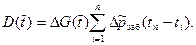(7.23)

Здесь 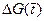— выбранный шаг по оси абс­цисс при определении интеграла.

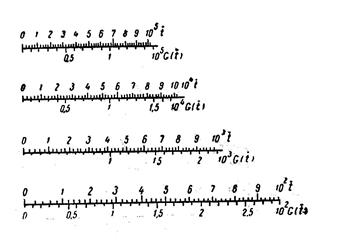
Рис. 7.3. Палетки для определения вспомога­тельной функции.