Задачи и методы расчета размерных цепей.
Прямая (проектная) задача – задача, при которой заданы параметры замыкающего звена (номинальное значение, допустимые отклонения и т.д.) и требуется определить параметры составляющих звеньев.
Обратная (проверочная) задача – задача, в которой известны параметры составляющих звеньев (допуски, поля рассеивания, координаты их середин и т.д.) и требуется определить параметры замыкающего звена.
Метод расчета на максимум-минимум – метод расчета, учитывающий только предельные отклонения звеньев размерной цепи и самые неблагоприятные их сочетания. Метод обеспечивает полную взаимозаменяемость.
Вероятный метод расчета – метод расчета, учитывающий рассеяние размеров и вероятность различных сочетаний отклонений составляющих звеньев размерной цепи.
Метод обеспечивает неполную взаимозаменяемость.
Рассмотрим основные соотношения, используемые для расчета размерных цепей. При этом будем рассматривать линейные размерные цепи, это цепи звенья которых расположены на параллельных прямых. Соотношения для линейных размерных цепей после введения в них передаточных отношений 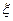 описывают и угловые размерные цепи.
описывают и угловые размерные цепи.
Метод максимума-минимума.
Основное уравнение размерной цепи запишем в виде:
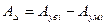 (5)
(5)
Каждый заданный размер имеет три значения: номинальное, максимальное, линейное. Поэтому можно записать:
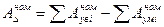 . (6)
. (6)
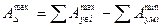 . (7)
. (7)
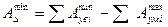 . (8)
. (8)
Вычтем почленно (размеры одного наименования) (8) из (7).
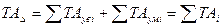 , (9)
, (9)
где Т – допуск; 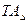 – допуск звена ТА,
– допуск звена ТА, 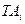 – допуск звена Аi.
– допуск звена Аi.
Таким образом, допуск замыкающего звена равен арифметической сумме допусков составляющих звеньев.
Из (9) можно наметить основные пути повышения точности замыкающего звена:
а) уменьшение допусков составляющих звеньев;
б) сокращение числа звеньев в размерной цепи (принцип короткой цепи).
Для угловой размерной цепи выражение (9) имеет следующий вид:
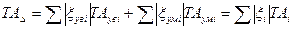 . (10)
. (10)
Выведем формулы для определения предельных отклонений замыкающего звена по предельным отклонениям составляющих звеньев.
Для определения верхнего предельного отклонения из (7) вычитаем (6).
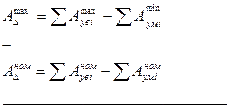
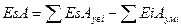 , (11)
, (11)
здесь 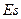 – верхнее предельное отклонение,
– верхнее предельное отклонение, 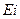 – нижнее предельное отклонение.
– нижнее предельное отклонение.
То есть верхнее предельное отклонение замыкающего звена равняется разности суммы верхних предельных отклонений увеличивающих звеньев и суммы нижних предельных отклонений уменьшающих звеньев.
Для определения нижнего предельного отклонения замыкающего звена из (8) вычитаем (6)
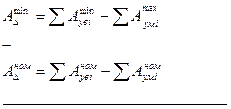
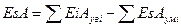 . (12)
. (12)
То есть нижнее предельное отклонение замыкающего звена равняется разности суммы нижних предельных отклонений увеличивающих звеньев и суммы верхних предельных отклонений уменьшающих звеньев.
Предельные отклонения замыкающего звена можно рассчитать и по средним отклонениям составляющих звеньев 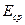 .
.
Среднее отклонение составляющих звеньев определяется по выражению
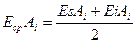 . (13)
. (13)
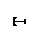
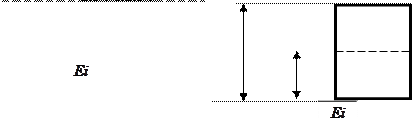
Справедливость этого выражения иллюстрируется на рис.4.
Сложим почленно выражения (11) и (12) и учитывая (13) получим для замыкающего звена:
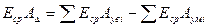 . (14)
. (14)
Из рис.4 ясно, что
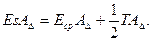 (15)
(15)
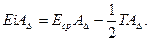 (16)
(16)
Вероятностный метод
Номинальное значение замыкающего звена определяется так же как и в методе максимума-минимума, т.е.
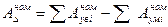 .
.
Поле допуска замыкающего звена определяется по вероятностной формуле:
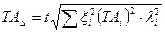 , (17)
, (17)
здесь t – аргумент нормированной функции Лапласа ø(t).
В зависимости от вероятной доли брака (процент риска) принимает следующие значения.




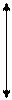

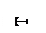

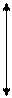

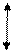




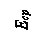

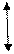
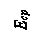
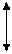
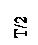
  | |||||||||||
| |||||||||||
| | |||||||||||
| | |||||||||||
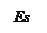 | |||||||||||
|
Рис.4. Схема определения среднего отклонения размера
| Процент риска Р | 4,5 | 1,0 | 0,27 | 0,1 | 0,01 | ||
| t | 1,0 | 1,65 | 2,0 | 2,57 | 3,0 | 3,29 | 3,89 |
Обычно на практике задают Р=0,27%. В этом случае количество деталей, выходящих за пределы допуска не превышает 3 штук на 1000 деталей. При Р=0,27% t=3.
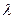 – коэффициент относительного рассеивания размеров.
– коэффициент относительного рассеивания размеров.
При рассеивании размеров по закону Гаусса  ; равной вероятности
; равной вероятности 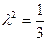 . Симпсон
. Симпсон 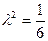 .
.
При расчете по вероятностному методу возникает необходимость использование выражений (14-16).
Практическая часть.
4.Пример 1. Обратная (проверочная) задача размерной цепи.
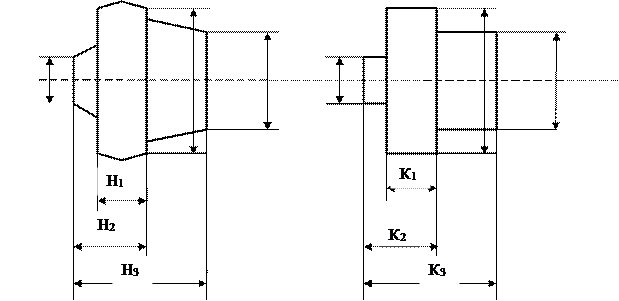
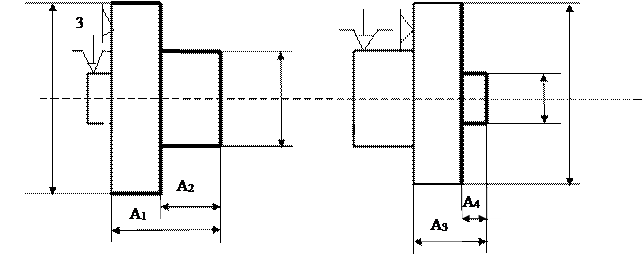
На рис.5 приведен технологический процесс изготовления ступенчатого вала.
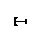
 Наблюдается брак. Требуется проверить припуск, снимаемый при выполнении операционного размера А6 при чистовой подрезке торца в операции 020. Эту задачу решаем в следующей последовательности. Выполняем эскиз совмещенных переходов (ЭСП) следующим образом (рис.6). Вычерчиваем эскиз заготовки, на котором поставляем размеры заготовки. Далее проставляем операционные размеры в порядке их выполнения по операционно по переходам сверху–вниз. Операционные размеры ставим в виде стрелок
Наблюдается брак. Требуется проверить припуск, снимаемый при выполнении операционного размера А6 при чистовой подрезке торца в операции 020. Эту задачу решаем в следующей последовательности. Выполняем эскиз совмещенных переходов (ЭСП) следующим образом (рис.6). Вычерчиваем эскиз заготовки, на котором поставляем размеры заготовки. Далее проставляем операционные размеры в порядке их выполнения по операционно по переходам сверху–вниз. Операционные размеры ставим в виде стрелок 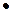 . Точка обозначает измерительную базу, стрелка – обработанную поверхность. При простановки операционных размеров на заготовке вычерчиваем снимаемый припуск. Далее проставляем конструкторские размеры. В нашем примере конструкторский размер К3 совпал с операционным размером А7, конструкторские размеры К1, К2 не совпали с операционными, т.е. они непосредственно не получаются в ходе изготовления. Размеры К1, К2 получаются автоматически в ходе выполнения каких-то операционных размеров.
. Точка обозначает измерительную базу, стрелка – обработанную поверхность. При простановки операционных размеров на заготовке вычерчиваем снимаемый припуск. Далее проставляем конструкторские размеры. В нашем примере конструкторский размер К3 совпал с операционным размером А7, конструкторские размеры К1, К2 не совпали с операционными, т.е. они непосредственно не получаются в ходе изготовления. Размеры К1, К2 получаются автоматически в ходе выполнения каких-то операционных размеров.
Далее строим размерную цепь, в которой проверяемый припуск Z6 является замыкающим звеном, ибо он в ходе обработки непосредственно не выполняется. Итак, определяем Z6, далее определяем операционные размеры примыкающие к Z6 справа и слева. это размеры А6 и А4. Далее определяем размеры, замыкающие размерную цепь кратчайшим путем. Это размеры А3, А5.
Применяя правило обхода по контору, проставляем стрелки на звеньях размерной цепи. Это позволяет записать основное уравнение размерной цепи в виде:
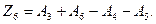





| |







| |

| |


  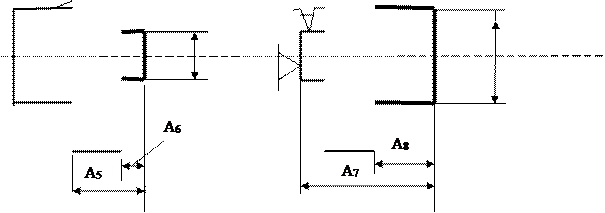 |
 Рис.5 Технологический процесс
Рис.5 Технологический процесс

Рис.6 Эскиз совмещенных переходов (ЭСП)
Определяем номинальное значение 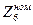 .
.
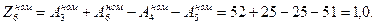
Дальнейшие расчеты будем производить двумя методами: максимума-минимума, вероятным.
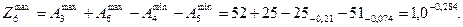
Здесь для определения верхнего предельного отклонения 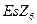 использовано выражение (11).
использовано выражение (11).
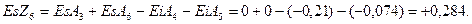
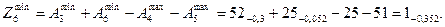
Здесь для определения нижнего отклонения 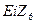 использовано выражение (12)
использовано выражение (12)
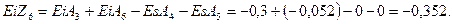
Таким образом, при расчете по методу максимума-минимума, получили:
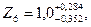
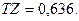
Делаем проверку, должно выполняться
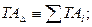
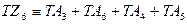
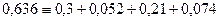
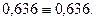
Значит расчеты по методу максимума-минимума выполнены правильно.
Определим поле допуска замыкающего звена вероятным методом. Используем формулу (17).
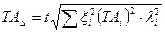 .
.
В качестве примера возьмём: t=3,0;  . Для линейной размерной цепи
. Для линейной размерной цепи 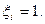 Тогда
Тогда 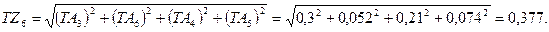
Теперь необходимо определить верхнее и нижнее предельные отклонения замыкающего звена. При использовании вероятного метода расчета вначале определяем среднее отклонение замыкающего звена, т.е. 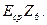 Используем выражение (14).
Используем выражение (14).
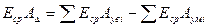 .
.
Тогда 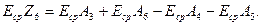
Согласно (13) 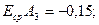
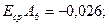
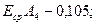
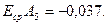
Тогда 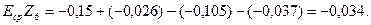
Используя выражения (15) и (16) определяем:
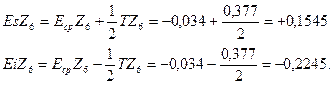
Итак, по вероятному методу
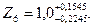
Далее необходимо расчетные значения припуска Z6 сопоставит с табличными значением и сделать анализ.
5.Пример 2.
В рассмотренном ранее технологическом процессе конструктивный размер К1 получается автоматически. Проверить выполняется ли этот размер. Это обратная (проверочная) задача размерной цепи. Решается так же как и пример 1. Размерная цепь имеет вид: 

|
|
|
|





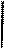

Дано: А6, А7, А8 –
операционные размеры
Проверить: К1
6.Пример 3.
Используем размерную цепь примера 2. Рассмотрим прямую (проектную) задачу размерной цепи.
Дано: К1=25-0,21 – замыкающее звено,
А6=25-0,052; А8=50-0,062 – составляющие звенья.
Определить размер А7 – составляющее звено. Основное уравнение имеет вид:
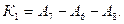
Должно выполняться условие
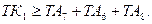 (18)
(18)
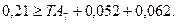
Тогда 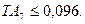
Т.е. условие (18) выполнено.
Если же условие (18) не выполняется, т.о. требуется для обеспечения его выполнения или ужесточать допуски на размеры А6, А8 или расширять допуск размера К1.
Определяем 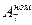 .
.
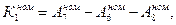 тогда
тогда
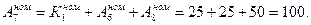
Далее 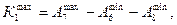 тогда
тогда

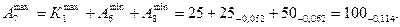
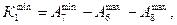 тогда
тогда
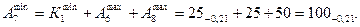
По расчету 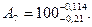
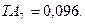
Предельные отклонения гостированные, ближайшее 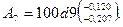
Проверим обеспечивает ли этот размер выполнение размера К1.
Решаем обратную (проверочную) задачу
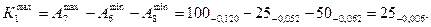
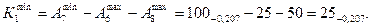
Итак, по расчету 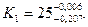
Этот размер обеспечивает выполнение заданного размера 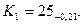
Таким образом, назначаем 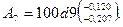
Дата добавления: 2015-03-23; просмотров: 3068;
