КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
1. Скорость  материальной точки.
материальной точки.
Перемещением материальной точки за время 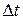 называется вектор
называется вектор  , соединяющий начальное и конечное положение этой точки. Путь
, соединяющий начальное и конечное положение этой точки. Путь  - расстояние, пройденное точкой по траектории за время
- расстояние, пройденное точкой по траектории за время 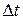 (рис.1).
(рис.1).
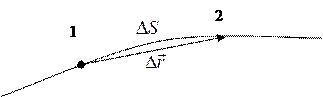 |
Рисунок 1 – Перемещение  и путь
и путь  материальной точки.
материальной точки.
При прямолинейном движении с постоянной скоростью, скорость 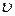 определяется как
определяется как
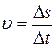 .
.
Если скорость меняет величину или направление, ее можно считать постоянной только на малом промежутке времени 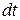 . Поэтому в каждой точке траектории скорость определяется как отношение пути
. Поэтому в каждой точке траектории скорость определяется как отношение пути 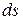 , пройденного за малое время
, пройденного за малое время 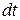 , к этому временному интервалу (т.е. как производная от пути
, к этому временному интервалу (т.е. как производная от пути  по времени
по времени 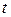 ),
),
 . (1)
. (1)
Соответственно путь  , пройденный за время
, пройденный за время 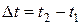 , равен интегралу от скорости
, равен интегралу от скорости 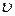 по времени
по времени 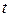
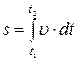 . (2)
. (2)
Скорость - вектор, направленный по касательной к траекториидвижения.
- вектор, направленный по касательной к траекториидвижения.
Расстояние 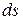 и величина перемещения
и величина перемещения 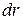 , пройденные за малое время, совпадают,
, пройденные за малое время, совпадают, 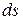 =
= 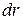 . При
. При 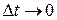 вектор
вектор  , секущий траекторию, становится касательным к ней вектором
, секущий траекторию, становится касательным к ней вектором 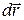 , т.е. направлен по скорости
, т.е. направлен по скорости  . Поэтому в векторном виде скорость записывают как
. Поэтому в векторном виде скорость записывают как
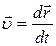 . (3)
. (3)
Средней скоростью движения за время 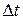 называется величина
называется величина
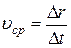 . (4)
. (4)
Движение материальной точки также описывают с помощью ее координат 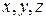 . В этом случае, чтобы определить скорость
. В этом случае, чтобы определить скорость 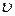 , сначала вычисляют проекции скорости на оси x,y,z , которые равны производным от соответствующих координат по времени
, сначала вычисляют проекции скорости на оси x,y,z , которые равны производным от соответствующих координат по времени
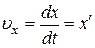 ,
, 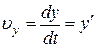 ,
, 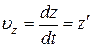 . (5)
. (5)
Тогда величина скорости
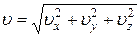 . (6)
. (6)
2. Ускорение 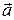 точки.
точки.
Ускорение характеризует быстроту изменения скорости
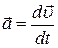 , (7)
, (7)
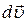 - изменение вектора скорости за малый промежуток времени
- изменение вектора скорости за малый промежуток времени 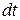 .
.
Ускорение 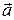 можно разложить на тангенциальное (его еще называют касательным) ускорение
можно разложить на тангенциальное (его еще называют касательным) ускорение 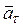 и нормальное (центростремительное) ускорение
и нормальное (центростремительное) ускорение  ,
,
 . (8)
. (8)
Тангенциальное ускорение 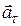 возникает, если скорость меняет величину, оно равно производной от скорости
возникает, если скорость меняет величину, оно равно производной от скорости 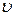 по времени
по времени 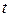 ,
,
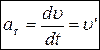 . (9)
. (9)
При движении с постоянной по величине скоростью 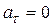 .
.
Нормальное ускорение
 , (10)
, (10)
 - радиус кривизны траектории в данной ее точке. Радиус кривизны
- радиус кривизны траектории в данной ее точке. Радиус кривизны  равен радиусу окружности, дуга которой совпадает с участком траектории.
равен радиусу окружности, дуга которой совпадает с участком траектории.
Для траектории, представляющей собой прямую линию, 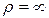 и
и 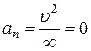 . Т.е. нормальное ускорение возникает только при искривлении траектории движения, когда вектор скорости
. Т.е. нормальное ускорение возникает только при искривлении траектории движения, когда вектор скорости 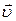 меняет свое направление.
меняет свое направление.
Если траектория точки – окружность, то радиус кривизны равен радиусу окружности,  , и
, и 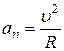 .
.
Тангенциальное ускорение 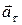 направлено по касательной к траектории; направление
направлено по касательной к траектории; направление 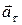 совпадает с направлением вектора скорости
совпадает с направлением вектора скорости  при ускоренном движении и противоположно ему при замедленном. Нормальное ускорение
при ускоренном движении и противоположно ему при замедленном. Нормальное ускорение  перпендикулярно
перпендикулярно 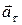 и направлено в сторону вогнутости траектории (рис.2). Т.к. векторы
и направлено в сторону вогнутости траектории (рис.2). Т.к. векторы  и
и 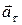 перпендикулярны, то величина полного ускорения
перпендикулярны, то величина полного ускорения
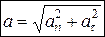 . (11)
. (11)
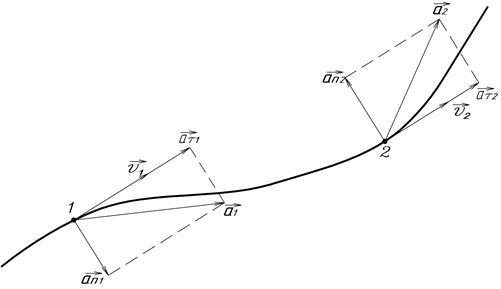
Рисунок 2 – Направление векторов скорости и ускорения.
При координатном способе задания движения, чтобы определить ускорение, сначала вычисляют его проекции на оси x,y,z
 ,
, 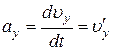 ,
,  . (12)
. (12)
Величина ускорения в этом случае
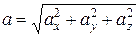 . (13)
. (13)
Дата добавления: 2015-03-20; просмотров: 783;
