Прийняття фінансових рішень за умов ризику
Фінансові рішення — рішення щодо визначення обсягу та структури інвестованих коштів (власних і позикових), забезпечення поточного фінансування наявних коротко- та довгострокових активів (структура власних засобів, позикових засобів, сполучення коротко- та довгострокових джерел). Прикладом чисто фінансових рішень є вибір: схеми створення й обігу фінансових активів; форми одержання прибутку та подальшого реінвестування чи споживання. Інвестиційні рішення, як правило, взаємозалежні з фінансовими, але можуть прийматися без останніх. Фінансові рішення змінюють оцінку активу та роблять його більш інвестиційно привабливим.
Важливу роль в управлінні інвестиціями відіграє теорія оптимального портфеля, пов’язана з проблемою вибору ефективного портфеля, що максимізує очікувану дохідність за певного, прийнятного для інвестора, рівня ризику. Портфелем цінних паперів називається сукупність активів (акцій, облігацій), складених у найбільш вигідних пропорціях. Структура портфеля — співвідношення часток різних видів інвестицій у цінні папери, вартість портфеля — це вартість усіх паперів у його складі [31]. Під прибутковістю портфеля за визначений період (рік) мається на увазі величина:
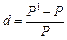 , (6.11)
, (6.11)
де P — сьогоднішня вартість портфеля, P1 — вартість портфеля через рік.
Інвестування коштів пов’язане з великим ризиком. Найризикованішим портфелем є портфель акцій, тому що акції не належать до цінних паперів із фіксованим доходом (за винятком привілейованих).
Формуючи інвестиційний портфель акцій, інвестори намагаються за мінімального ризику отримати максимальний прибуток. Основні принципи роботи на ринку цінних паперів відповідають розумній диверсифікації коштів — процесу розподілу інвестованих коштів між різними об’єктами вкладення капіталу для зниження ступеня ризику, забезпечення більшої стійкості доходів за будь-яких коливань дивідендів і ринкових цін на цінні папери. Загальне правило інвестора щодо диверсифікації — необхідно прагнути розподілити вкладення між такими видами активів, які показали за минулі роки: різну щільність зв’язку (кореляцію) із загальноринковими цінами (індексами); протилежну фазу коливання норм прибутку (цін) усередині портфеля.
Формування структури портфеля цінних паперів, яка приносить найбільший дохід, є дуже складним завданням, розв’язанням якого займалося багато економістів. Гаррі Марковіц уважається «батьком» сучасної «портфельної теорії», яка стосується методів збалансування ризиків та економічного зиску у виборі ризикованих інвестицій [58]. Р. Тобін збагатив ідею Г. Марковіца пропозицією включати в портфель поряд з ризиковими безризикові папери, щоби зменшити ризик усього портфеля (чим більше таких паперів у портфелі, тим менший ризик, але й менший можливий дохід).
Основна ідея теорії: структура портфеля цінних паперів має повторювати структуру великого ринку цінних паперів. Принцип ринкової рівновагі ґрунтується на розумінні того факту, що ринок цінних паперів в умовах ринкової економіки є добре збалансованою системою. Це значить, що розрив між цінами попиту та пропонування незначний. Звідси випливають важливі висновки: середньоринковій прибутковості відповідає мінімально можливий ступінь ризику; максимально можливий дохід досягається за структури портфеля, ідентичній структурі ринкового обороту. Таким чином, для того, щоб інвестору сформувати портфель цінних паперів з найменшим ризиком і найбільшою прибутковістю, необхідно відтворити в ньому структуру ринку (з періодичним її коригуванням).
Розглянемо принципи постановки задач формування оптимальних портфелів цінних паперів Марковіца й Тобіна. Для цього введемо кілька позначень: 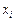 — частка паперів і-го виду в портфелі,
— частка паперів і-го виду в портфелі,  ;
; 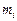 — математичне очікування прибутковості і-го виду паперів,
— математичне очікування прибутковості і-го виду паперів, 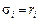 — ризик і-го виду паперів (середньоквадратичне відхилення прибутковості). Прибутковість портфеля
— ризик і-го виду паперів (середньоквадратичне відхилення прибутковості). Прибутковість портфеля 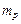 можна розглядати як середньозважену величину від дохідностей паперів, що його утворюють:
можна розглядати як середньозважену величину від дохідностей паперів, що його утворюють:
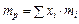 . (6.10)
. (6.10)
Як правило, і середня ринкова прибутковість визначається як середньозважена прибутковість усіх акцій ринку. Цей показник розраховують за акціями найбільш представницьких компаній. Індексів, застосовуваних у міжнародній практиці, досить багато. У США, наприклад, дуже представницьким вважається індекс компанії «Standart and Poors», розрахований за акціями 500 найбільших компаній. Оскільки одночасно максимізувати ефективність і мінімізувати ризик не можна, то доводиться оптимізувати щось одне, накладаючи обмеження на інший параметр [31].
Портфелі мінімального ризику формуються через вимогу мінімізації ризику за умови обмеження на прибутковість. Портфель Тобіна від портфеля Марковіца відрізняється тим, що в нього включені безризикові цінні папери.
Портфель мінімального ризику:
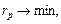
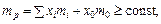 (6.11)
(6.11)

де 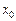 — частка капіталу, вкладеного в безризикові цінні папери,
— частка капіталу, вкладеного в безризикові цінні папери, 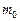 — ефективність безризикових цінних паперів.
— ефективність безризикових цінних паперів.
Портфелі максимальної ефективності формуються через вимогу максимізації прибутковості за умови обмеження на ризик. Портфель Тобіна відрізняється тим, що в нього включені безризикові цінні папери.
Портфель максимальної ефективності:
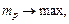
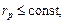 (6.12)
(6.12)
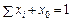 .
.
Реально портфелі Марковіца і Тобіна — абстракції, тому що для кожного папера, що обертається на ринку, неможливо вірогідно знати ні його дохідності, ні середньоквадратичного відхилення. Крім того, хоч би яким великим був портфель окремого інвестора, він не в змозі повторити структуру ринку внаслідок розрахункової мізерності часток багатьох видів акцій, необхідних для його складання. Такий спосіб формування портфеля акцій при-
йнятний лише до певної міри і лише для великих гравців на фондових біржах. Тому для практичних цілей пропонуються рішення у вигляді рекомендаційних порад. Вважається, що стійкий до коливань ринку пакет акцій складається як мінімум із цінних паперів 12 різних компаній. Приблизно третина акцій має придбаватися у великих і найбільших компаній, третина — у середніх і третина — у швидко зростаючих невеликих фірм. Відомо також «правило п’яти пальців руки», за яким з кожних п’яти акцій у пакеті одна завдасть збиток, три більш-менш принесуть очікувані дивіденди, а одна дасть значно кращі результати, ніж очікувалося. З огляду на це часто мінімальною кількістю різних видів акцій в оптимальному портфелі вважається число «п’ять» [31].
Ризикованість одного активу вимірюється дисперсією, або середньоквадратичним відхиленням доходів за цим активом, а ризик портфеля — дисперсією, або середньоквадратичним відхиленням доходів портфеля. Для визначення стандартного відхилення портфеля користуються коваріацією — статистичною мірою взаємодії двох випадкових змінних. Тобто це міра того, наскільки дві випадкові величини (наприклад, дохідності двох цінних паперів), залежать одна від одної. Додатне значення показника коваріації показує, що дохідності цих паперів мають тенденцію змінюватися в один бік, від’ємне значення свідчить про те, що дохідності мають тенденцію компенсувати одна одну. Відносно невелике або нульове значення коваріації показує те, що зв’язок між дохідністю цих паперів слабкий або відсутній зовсім. Коваріацію кожної пари активів можна знайти за формулою:
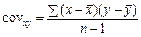 . (6.13)
. (6.13)
Формування оптимального портфеля з обмеженої кількості цінних паперів [31]
Ефективність цінного папера Rt, або норма прибутку в t-му періоді визначається формулою:
 , (6.14)
, (6.14)
де P(t) — ціна папера наприкінці t-го періоду;P(t – 1) — ціна папера наприкінці t – 1-го періоду; D(t) — дивіденди, нараховані в t-му періоді.
Випадкову величину ефективності j-го виду цінних паперів позначимо через Rj. Очікувану ефективність j-го ЦП позначимо через mp, варіацію — Vj, коваріацію між Ri і Rj — Vij. Нехай  — частка загального вкладення, що припадає на j-й вид ЦП так, що
— частка загального вкладення, що припадає на j-й вид ЦП так, що 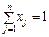 . Тоді очікувана ефективність портфеля
. Тоді очікувана ефективність портфеля 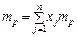 , а дисперсія ефективності
, а дисперсія ефективності  . Математична модель знаходження оптимального портфеля має такий вигляд:
. Математична модель знаходження оптимального портфеля має такий вигляд:
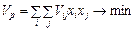 , (6.15)
, (6.15)
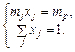 (6.16)
(6.16)
Задача полягає у знаходженні xp, які мінімізують варіацію портфеля Vp за умови, що гарантується задане значення mp очікуваної ефективності. Прийнято розглядати два випадки: xj ≥ 0 і xj довільного знака (або розміщене в деякому проміжку). Якщо xj ≤ 0, то це означає, що папери j-го виду рекомендується взяти в борг або взяти в борг гроші під відсоток mj (допускається short sale) для формування необхідного портфеля. У випадку допустимості short sale розв’язання набуває такого вигляду:
 , (6.17)
, (6.17)
де
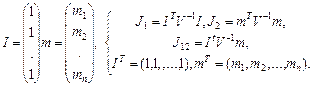 (6.18)
(6.18)
У випадку, якщо на ринку цінних паперів є безризикові цінні папери, структура ризикової частини в оптимальному портфелі постійна. Тому за наявності цих паперів інвестор на свій розсуд (у міру схильності до ризику) вибирає, яку частину капіталу вкласти в безризикові, а яку — в ризикові. При цьому структура ризикової частини визначається однозначно, незалежно від схильності інвестора до ризику. Нехай є безризикові цінні папери з ефективністю r0. Якщо задається mp, то структура оптимального портфеля у випадку допустимості short sale визначається формулою:
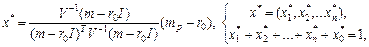 (6.19)
(6.19)
де x0 — частка безризикових цінних паперів.
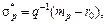
де 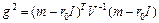
чи 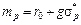 . (6.20)
. (6.20)
Структуру ризикової частини обчислюють за формулою:
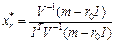 ;
; 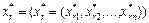 . (6.21)
. (6.21)
При цьому
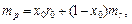 (6.22)
(6.22)
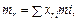
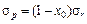 .
.
У випадку двох ЦП вираз істотно спрощується:
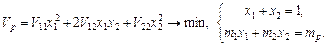 (6.23)
(6.23)
Зокрема, якщо другий ЦП безризиковий, то
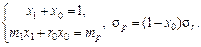 (6.24)
(6.24)
Дата добавления: 2015-03-20; просмотров: 1186;
