Управление временем
Сетевое планирование служит для составления рационального плана решения производственной задачи, предусматривающего осуществление его в кратчайший срок и с минимальными затратами.
Методы сетевого планирования дают возможность оценивать «узкие» места выполняемой задачи и вносить необходимые коррективы в организацию решения.
Сетевое планирование рассмотрим на следующем примере. Производственная задача решается в три этапа (I, II и III). Исходным моментом является получение директором предприятия задания (заказа). Далее на основании этого задания под руководством заместителя директора по производству разрабатываются задания подразделениям № 1 и № 2. После этого подразделения одновременно приступают к I этапу работы. Для того чтобы начать II этап работы, подразделение № 2 должно получить комплект изделий, изготовленных подразделением № 1 в ходе I этапа. Поэтому подразделение № 1 начинает II этап работы сразу же после окончания I этапа, а подразделение № 2– лишь после получения комплектующих из подразделения № 1. Далее роли подразделений меняются: для того чтобы начать III этап, теперь уже подразделение № 1 должно ожидать комплектующих от подразделения № 2. С окончанием III этапа работы обоими подразделениями изделие считается готовым. Транспортная служба доставляет его потребителю.
Все мероприятия решаемой задачи в их взаимосвязи представляются в виде наглядной схемы – сетевого графика (рис. 7.6), состоящего из двух типов элементов – работ и событий.
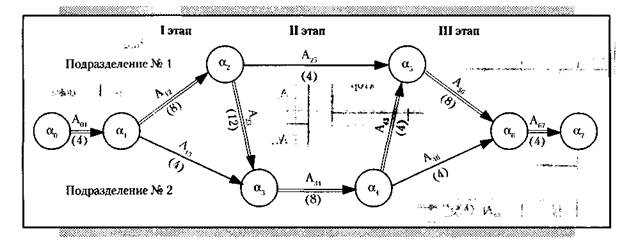
Рис. 7.6.Схема сетевого графика
Работа представляет собой выполнение некоторого мероприятия, например выполнение определенной технологической, транспортной или складской операции. Работа связана с затратой времени и расходом ресурсов, она должна иметь начало и конец. Работа обозначается на графике стрелкой, над которой проставлен номер работы (большая буква с индексом), а под ней – продолжительность работы (в скобках).
Событиями называются начальные и конечные точки работы, например начало или окончание производственной операции. Событие не является процессом и поэтому не сопровождается затратами времени или ресурсов. Событие обозначается кружком с буквенным обозначением внутри (маленькая буква с индексом).
Относительно данной работы события могут быть предшествующими (непосредственно перед ней) и последующими (непосредственно за ней). Относительно данной работы другие работы могут быть предшествующими и последующими. Каждая входящая в данное событие работа является предшествующей каждой выходящей работе; каждая выходящая работа является последующей для каждой входящей.
Основные свойства сетевого графика:
ни одно событие не может произойти до тех пор, пока не будут закончены все входящие в него работы;
ни одна работа, выходящая из данного события, не может начаться до тех пор, пока не произойдет данное событие;
ни одна последующая работа не может начаться раньше, чем будут закончены все предшествующие ей работы.
Приступая к построению сетевого графика, разрабатывают перечень событий, определяющих планируемый процесс – производственную задачу, без которых она не может состояться (табл. 7.11). Затем предусматриваются работы, в результате которых все необходимые события должны произойти (табл. 7.12).
Таблица 7.11
| Обозначение события | Наименование события | Ответственное лицо |
| a0 | Получено задание предприятием | Директор |
| a1 | Разработаны задания подразделениям № 1 и № 2 | Заместитель директора по производству |
| a2 | Выполнена работа I этапа в подразделении № 1 | Начальник подразделения № 1 |
| a3 | Выполнена работа I этапа в подразделении № 2. Подразделением № 2 получены комплектующие из подразделения № 1 | Начальник подразделения № 2 |
| a4 | Выполнена работа II этапа в подразделении № 2 | Начальник подразделения № 2 |
| a5 | Выполнена работа II этапа в подразделении № 1. Подразделением № 1 получены комплектующие из подразделения № 2 | Начальник подразделения № 1 |
| a6 | Выполнены работы III этапа в подразделениях № 1 и №2. Заказ готов. | Начальники подразделений № 1и № 2 |
| a7 | Изделие доставлено потребителю | Начальник транспортной службы |
Таблица 7.12
| Обозначение работы | Наименование работы | Продолжительность выполнения работы, ч |
| А01 | Разработка заданий подразделениям № 1 и № 2 | |
| А12 | Выполнение работ I этапа в подразделении № 1 | |
| А13 | Выполнение работ I этапа в подразделении № 2 | |
| А23 | Передача комплектующих из подразделения № 1 в подразделение № 2 | |
| А25 | Выполнение работ II этапа в подразделении № 1 | |
| А34 | Выполнение работ II этапа в подразделении № 2 | |
| А45 | Передача комплектующих из подразделения № 2 в подразделение № 1 | |
| А46 | Выполнение работ III этапа в подразделении № 1 | |
| А56 | Выполнение работ III этана в подразделении № 2 | |
| А67 | Доставка заказа потребителю |
Исходя из перечня событий и работ составляется сетевой график (см. рис. 7.6). Вначале это можно сделать схематично, без учета масштаба времени. Сетевой график строится от исходного события к завершающему, слева направо. Исходному событию присваивается нулевой номер, завершающему событию – последний номер. Остальные события нумеруются так, чтобы номер предыдущего события был меньше номера последующего события.
Работа кодируется индексом, содержащим номера событий, между которыми она заключена. Совершение события зависит от окончания самой длительной из всех входящих в него работ. Последовательные работы и события формируют пути (цепочки), которые ведут от исходного к завершающему событию.
Далее сетевой график строится в масштабе времени (рис. 7.7).
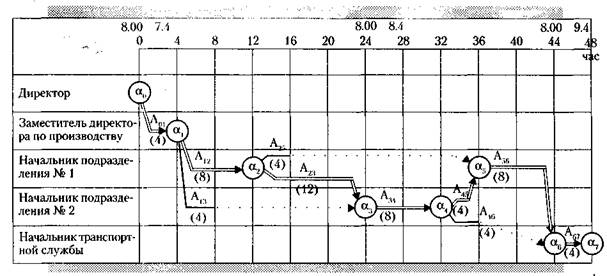
Рис. 7.7.Сетевой график в масштабе времени
Сетевой график дает возможность оценить количество и качество мероприятий планируемой производственной задачи. Он позволяет установить, от каких из них и в какой степени зависит достижение конечной цели действий. Так, ранг события показывает, какое количество работ необходимо выполнить, чтобы данное событие состоялось. Сетевой график также показывает, какое мероприятие следует выполнять в первую очередь, какие можно выполнять параллельно. Так, в нашем примере видно, что ни одна последующая работа не может выполняться раньше, чем закончатся все предшествующие. Видно также, что работы А25 и A23 могут выполняться параллельно.
После построения сетевого графика производится его анализ. Для этого строится так называемый критический путь. Это полный путь, на котором суммарная продолжительность работ является максимальной. Иными словами, это самый длинный по времени путь в сетевом графике от исходного до завершающего события. Критический путь лимитирует выполнение задачи в целом, поэтому любая задержка на работах критического пути увеличивает время всего процесса. На рис. 7.6 и 7.7 критический путь обозначен двойной линией.
Сущность анализа сетевого графика заключается в том, что выявляются резервы времени работ, лежащих вне критического пути, и направляются на работы, лежащие на критическом пути, который лимитирует срок завершения работы в целом. В нашем примере продолжительность работ, лежащих на критическом пути, равна 4 + 8 + 12 + 8 + 4 + 8 + 4 = 48 часов.
Это и есть общее время решения всей производственной задачи.
На рис. 7.7 видно, что в подразделениях № 1 и № 2 появляются отрезки времени, на которых эти подразделения остаются без работы (волнистые линии). В этих случаях целесообразно снять отсюда часть трудовых и технических ресурсов и передать их тому подразделению, работа которого лежит в это время на критическом пути и лимитирует тем самым конечный результат. Так, например, после того как подразделение № 2 в момент, соответствующий 8-му часу работы, выполнит этап I, ему целесообразно передать часть своих ресурсов подразделению № 1 с расчетом, чтобы к событию a3 подразделения № 1 и № 2 подошли одновременно. Для этого нужно передать из подразделения № 2 в подразделение № 1 ровно столько ресурсов, чтобы сократить сумму работ А12 и А23, в подразделении № 1 на 8 часов, то есть до 12 часов. При этом подразделение № 2, лишенное части ресурсов, увеличит время своей работы на эти же 8 часов (работа А13, станет равна 12 часам) и критический путь между событиями a3 и a2 будет равен 12 часам. Это сокращение общего времени критического пути означает и сокращение на то же время – на 8 часов – продолжительности решения всей производственной задачи.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое решение?
2. Что такое управленческое решение?
3. Как классифицируются управленческие решения?
4. Что понимается под исследованием операций?
5. Что такое моделирование ситуации?
6. Что такое модель?
7. Как классифицируются модели?
8. Какие бывают модели производственно-экономической системы?
9. Какие бывают модели управления производством?
10. Что такое игровое моделирование?
11. Что включает процесс подготовки и принятия решения?
12. Опишите этапы процесса принятия решения.
13. Опишите выбор наилучшего (оптимального) варианта решения задачи.
14. Опишите модель производственно-экономической ситуации.
15. Какие моменты психологического характера влияют на принятие решения?
16. Опишите станковую задачу.
17. Опишите задачу раскроя материала.
18. Опишите задачу управления очередями.
19. Опишите задачу о назначениях.
20. Опишите задачу сетевого планирования.
Дата добавления: 2015-03-20; просмотров: 1108;
