Градации яркости

Обычно изображение, передаваемое по ТВ, является полутеневым. Это означает, что, кроме ярких и темных мест, соответствующих В_макс и В_мин, в изображении еще имеется много промежуточных градаций яркости, так называемых полутеней. Наличие большого количества этих полутеней делает изображение более художественным, живым и сочным и увеличивает разборчивость очертаний. Поэтому правильная передача градаций яркости является важным фактором в создании высококачественного ТВ изображения. Бывают случаи, когда нет необходимости в передаваемом изображении иметь полный набор градаций яркости, когда можно обойтись только двумя крайними значениями яркости: В_макс и В_мин. К таким случаям можно отнести, например, передачу надписей (черные буквы на светлом фоне), технических чертежей и пр. Но передачи из студии, передачи художественных фильмов и т. п. обязательно требуют хорошего воспроизведения полутеней.

Передача и воспроизведение большого числа градаций связаны с повышением требований к ТВ аппаратуре. Поэтому существенно выяснить предельное число различимых градаций, превышение которого приводит только к усложнению аппаратуры без улучшения качества изображения. Как и во многих других случаях, прибором, определяющим разумную границу максимального числа градаций яркости, является человеческий глаз.

Для того чтобы определить максимальное число градаций, надо найти тот порог, при котором человек замечает разницу в двух соседних значениях яркости. Представим себе два смежных светящихся поля (рис. 2.18.а). Перед этими полями находится группа зрителей. В начале опыта В₁=В₂. Затем при постоянной, например, яркости В₁ будем медленно изменять яркость В₂. Зрители независимо друг от друга, не сговариваясь, должны сообщить момент, когда каждый из них заметил, что В₂ стала отличаться от В₁.

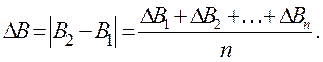
Таким образом, определяется минимальная величина, при которой зритель замечает разницу в этих двух яркостях (здесь DВ_n – индивидуальные показания зрителей, а n – число зрителей).

Подобные опыты проводились неоднократно, и они установили с очевидностью следующий для практики факт: минимальная величина приращения яркости DВ зависит от величины начальной яркости В₁. Чем больше В₁, тем больше оказывается DВ = çВ₂ – В₁ê. Поясним это обстоятельство примером. ТВ экран имеет яркость 40 кд /м² (на белом). Для того чтобы было хотя бы чуть-чуть заметно увеличение (или уменьшение) этой яркости, ее нужно будет изменить на 0,8кд/м², т. е. яркость в 40,8 кд/м² или 39,2 кд/м² будет на глаз едва заметно отличаться от яркости в 40 кд/м². Яркость лампы накаливания составляет 5×10⁶ кд /м². Изменение этой яркости на 0,8 кд/м² никак не будет заметно на глаз. Чтобы получить ощущение хотя бы небольшого изменения яркости, в этом случае DВ должно составлять 2,5×10⁵ кд /м².

	Рис. 2.6.4. Контрастная чувствительность глаза: а) два соседних испытательных поля разной яркости; б) график зависимости контрастной чувствительности от яркости

Экспериментами установлен следующий закон (закон Фехнера):

∆В/В= δ ≈ const , (2.21)

где DВ – приращение яркости, едва заметное на глаз; В – начальная яркость; d - контрастная чувствительность глаза.

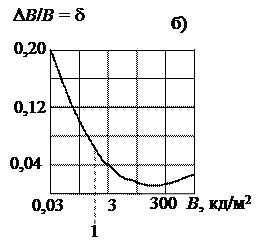
Контрастная чувствительность глаза мало меняется в широком диапазоне яркостей. На рис. 2.18,б представлен график зависимости контрастной чувствительности глаза от яркости наблюдаемого источника. Для яркостей, наблюдающихся на экране телевизора (примерно от 40 до 1 кд/м²), - контрастная чувствительность меняется от 0,05 до 0,02, т. е. в среднем d_ср»0,03.

		Рис. 2.19. К определению числа градаций яркости

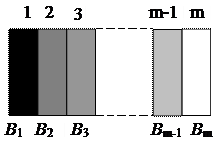
Чтобы подсчитать максимальное число различимых градаций яркости на экране кинескопа, представим себе изображение в виде полос с постепенно увеличивающейся яркостью (рис. 2.19), причем яркость каждой полосы отличается от соседней на минимальную величину DВ, определяемую контрастной чувствительностью глаза d.

Будем считать контрастность изображения b = В_макс /В_мин заданной. Яркость первой полосы В₁ = В_мин, второй полосы В₂ = В₁ + DВ₁ =В₁+dВ₁=В₁(1+d),

третьей полосы В₃ = В₂ + DВ₂ = В₂ + dВ₂ =В₂(1 + d) = В₁(1 + d)²,

m-й полосы В_m = В_m(1 + d)^m-1.

Имея в виду, что В₁ = В_мин, а В_m = В_макс, то получим: β=В_макс/В_мин=(1+δ)^m-1,

откуда: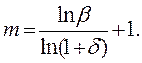

При d<<1 (в нашем случае d =0,02¸0,05) ln(1+d) » d. Кроме того, используя связь между натуральным и десятичным логарифмом lnx = 2,31gx, получим:

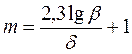. (2.22)

Максимальное число градаций яркости m, различимых глазом, оказывается прямо пропорционально логарифму контрастности b и обратно пропорциональным контрастной чувствительности d.

Приняв для телевидения b = 10 ¸ 40, а d = 0,03. Получаем

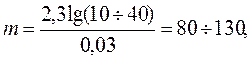
т. е. в среднем около 100.

Мы до сих пор рассуждали о минимально заметном приращении яркости. При любом изменении яркости соответствующее изменение ощущения в сознании человека определяется хорошо подтверждаемым экспериментами законом Вебера – Фехнера. Подходя в определенной степени формально, запишем закон Фехнера [выражение (2.23)] в виде бесконечно малых приращений: 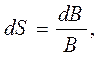(2.23)

где dS – бесконечно малое приращение ощущения. Проинтегрируем правую и левую части выражения (2.6.12.):

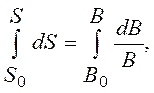т. е. 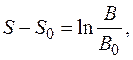(2.24)

где В₀ – начальное значение яркости; В – значение яркости после ее изменение; S₀ – первоначальное ощущение; S – ощущение после изменения яркости.

Формула (2.24) и называется законом Вебера – Фехнера. Согласно этому закону ощущение пропорциональности логарифму яркости.

График зависимости S = ¦(B), построенный на основании формулы (2.24), представлен на рис. (2.20)

Этот график, хорошо согласующийся с практикой, показывает, что между яркостью и вызываемом в зрительном аппарате человека ощущением нет прямой пропорциональности. По мере увеличения яркости ощущение растет все медленнее и медленнее. Это замечательное свойство зрения играет большую роль в повседневной жизни человека. Поясним это обстоятельство примером. Яркость, слабо различимая человеческим глазом, составляет примерно В_мин » 0,01 кд /м². Слепящая яркость, которую еще можно с трудом терпеть (нить лампы накаливания), В_макс=10⁷кд/м². Таким образом, полный динамический диапазон видимых яркостей составит В_макс/В_мин=10⁷/10^-1=10⁸. Было бы немыслимо такой диапазон яркостей (сто миллионов раз) уложить в сознании человека в случае прямой пропорциональности между ощущением и соответствующей ему яркостью. Особенность зрения, подчиняющаяся логарифмическому закону Вебера – Фехнера, как бы сжимает этот гигантский диапазон в сознании человека. По формуле (2.24) ощущение меняется только в 18 раз: ln10⁷/10^-1 = 18,4.