Ранг градации
Рис. 4.4. Пример неравномерного распределения ответов по шкале
Аналогичная картина наблюдается и в том случае, когда респонденту предлагают шкалу, имеющую слишком большую дробность: будучи не в состоянии оперировать всеми градациями шкалы, респондент выбирает лишь несколько базовых. Например, зачастую десятибалльную шкалу респонденты расценивают как некоторую модификацию пятибалльной, предполагая, что «десять» соответствует «пяти», «восемь» — «четырем», «пять» — «трем» и т.д. При этом базовые оценки используются значительно чаще, чем другие.
 Для выявления указанных аномалий равномерного распределения по шкале можно предложить следующее правило: для достаточно большой доверительной вероятности (1—α ³ 0,99) и, следовательно, в достаточно широких границах наполнение каждого значения не должно существенно отличаться от среднего из соседних наполнений. Для чего используется критерий хи-квадрат [19].
Для выявления указанных аномалий равномерного распределения по шкале можно предложить следующее правило: для достаточно большой доверительной вероятности (1—α ³ 0,99) и, следовательно, в достаточно широких границах наполнение каждого значения не должно существенно отличаться от среднего из соседних наполнений. Для чего используется критерий хи-квадрат [19].
Определениегрубых ошибок. В процессе измерения иногда возникают грубые ошибки, причиной которых могут быть неправильные записи исходных данных, плохие расчеты, неквалифицированное использование измерительных средств и т. п. Это обнаруживается в том, что в рядах измерений попадаются данные, резко отличающиеся от совокупности всех остальных значений. Чтобы выяснить, нужно ли эти значения признать грубыми ошибками, устанавливают критическую границу, так чтобы вероятность того, что крайние значения превысят ее, была бы достаточно малой и соответствовала бы некоторому уровню значимости а. Это правило основано на том, что появление в выборке чрезмерно больших значений хотя и возможно как следствие естественной вариабельности значений, но маловероятно.
Если окажется, что какие-то крайние значения совокупности принадлежат ей с очень малой вероятностью, то такие значения признаются грубыми ошибками и исключаются из дальнейшего рассмотрения, Выявление грубых ошибок особенно важно проводить для выборок малых объемов: не будучи исключенными из анализа, они существенно искажают параметры выборки. Для этого используются специальные статистические критерии определения грубых ошибок [19].
Итак, дифференцирующая способность шкалы как первая существенная характеристика ее надежности предполагает: обеспечение достаточного разброса данных; выявление фактического использования респондентом предложенной протяженности шкалы; анализ отдельных «выпадающих» значений; исключение грубых ошибок. После того как установлена относительная приемлемость используемых шкал в указанных аспектах, следует переходить к выявлению устойчивости измерения по этой шкале.
Существует несколько методов оценки устойчивости измерений: повторное тестирование; включение в анкету эквивалентных вопросов и разделение выборки на две части.
Метод повторного тестирования был охарактеризован выше.
Часто интервьюеры в конце опроса частично его повторяют, говоря при этом: «Заканчивая нашу работу, вновь коротко пройдемся по вопросам анкеты, чтобы я мог проверить, все ли я правильно записал из ваших ответов». Конечно, речь идет не о повторении всех вопросов, а только критических из их числа. При этом надо помнить, что если интервал времени между тестированием и повторным тестированием слишком короткий, то респондент просто может помнить первоначальные ответы. Если интервал слишком велик, то могут иметь место некоторые реальные изменения.
Включение в анкету эквивалентных вопросов предполагает использование в одной анкете вопросов по той же проблеме, но сформулированных по-другому. Их респондент должен воспринимать как разные вопросы. Главная опасность данного метода заключается в степени эквивалентности вопросов; если это не достигается, то респондент отвечает на разные вопросы.
Разделение выборки на две части основано на сравнении ответов на вопросы двух групп респондентов. Предполагается, что эти две группы являются идентичными по своей композиции и что средние оценки ответов для этих двух групп являются очень близкими. Все сравнения делаются только на групповой основе, поэтому сравнение внутри группы проводить невозможно. Например, среди студентов колледжа с помощью модифицированной шкалы Лайкерта с пятью градациями был проведен опрос относительно их будущей карьеры. В анкете приводилось утверждение: «Я считаю, что меня ожидает блестящая карьера». Ответы были обобщены, начиная с «сильно не согласен» (1 балл) и кончая «сильно согласен» (5 баллов). Затем общая выборка опрошенных была разделена на две группы и были вычислены средние оценки для этих групп. Средняя оценка была одинаковой для каждой группы и равнялась 3-м баллам. Данные результаты дали основание считать измерение надежным. Когда же групповые ответы были проанализированы более внимательно, то оказалось, что в одной группе все студенты ответили «и согласен и не согласен», а в другой — 50% ответили «сильно не согласен», а другие 50% — «сильно согласен». Как видно, более глубокий анализ показал, что ответы не являются идентичными.
Вследствие данного недостатка этот метод оценки устойчивости измерений является наименее популярным.
О высокой надежности шкалы можно говорить лишь в том случае, если повторные измерения при ее помощи одних и тех же объектов дают сходные результаты. Если устойчивость проверяют на одной и той же выборке, то часто оказывается достаточным сделать два последовательных замера с определенным временным интервалом — таким, чтобы этот промежуток не был слишком велик, чтобы сказалось изменение самого объекта, но и не слишком мал, чтобы респондент мог по памяти «подтягивать» данные второго замера к предыдущему (т. е. его протяженность зависит от объекта изучения и колеблется от двух до трех недель).
Существуют различные показатели оценки устойчивости измерений. Среди них чаще всего используется средняя квадратическая ошибка (см. ниже).
До сих пор речь шла об абсолютных ошибках, размер которых выражался в тех же единицах, что и сама измеряемая величина. Это не позволяет сравнивать ошибки измерения разных признаков по разным шкалам. Следовательно, помимо абсолютных, нужны относительные показатели ошибок измерения.
В качестве показателя для нормирования абсолютной ошибки можно использовать максимально возможную ошибку в рассматриваемой шкале (xmax).
Если число делений шкалы k, тогда xmax, равное разнице между крайними значениями шкалы (xmax — xmin), будет k — 1 и относительная ошибка окажется такой:
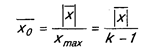
(здесь х — средняя арифметическая ошибка измерения).
Однако зачастую этот показатель «плохо работает» из-за того, что шкала не используется на всей ее протяженности. Поэтому более показательными являются относительные ошибки, рассчитанные по фактически используемой части шкалы.
Если число градаций в «работающей» части шкалы обозначить k1, то тогда
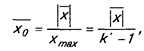
а если в качестве абсолютной ошибки использовалась средняя квадратическая ошибка S, то показатель относительной ошибки
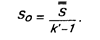
Дляповышения устойчивости измерения необходимо выяснить различительные возможности пунктов используемой шкалы, что предполагает четкую фиксацию респондентами отдельных значений: каждая оценка должна быть строго отделена от соседней. На практике это означает, что в последовательных пробах респонденты четко повторяют свои оценки. Следовательно, высокой различимости делений шкалы должна соответствовать малая ошибка.
Эту же задачу можно описать в терминах чувствительности шкалы, которая характеризуется количеством делений, приходящихся на одну и ту же разность в значениях измеряемой величины, т. е. чем больше градаций в шкале, тем больше ее чувствительность. Однако чувствительность нельзя повышать простым увеличением дробности, ибо высокая чувствительность при низкой устойчивости является излишней (например, шкала в 100 баллов, а ошибка измерения ±10 баллов).
Но и при малом числе градаций, т. е. при низкой чувствительности, может быть низкая устойчивость, и тогда следует увеличить дробность шкалы. Так бывает, когда респонденту навязывают категорические ответы «да», «нет», а он предпочел бы менее жесткие оценки. И потому он выбирает в повторных испытаниях иногда «да», иногда «нет».
Итак, следует найти некоторое оптимальное соотношение между чувствительностью и устойчивостью. Рекомендуется использовать столько градаций в шкале, чтобы ее ошибка была меньше 0,5 балла.
Если ошибка меньше 0,5 балла, то в последовательных опросах ответы в среднем будут совпадать. При 1 x 1 ≥ 0,5 балла ответы в последовательных опросах будут в среднем отличаться на 1 балл (и выше).
Существуют способы, позволяющие добиться требуемой чувствительности [19].
На основе данных двух последовательных проб определяют пороги различаемости градаций шкалы. В том случае, если обнаружено смешение градаций, применяют один из двух способов.
Первый способ. В итоговом варианте уменьшают дробность шкалы (например, из шкалы в 7 интервалов переходят на шкалу в 3 интервала).
Второй способ. Для предъявления респонденту сохраняют прежнюю дробность шкалы и только при обработке укрупняют соответствующие ее пункты.
Второй способ кажется предпочтительнее, поскольку, как правило, большая дробность шкалы побуждает респондента и к более активной реакции. При обработке данных информацию следует перекодировать в соответствии с проведенным анализом различительной способности исходной шкалы.
Итак, предложенные способы анализа целесообразны при отработке окончательного варианта методики. Анализ устойчивости отдельных вопросов шкалы позволяет: а) выявить плохо сформулированные вопросы, их неадекватное понимание разными респондентами; б) уточнить интерпретацию шкалы, предложенной для оценки того или иного явления, и выявить более оптимальный вариант дробности значений шкалы.
Изучение устойчивости окончательного варианта методики даст представление о надежности данных (связанной с устойчивостью), которые будут получены в основном исследовании.
Обоснованность измерения. Проверка обоснованности шкалы предпринимается лишь после того, как установлены достаточные правильность и устойчивость измерения исходных данных. Как уже отмечалось, проверка обоснованности — достаточно сложный процесс и, как правило, не до конца разрешимый. И поэтому нецелесообразно сначала применять трудоемкую технику для выявления обоснованности, а после этого убеждаться в неприемлемости данных вследствие их низкой устойчивости.
Обоснованность данных измерения — это доказательство соответствия между тем, что измерено, и тем, что должно было быть измерено. Некоторые исследователи предпочитают исходить из так называемой наличной обоснованности, т. е. обоснованности в понятиях использованной процедуры. Например, считают, что удовлетворенность товаром — это то свойство, которое содержится в ответах на вопрос: «Удовлетворены ли вы товаром?». В серьезном маркетинговом исследовании такой сугубо эмпирический подход может оказаться неприемлемым.
Остановимся на возможных формальных подходах к выяснению уровня обоснованности методики. Их можно разделить на три группы: 1) конструирование типологии в соответствии с целями исследования на базе нескольких признаков; 2) использование параллельных данных; 3) судейские процедуры.
Первый вариант нельзя считать полностью формальным методом — это всего лишь некоторая схематизация логических рассуждений, начало процедуры обоснования, которая может быть на этом и закончена, а может быть подкреплена более мощными средствами.
Второй вариант требует использования по крайней мере двух источников для выявления одного и того же свойства. Обоснованность определяется степенью согласованности соответствующих данных.
В последнем случае мы полагаемся на компетентность судей, которым предлагается определить, измеряем ли мы нужное нам свойство или что-то иное.
Конструированная типология. Один из способов — использование контрольных вопросов, которые в совокупности с основными дают большее приближение к содержанию изучаемого свойства, раскрывая различные его стороны.
Например, можно определять удовлетворенность используемой моделью автомобиля лобовым вопросом: «Устраивает ли вас ваша нынешняя модель автомобиля?» Комбинация его с двумя другими косвенными: «Хотите ли вы перейти на другую модель?» и «Рекомендуете ли вы своему другу купить данную модель автомобиля?» позволяет произвести более надежную дифференциацию респондентов. Типология по пяти упорядоченным группам от наиболее удовлетворенных автомобилем до наименее удовлетворенных проводится с помощью «логического квадрата».
Обоснованность в подобного рода типологии не доказывается каким-либо формальным критерием и опирается на логические доводы.
Единственное требование, которое может быть выдвинуто при конструировании такого рода типологии, — это положительная корреляция между составляющими ее признаками. Отсутствие положительной взаимосвязи между вопросами может свидетельствовать о том, что мы не понимаем сущности измеряемого явления.
Параллельные данные. Нередко целесообразно разработать два равноправных приема измерений заданного признака, что позволяет установить обоснованность методов относительно друг друга, т. е. повысить общую обоснованность путем сопоставления двух независимых результатов.
Классифицируем параллельные процедуры в зависимости от соотношения методов и исполнителей: а) несколько методов — один исполнитель; б) один метод — несколько исполнителей; в) несколько методов — несколько исполнителей.
Несколько методов — один исполнитель. Здесь один и тот же исполнитель использует два или более различных методов для измерения одного и того же свойства.
Рассмотрим различные способы использования этого метода и прежде всего — эквивалентные шкалы. Возможны равнозначные выборки признаков для описания измерения поведения, отношения, ценностной ориентации, т.е. какой-то установки. Эти выборки и образуют параллельные шкалы, обеспечивая параллельную надежность.
Каждую шкалу рассматриваем как способ измерения некоторого свойства и в зависимости от числа параллельных шкал имеем ряд способов измерении. В качестве исполнителя выступает респондент, дающий ответы одновременно по всем параллельным шкалам. Все ответы сортируются в зависимости от принадлежности к шкале, и таким образом получаем параллельные данные.
При обработке такого рода данных следует выяснить два момента: 1) непротиворечивость пунктов отдельной шкалы; 2) согласованность оценок по разным шкалам.
Первая проблема возникает в связи с тем, что модели ответов не представляют идеальной картины; ответы нередко противоречат друг другу. Поэтому встает вопрос, что принимать за истинное значение оценки респондента на данной шкале.
Вторая проблема непосредственно касается сопоставления параллельных данных.
Рассмотрим пример неудавшейся попытки повысить надежность измерения признака «удовлетворенность автомобилем» с помощью трех параллельных порядковых шкал. Приведем две из них:
| Шкала А | |
| 11. Данная модель мне очень нравится | |
| 1. Данная модель скорее нравится, чем не нравится | |
| 8. Трудно сказать, нравится ли мне данная модель | |
| 14. Данная модель мне скорее не нравится, чем нравится | |
| 3. Данная модель мне совершенно не нравится | |
| Шкала В | |
| 2. Данная модель - одна из лучших | |
| 13. Считаю, что данная модель не хуже многих других | |
| 5. Данная модель не хуже и не лучше других | |
| 12. Считаю, что есть много моделей, которые лучше моей | |
| 4. Моя модель автомобиля хуже, чем многие другие |
Пятнадцать суждений (в порядке, обозначенном слева, в начале каждой строки) предъявляются респонденту общим списком, и он должен выразить свое согласие или несогласие с каждым из них. Каждому суждению присваивается оценка, соответствующая его рангу в указанной пятибалльной шкале (справа). (Например, согласие с суждением 4 дает оценку «1», согласие с суждением 11 — оценку «5» и т. д.)
Рассматриваемый здесь способ предъявления суждений списком дает возможность проанализировать пункты шкалы на непротиворечивость. При использовании упорядоченных шкал наименований обычно считается, что пункты, образующие шкалу, взаимно исключают друг друга и респондент легко найдет тот из них, который ему подходит.
Изучение распределений ответов показывает, что респонденты выражают согласие с противоречивыми (с точки зрения исходной гипотезы) суждениями. Например, по шкале «В» 42 человека из 100 одновременно согласились с суждениями 13 и 12, т. е. с двумя противоположными суждениями.
Наличие в ответе противоречивых суждений приводит к необходимости вычислять ошибку противоречивости. Это будет разница в рангах, наиболее противоположных для данной шкалы суждений в ответе респондента.
Итак, средние ошибки, характеризующие противоречивость для рассматриваемых шкал, оказались равными
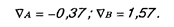
Ошибка в 1,57 балла при пятибалльной оценке, видимо, слишком велика, чтобы считать шкалу приемлемой.
Данный подход повышения надежности шкалы является весьма сложным. Поэтому его можно рекомендовать лишь при разработке ответственных тестов или методик, предназначенных для массового употребления или панельных исследований.
Один метод — несколько исполнителей. Если метод надежен, то разные исполнители дадут совпадающую информацию, но если их результаты плохо согласуются, то либо измерения ненадежны, либо результаты отдельных исполнителей нельзя считать равноценными. В последнем случае надо установить, нельзя ли рассматривать какую-либо группу результатов заслуживающей большего доверия. Решение этой задачи тем более важно, если предполагается, что одинаково допустимо получение информации любым из рассматриваемых методов (например, использование самооценок против оценок). Анализ параллельных данных с помощью описанных ниже процедур позволит установить правильность такого предположения.
Для количественных признаков при решении вопроса о согласованности оценок нескольких исполнителей предлагается выявить ошибки соответствия одним из приемов, рассмотренных при изучении устойчивости. Прежде всего, поскольку мы имеем здесь случай прямых групповых наблюдений, наиболее адекватной оценкой совпадения данных является средняя квадратическая ошибка.
Тем же способом можно изучать совпадения оценок и самооценок. Если согласованность оценок со стороны «судей» и соответствующих самооценок респондентов будет достаточно высокой, это может означать, что методика достаточно обоснована. Во всяком случае, одновременное использование оценок и самооценок дает возможность глубже понять сущность измеряемых признаков, уточнить их смысл.
Несколько методов — несколько исполнителей. Одним из способов установления обоснованности измерения некоторого качества у одного и того же респондента (объекта) является фиксирование данного свойства разными исполнителями, владеющими разными методами. Как и в предыдущих случаях, здесь нельзя установить некую абсолютную обоснованность, поэтому рассматривается лишь обоснованность одного способа относительно другого.
Использование параллельных методов измерения одного и того же свойства сталкивается с целым рядом трудностей.
Во-первых, неясно, в какой мере оба метода измеряют одно и то же качество объекта, причем, как правило, формальных критериев для проверки такой гипотезы не существует. Следовательно, необходимо прибегнуть к содержательному (логико-теоретическому) обоснованию того или иного метода.
Во-вторых, если обнаруживается, что параллельные процедуры измеряют общее свойство (данные существенно не различаются), остается вопрос о теоретико-содержательном соответствии этих процедур.
Нельзя не признать, что сам принцип использования параллельных процедур оказывается не формальным, а скорее содержательным принципом и решение остается за теоретико-методологической концепцией исследования.
Метод судейства при обосновании процедур измерения. Один из широко распространенных подходов к установлению обоснованности — это использование так называемых судей, экспертов. Исследователи обращаются к определенной группе людей с просьбой выступить в качестве компетентных лиц. Им предлагают набор признаков, предназначенный для измерения изучаемого явления, и просят оценить правильность отнесения каждого из признаков к этому объекту. Совместная обработка мнений судей позволит присвоить признакам веса или, что то же самое, шкальные оценки в измерении изучаемого явления. В качестве набора признаков могут выступить список отдельных суждений, характеристики явления и т. д.
Процедуры судейства многообразны. В основе их могут лежать методы парных сравнений, ранжирования, последовательных интервалов и т.д.
Вопрос о том, кого следует считать судьями, достаточно дискуссионен. Судьи, выбираемые в качестве представителей изучаемой совокупности, так или иначе должны представлять ее микромодель: по оценкам судей исследователь определяет, насколько адекватно будут истолкованы респондентами те или иные пункты опросной процедуры или другие, обращенные к респонденту, стимулы.
Однако при отборе судей возникает трудноразрешимый вопрос, каково влияние собственных установок судей на их оценки, ведь эти установки могут существенно отличаться от установок обследуемых в отношении того же самого объекта.
Ясно, что в каждом конкретном случае следует осуществлять контроль такого рода ошибок применительно к данной выборке судей. Так, используя мужчин и женщин в качестве судей для оценки различных занятий на досуге, нашли, что установки мужчин существенно отличаются от установок судей-женщин. Более того, оценка зависит от того, увлекается ли сам судящий данным видом досуга.
В общем виде решение проблемы состоит в том, чтобы: а) внимательно проанализировать состав судей с точки зрения адекватности их жизненного опыта и признаков социального статуса соответствующим показателям обследуемой генеральной совокупности; б) выявить эффект индивидуальных отклонений в оценках судей относительно общего распределения оценок. Наконец, следует оценить не только качество, но и объем выборочной совокупности судей.
С одной стороны, это количество определяется согласованностью: если согласованность мнений судей достаточно высока и, соответственно, ошибка измерения мала, численность судей может быть небольшой. Нужно задать значение допустимой ошибки и на основании ее рассчитать требуемый объем выборки.
При обнаружении полной неопределенности объекта, т. е. в случае, когда мнения судей распределятся равномерно по всем категориям оценки, никакое увеличение объема выборки судей не спасет ситуацию и не выведет объект из состояния неопределенности.
Здесь возникает проблема точности (устойчивости) измерения. Рассмотрим с этой точки зрения принципиально разные варианты судейства:
1) производится классификация состояний объекта (сам объект имеет качественные градации);
2) находится количественная оценка изменяющихся состояний объекта, представляющих собой континуум.
В первом случае при определении объема выборки судей необходимо задать некоторый уровень определенности в их мнениях, т. е. разброс распределения оценок должен быть не выше некоторого порогового значения. Во втором — задается уровень допустимой ошибки. Далее возникает вопрос о численности градаций в судейских оценках, что относится к чувствительности любой измерительной процедуры. В общем случае речь идет не о чем ином, как о чувствительности измерения, зависящего и от изменчивости объекта, и от устойчивости инструмента измерения. Основной способ определения дробности судейских оценок — выявление их устойчивости путем двух последовательных (с временным интервалом) судейств по единой процедуре. Эта операция уже рассматривалась выше в разделе об устойчивости.
Если объект достаточно неопределенен, то большое число градаций только внесет дополнительные помехи в работу судей и не принесет более точной информации. Нужно выявить устойчивость судейских мнений с помощью повторной пробы и, соответственно, сузить число градаций.
Выбор того или иного конкретного способа, метода или техники проверки на обоснованность зависит от многих обстоятельств.
Прежде всего следует четко установить, возможны ли какие-то существенные отклонения от запланированного предмета измерения. Если программа исследования ставит жесткие рамки, следует использовать не один, а несколько приемов проверки данных на обоснованность, с тем чтобы четко определить границы достоверности заключения по гипотезе.
Во-вторых, нужно иметь в виду, что уровни устойчивости и обоснованности данных тесно взаимосвязаны. Неустойчивая информация уже в силу недостаточной надежности по этому критерию не требует слишком строгой проверки на обоснованность. Следует обеспечить достаточную устойчивость и уже затем принять соответствующие меры для уточнения границ интерпретации данных (т. е. выявить уровень обоснованности).
Выбор конкретной техники проверки данных на обоснованность — задача скорее содержательная, чем формальная.
Многочисленные эксперименты по выявлению уровня надежности позволяют заключить, что в процессе отработки инструментов измерений со стороны их надежности целесообразна следующая последовательность основных этапов работы:
а) Предварительный контроль обоснованности методов измерения первичных данных на стадии проб методики. Здесь проверяется, насколько информация отвечает своему назначению по существу и каковы пределы последующей интерпретации данных. Для этой цели достаточны небольшие выборки в 10—20 наблюдений с последующей корректировкой структуры методики.
б) Второй этап — пилотаж методики и тщательная проверка устойчивости исходных данных, в особенности итоговых показателей индексов, многомерных шкал и т. п. На этом этапе нужна выборка не менее 100 человек, представляющая микромодель реальной совокупности обследуемых с учетом представительства по существенным характеристикам объекта исследования.
в) В период этого же общего пилотажа осуществляются все необходимые операции, относящиеся к проверке уровня обоснованности. Результаты анализа данных генерального пилотажа приводят к усовершенствованию методики, к доработке всех ее деталей и в итоге — к получению окончательного варианта методики для основного исследования.
г) В начале основного исследования желательно провести проверку используемого варианта методики на устойчивость, с тем чтобы рассчитать точные показатели ее устойчивости. Последующее уточнение границ обоснованности проходит через весь анализ результатов самого исследования.
Вне зависимости от использованного метода оценки надежности у исследователя имеется четыре последовательных шага по повышению надежности результатов измерений.
Во-первых, в случае чрезвычайно низкой надежности измерений некоторые вопросы просто выбрасываются из анкеты, особенно когда степень надежности можно определить в процессе разработки анкеты.
Во-вторых, исследователь может «свернуть» шкалы и использовать меньше градаций. Скажем, шкала Лайкерта в этом случае может включать только следующие градации: «согласен», «не согласен», «не имею мнения». Обычно так поступают, когда пройден первый шаг и обследование уже было проведено.
В-третьих, как альтернатива второму варианту оценка надежности проводится на индивидуальной основе, т.е. осуществляется оценка надежности ответов отдельных экспертов (особенно если использовался метод повторного тестирования) двух групп.
Ответы ненадежных респондентов просто не учитываются при проведении заключительного анализа. Данный подход может рассматриваться и как дополнение ко второму шагу.
Наконец, после того как первые три шага были проведены,можнооценить уровень надежности измерений. Обычно надежность измерений характеризуется коэффициентом, изменяющимся от нуля до единицы, где единица характеризует максимальную надежность.
Обычно считается, что минимально приемлемый уровень надежности характеризуют цифры 0,65—0,70, особенно если измерения проводились впервые.
Очевидно, что в процессе проведения разными фирмами разнообразных и многочисленных маркетинговых исследований имела место последовательная адаптация шкал измерений и методик их проведения к целям и задачам конкретных маркетинговых исследований. Это облегчает решение задач, рассмотренных в данном разделе, и делает их применение скорее необходимым при проведении оригинальных маркетинговых исследований.
Достоверность измерений характеризует совершенно другие аспекты, чем надежность измерений. Измерение может быть надежным, но не достоверным. Последнее характеризует точность измерений по отношению к тому, что существует в реальности. Например, респонденту задали вопрос о его годовом доходе, который составляет менее 25 000 долларов. Не желая называть интервьюеру истинную цифру, респондент указал доход «более 100 000 долларов». При повторном тестировании он снова назвал данную цифру, демонстрируя высокий уровень надежности измерений. Ложь не является единственной причиной низкого уровня достоверности измерений. Можно также назвать плохую память, плохое знание респондентом действительности и т.п.
Главное направление проверки достоверности измерений заключается в получении информации из различных источников. Это может быть осуществлено различными методами, среди которых прежде всего следует отметить следующее.
Надо стремиться составлять вопросы таким образом, чтобы их формулировки способствовали получению достоверных ответов. Далее, в анкету могут включаться вопросы, связанные друг с другом.
Например, в анкету помещается вопрос о том, в какой степени респонденту нравится какой-то продукт питания определенной марки. И далее спрашивается, какое количество данного товара было куплено респондентом за последний месяц. Второй вопрос направлен на проверку достоверности ответа на первый вопрос.
Часто для оценки достоверности измерений используется два различных метода или источников получения информации. Например, после письменного заполнения анкет ряду респондентов из первоначальной выборки дополнительно задаются те же вопросы по телефону. По схожести ответов судят о степени их достоверности.
Иногда образуют на основе одних и тех же требований две выборки респондентов и для оценки степени достоверности сравнивают их ответы.
Дата добавления: 2015-03-19; просмотров: 806;
