Теоретическое введение. Жидкости сопротивляются изменению их объема, но не сопротивляются изменению формы

Жидкости сопротивляются изменению их объема, но не сопротивляются изменению формы. С этим свойством связан характерный для жидкостей закон Паскаля: передаваемое жидкостью во все стороны давление одинаково.

Твердые же тела сопротивляются как изменению объема, так и изменению формы; они сопротивляются, как говорят, любому деформированию. Для твердых тел не справедлив закон Паскаля. Передаваемое твердым телом давление различно в разных направлениях. Давления, возникающие в твердом теле при его деформировании, называются напряжениями. В отличие от давления в жидкости, упругие напряжения в твердом теле могут иметь любые направления по отношению к площадке, на которую действуют силы. Но при всем разнообразии деформации твердых тел оказывается возможным любую деформацию тела свести к двум основным типам, которые поэтому называют элементарными деформациями. Ими являются растяжение (сжатие) и сдвиг. Любые другие типы деформаций (изгиб, кручение, …) можно представить как комбинацию деформаций растяжения и сдвига.

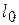В данной работе изучаются величины, характеризующие упругую деформацию растяжения. Пусть на цилиндр первоначальной длины и диаметра 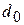действует растягивающая сила 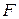(рис. 14.1). При этом образец увеличивает свою длину на 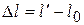, 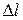– абсолютное удлинение. Величину

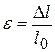(14.1)

называют относительным удлинением (относительной деформацией). При растяжении 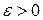, при сжатии 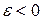. При однородном растяжении величина 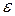во всех точках тела одинакова.

Отношение силы 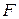к величине сечения 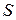, на которое она действует, называется механическим напряжением 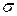в данном сечении:

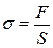. (14.2)

Опыт показывает, что при малых деформациях, при малых относительных удлинениях 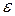для цилиндров разного сечения 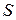и длины 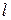, но сделанных из одного и того же материала, выполняется закон Гука: напряжения пропорциональны деформации:

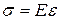, (14.3)

где 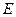– коэффициент пропорциональности, зависящий от свойств материала цилиндра, но не зависящей от его размеров. Он называется модулем упругости или модулем Юнга данного материала. Из (14.1), (14.2) и (14.3) можно получить закон Гука в школьной формулировке:

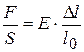, или 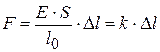; (14.4)

при этом коэффициент жёсткости 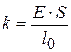зависит как от свойств материала, так и от длины и сечения образца.

Если с прекращением действия вызвавших деформацию внешних сил тело возвращается в исходное недеформированное состояние, то деформации называются упругими. Деформации будут упругими, если они достаточно малы.

Модуль Юнга, однако, еще не характеризует полностью упругие свойства тела. Это видно и из рисунка 14.1: продольное растяжение цилиндра связано с сокращением его поперечных размеров: удлиняясь, цилиндр одновременно становится более тонким. Характеристикой этого изменения является относительное поперечное сжатие

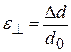(14.5)

где 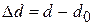– абсолютное поперечное сжатие. При растяжении 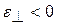, при сжатии .

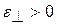Очевидно, что величина 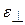также пропорциональна растягивающему напряжению 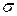, и тем самым она пропорциональна и величине относительного удлинения 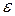. Вводится соотношение, называемое коэффициентом Пуассона:

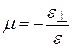. (14.6)

Коэффициент Пуассона 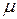, как и модуль Юнга 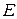, не зависит от размеров тела и является константой, характеризующей свойства вещества. Можно показать из общих требований механической устойчивости твердого тела, что значение коэффициента Пуассона меняется в пределах от 0 до 0.5. Значение 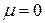достигается у пористых тел (например, у пробки), не меняющих при растяжении своих поперечных размеров. Близкие к 0.5 значения 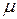достигаются у таких тел, как резина, которые значительно легче поддаются изменению своей формы, чем изменению своего объема.

Таким образом, упругие свойства твердого тела характеризуются двумя величинам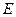и: и .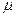

Отметим, что в наших рассуждениях мы подразумеваем, что твердое вещество изотропно – свойства его одинаковы во всех направлениях. Упругие свойства анизотропных тел – монокристаллов – характеризуются большим числом упругих постоянных (не 2, а 21 – в самом общем случае).

Упругие деформации, по определению, исчезают после снятия вызывающих их напряжений (абсолютно упругое тело). Конечно, реальные твердые тела вовсе не обладают этой способностью в полной мере. Только пока деформации тела не превосходят известных пределов, оно восстанавливает свою форму, и то лишь с известной степенью точности. Минимальное механическое напряжение, при котором реальные тела ведут себя приблизительно как тела абсолютно упругие, называется пределом упругости. Различные тела обладают различным пределом упругости, но для всех тел существует такое напряжение, что после снятия нагрузки тело уже не возвращается к исходному состоянию и сохраняет в заметной степени измененную форму. Такие деформации называются остаточными или пластическими.

Рассматривать тела как абсолютно упругие имеет смысл только при условии, что деформации тел заведомо не достигают предела упругости. При малых и медленных деформациях многие реальные твердые тела можно считать абсолютно упругими. Вопрос о том, как малы и медленны должны быть деформации, чтобы данное реальное тело можно было рассматривать как абсолютно упругое, должен быть решен на опыте путем изучения поведения тел при различных величинах деформаций.

Для этой цели применяются специальные машины, в которых образцы испытуемого материала подвергаются различным деформациям. Результаты испытаний материалов представляют в виде графиков, изображающих связь между деформациями образца и напряжениями (силами), в нем возникающими (рис.14.2). Как видно из рисунка 14.2, при малых деформациях напряжение пропорционально деформации: 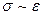(участок 0-1). Это область область пропорциональности. Максимальное напряжение, при котором выполняется закон Гука, называется пределом пропорциональности. Далее напряжения растут медленнее, чем деформации (1-3 на рис.14.2). В этой области и лежит предел упругости тела. Точного определения предела упругости дать вообще невозможно, так как малые остаточные деформации наблюдаются всегда. Пределом упругости можно считать такое наибольшее механическое напряжение, после снятия которого остаточные деформации невелики (они не превышают некоторой определенной условно выбранной доли от наибольшей деформации, которой подвергается образец, например, 0.001%). Предел упругости 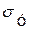лежит обычно близко за пределом пропорциональности 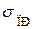. Дальше начинается область текучести участок 3-4 на рис.14.2). Под действием напряжения, равного пределу текучести 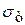, тело непрерывно увеличивает свою деформацию без увеличения нагрузки; оно будет течь как жидкость. При еще больших деформациях наступает разрушение (точка 5). Предел прочности 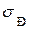– минимальное напряжение, при котором начинается разрушение тела.

Область упругих деформаций в большинстве применяемых на практике материалов очень незначительна (например, для стали пределу упругости соответствует значение 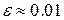). Поэтому наибольшие деформации, которые может выдержать данный материал без разрушения, определяются главным образом величиной области текучести. Материалы, для которых эта область мала, способны выдерживать без разрушения только малые деформации – это хрупкие материалы. Те же, которые способны без разрушения выдерживать большие деформации – вязкие материалы. Например, чугун и сталь имеют примерно одинаковую область упругих деформаций и примерно одинаково ведут себя в этой области – они в одинаковой степени упругие. Но область текучести у чугуна гораздо меньше, чем у стали, поэтому он гораздо более хрупок.