Надежность систем при разных способах структурного резервирования

Принципы расчета надежности систем с резервированием не отличаются от тех, что нами уже рассмотрены. Однако существуют некоторые специфические правила расчетов надежности систем с различными способами резервирования.

Расчеты систем с нагруженным резервированием без восстановления проводятся как для параллельных и последовательных соединений. При этом считается, что отказ резервной группы (основной + резервный элементы) имеет место только после отказа последнего элемента. Надежность резервных элементов до и после отказа основного элемента не меняется, так как не меняется режим их работы. Для случая равнонадежных одного основного и n -1 резервных элементов вероятность отказа, вероятность безотказной работы и средняя наработка на отказ рассчитываются по схеме параллельного соединения и при экспоненциальном законе равны:

.

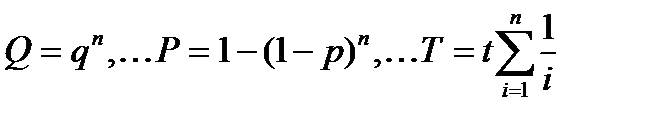При ненагруженном резервировании методом замещения отказ системы произойдет тогда, когда откажет последний элемент. Надежность резервного элемента меняется, как только он включается в работу взамен отказавшего основного или предыдущего резервного (при многократном резервировании) элементов. При включении по методу замещения в схему резервной группы, состоящей из одного основного и n -1 резервных элементов, вероятность отказа уменьшается примерно в n! раз (при q < 0,1), значительно возрастают вероятность безотказной работы и средняя наработка на отказ (экспоненциальный закон распределения):

.

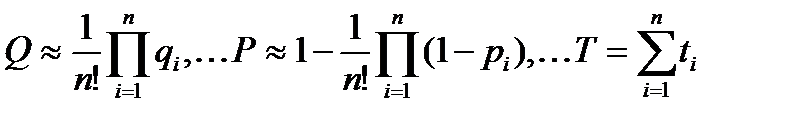Ненагруженное резервирование дает больший выигрыш в надежности, чем нагруженное. О повышении надежности при резервировании см. также ЛР 6.

Облегченное резервирование применяется в системах с большой инерционностью переходных процессов в случаях, когда горячее резервирование не обеспечивает требуемой надежности. Отказ резервной группы (основной + резервный элементы) произойдет лишь при отказе последнего элемента. Надежность резервного элемента различна в резервном и рабочем режимах. Точные формулы надежности системы с облегченным резервированием громоздки. При экспоненциальном законе распределения вероятность безотказной работы системы из равнонадежных элементов приблизительно равна:

.

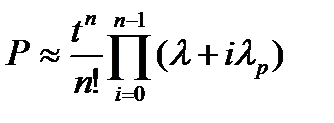Здесь λ_р – интенсивность отказов при работе элемента в резервном режиме.

ПРИМЕР 18

Показать, что ненагруженное резервирование дает больший выигрыш в увеличении средней наработки на отказ по сравнению с нагруженным резервированием (закон распределения экспоненциальный, элементы равнонадежны, резервная группа состоит из n элементов, один из них основной, остальные – резервные).

При экспоненциальном законе распределения средняя наработка на отказ системы с n -кратно резервированным элементом при горячем резервировании равна:

.

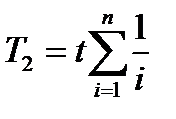То же при ненагруженном резервировании:

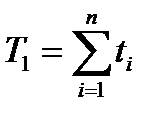
Выигрыш от ненагруженного резервирования в сравнении с нагруженным равен:

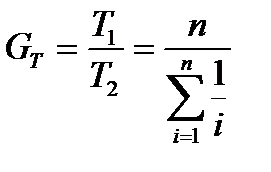. Для n = 2 G_T = 2/1,5 = 1,33, а для n = 10 G_T = 10/2,93 = 3,41.

Структурное резервирование позволяет повысить надежность систем практически до любого уровня. Однако это сопряжено со значительными затратами, существенным увеличением числа элементов и серьёзным усложнением системы. В связи с этим существует проблема оптимального уровня надежности.

Различают два основных типа задач оптимизации:

1. Прямая основная задача оптимизации – определение числа резервных элементов для обеспечения заданной надежности при минимуме расходуемых ресурсов.

2. Обратная основная задача оптимизации - определение числа резервных элементов для обеспечения максимальной надежности при заданных расходуемых ресурсах.

Под ресурсами подразумеваются все их виды: стоимость, вес, габариты, число элементов и др.

В простейших случаях задача оптимального структурного резервирования сводится к определению элемента или элементов, резервирование которых дает наибольший эффект (наибольший коэффициент выигрыша). Наличие ограничений существенно усложняет задачу оптимизации. Без привлечения сложного математического аппарата уже не обойтись. Рассмотрение математических методов оптимизации выходит за рамки нашего курса.

Особо следует рассмотреть системы с восстановлением элементов. Восстановление в системах без резервирования не изменяет вероятности безотказной работы, но повышает комплексные показатели надежности, например, коэффициент готовности. Иная ситуация в системах с резервированием. При резервировании восстановление является одним из методов повышения надежности в целом, в том числе и вероятности безотказной работы. Особенности расчета надежности резервированных систем с восстановлением обусловлены тем, что рассмотренные выше методы в данном случае практически неприменимы. Для систем с восстановлением наиболее часто применяют метод топологии и теории графов.

Анализ надежности таких систем начинается с построения графа состояний и событий (переходов) системы.

В заключение следует отметить, что структурное резервирование не является абсолютным методом повышения надежности любой системы. В системах с большими значениями наработки возможны ситуации (при больших значениях наработки), в которых резервированная система имеет меньшую вероятность безотказной работы, чем нерезервированная, т.е. оказывается менее надежной.