Классификация способов резервирования элементов систем
| № п/п | Признак | Способ резервирования | Содержание способа |
| По схеме включения резерва | Общее резервирование | Резервируется весь объект в целом | |
| Раздельное резервирование | Резервируются отдельные элементы или группы | ||
| По однородности резервирования | Однородное резервирование | Используется один способ резервирования | |
| Смешанное резервирование | Сочетаются различные виды резервирования | ||
| По способу включения резерва | Постоянное резервирование | При отказе не требуется перестройка структуры системы | |
| Динамическое резервирование | При отказе происходит перестройка структуры системы | ||
| Резервирование замещением | Функции основного элемента передаются резервному только после отказа основного элемента | ||
| Скользящее резервирование | Несколько основных элементов резервируются одним или несколькими резервными, каждый из которых может заменить основной | ||
| Фиксированное резервирование | Каждый из резервных элементов закреплён за одним из основных | ||
| По восстановлению отказавших элементов | Резервирование с восстановлением | Отказавший элемент восстанавливается без прекращения функционирования всей системы | |
| Резервирование без восстановления | Отказавший элемент не восстанавливается | ||
| По состоянию резерва | Нагруженное («горячее») резервирование | Резервный элемент находится в режиме основного элемента | |
| Облегчённое («тёплое») резервирование | Нагрузка резервного элемента ниже нагрузки основного элемента | ||
| Ненагруженное («холодное») резервирование | Резервный элемент находится в ненагруженном состоянии |
Структурное резервирование характеризуется кратностью – отношением числа резервных элементов к числу основных элементов. Резервирование с кратностью 1:1 называется дублированием.
При любом способе структурного резервирования последовательные схемы соединений элементов надежности заменяются параллельными.
Усилия по повышению надёжности оценивают коэффициентом выигрыша надёжности, равным отношению значений показателя надёжности до и после принятых мер: Gp=P1/P.
ПРИМЕР 15
Найти коэффициент выигрыша надежности системы из n=3 последовательных равнонадежных элементов при резервировании одного из них, если вероятность безотказной работы этого элемента равна 0,8 и 0,9.
Если в системе из n последовательных элементов продублировать (резервировать) один k–ый, то коэффициент выигрыша надежности будет равен:
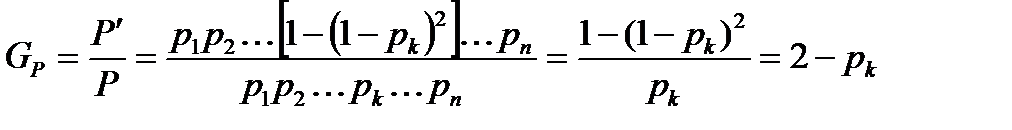= 2-0,8 = 1,2 и 2-0,9 = 1,1.
Эффект от резервирования любого элемента системы можно предсказать по значению производной по этому элементу вероятности безотказной работы. Рассмотрим это на примере простой системы (рис. 19).
ПРИМЕР 16
| Рис.19. Пример системы для резервирования |
Функция работоспособности системы имеет вид: А=а1а3+а2а3=А1+А2. По теореме умножения вероятностей Р(А1)=Р(а1а3)=р1р3, Р(А2)=Р(а2а3)=р2р3. По теореме сложения вероятностей Р(А)=Р(А1+А2)=1-(1-р1р3)(1-р2р3)=р1р3+р2р3-р1р2р3 (с учетом того, что одно и то же событие не может произойти одновременно дважды, т.е. сомножитель р32 не имеет смысла).
Производные вероятности безотказной работы системы по элементам равны:
Р1(р1)=р3-р2р3=(при р1=р2=р3)=р-р2.
Р1(р2)=р3-р1р3=(при р1=р2=р3)=р-р2.
Р1(р1)= Р1(р2).
Р1(р3)=р1+р2-р1р2=(при р1=р2=р3)=2р-р2.
Тогда разница Р1(р3) - Р1(р1)=р всегда больше нуля. Таким образом, выгоднее всего резервировать элемент под номером 3.
В заключение следует отметить, что в рассматриваемых здесь и далее примерах резервирования не учитывается надежность переключателей - элементов, обеспечивающих подключение резервных элементов при отказах основных элементов. Другими словами, предполагается, что переключатели абсолютно надежны. На практике надежность переключателей должна учитываться, но для получения основных зависимостей и качественных выводов это не так важно, тем более что включение в расчеты надежности переключателей существенно их усложняет.
Применяются два метода резервирования последовательно соединенных элементов: общее и раздельное (рис. 20).
| n |
| n |
| 11 |
| 21 |
| n1 |
| 11 |
| 21 |
| n1 |
| a) |
| б) |
| Рис. 20. Нагруженное резервирование: а) – общее, б) - раздельное |
Выигрыш в надежности по вероятности безотказной работы при общем резервировании равен:
Gp=Pp/P=(при P=pn и Pp=1-(1-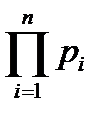 
)2=р(2-р))=р(2-р)/р=2-р,
а при раздельном:
Gp=Pp/P=(при P=pn и Pp=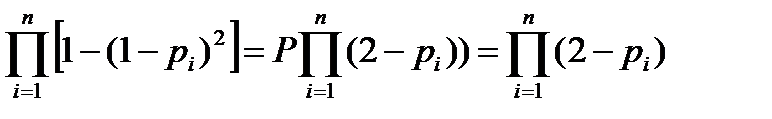 
=(2-p)n.
Раздельное резервирование эффективнее!
ПРИМЕР 17
Определить эффективность резервирования элемента №3 на схеме по рис. 19 при равнонадежных элементах и вероятности их безотказной работы р=0,8.
При равнонадежных элементах, вероятность безотказной работы основной системы равна: Р(А)=р2(2-р).
При резервировании элемента №3 элементом №4 схема преобразуется в следующий вид:
| Система после резервирования |
Функция работоспособности преобразованной системы имеет вид:
А=а2а3+а2а4+а1а3+а1а4.
Вероятности безотказной работы при событиях А1...А4:
Р(А1)=Р(а2а3)=р2р3.
Р(А2)=Р(а2а4)=р2р4.
Р(А3)=Р(а1а3)=р1р3.
Р(А4)=Р(а1а4)=р1р4.
Тогда по теореме сложения вероятностей вероятность безотказной работы системы с резервированием:
Рр(А)=Р(А1+А2+А3+А4)=1-(1-р2р3)(1-р2р4)(1-р1р3)(1-р1р4).
Если мы произведем перемножения с учетом невозможности одновременной реализации одного и того же события, то при равнонадежных элементах получим:
Рр(А)=4р2-4р3+р4=р2(2-р)2.
Найдем Рр(А) иным способом. Система состоит из двух последовательных элементов, образуемых параллельным включением элементов 1-2 и 3-4. Тогда q12=q1q2, q34=q3q4 и P12=1-q1q2=1-(1-p1)(1-p2)= (при равнонадежных элементах)=1-(1-p)2=p(2-p); P34=1-(1-p3)(1-p4)=1-(1-p)2=p(2-p). Тогда Р(А)=Р(А1)Р(А2)=р2(2-р)2. Получен тот же результат!
Коэффициент выигрыша надежности при резервировании элемента №3 равен:
Gp=Pp/P=2-p=(p=0,8)=1,2.
Дата добавления: 2015-03-19; просмотров: 2008;