Динамическая модель

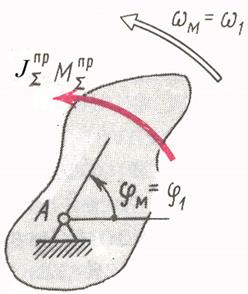Положение механизма с W=1 вполне определяется одной координатой, которая называется обобщенной координатой. В качестве обобщенной координаты чаще всего принимают угловую координату звена, совершающего вращательное движение. В этом случае динамическая модель будет представлена в виде:

- обобщенная угловая координата модели

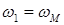- угловая скорость модели

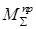- суммарный приведенный момент (обобщенная сила - эквивалент всей заданной нагрузки, приложенной к механизму)

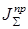- суммарный приведенный момент инерции, являющийся эквивалентом инерционности механизма.

В случае приведения, фактически действующие силы и моменты заменяем суммарным приведенным моментом, приложенным к динамической модели.

Следует подчеркнуть, что сделанная замена не должна нарушить закона движения механизма, определяемого действием фактически приложенных сил и моментов.

В основу приведения сил и моментов должно быть положено условие равенства элементарных работ, т.е. элементарная работа каждой силы на возможном перемещении точки ее приложения или момента на возможном угловом перемещении того звена, на котором он действует должна быть равна элементарной работе приведенного момента на возможном угловом перемещении динамической модели.

Рассмотрим в качестве примера приведение сил и моментов, приложенных к звеньям машинного агрегата (рис. 6.6) , назначив в качестве обобщенной координаты угловую координату .

Определим 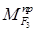, заменяющий приложенную силу 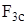. По условию равенства элементарных работ

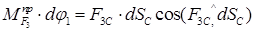
решив относительно искомой величины 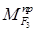и разделив возможные перемещения на время, получим

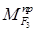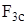
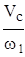= cos( 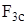, 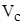), где cos(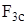 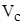)= 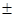1

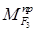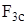
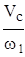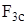
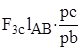= = = , где 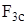для решения на ЭВМ,

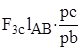с использованием 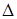скоростей.

Аналогично произведем приведение к динамической модели (звену 1) сил 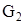, , 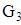и .

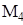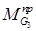= cos( 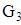, 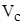) = 0 ,0 т.к. cos( 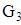, 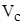) = 0.

=

= =

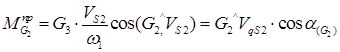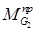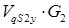
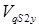- проекция скорости центра масс 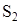на ось у.

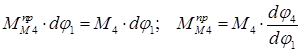
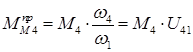
Подобным же образом найдем .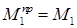

Если алгебраически сложить все приведенные моменты, приложенные к начальному звену, то получим суммарный приведенный момент, который заменяет собой все силы и моменты, действующие на механизм.

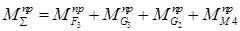(6.5)