Устранение ошибки наиболее целесообразно не путем набора нового правильного выражения, а редактированием ошибочного.

Существует несколько способов возврата в строку ввода ранее введенных команд.

Первый способ – с помощью клавиш <↑> и <↓> (см. разд. 2).

При вычислении значения обнаружена синтаксическая ошибка: не определена функция sqr. Клавишей <↑> вернем команду >> sqr(2) в командную строку. Отредактируем ее: после sqr вставим t и нажмем клавишу <Enter>:

>> sqrt(2)

ans =

1.4142

Второй способ – копирование из окна Command History.

Для активизации окна Command Historyнеобходимо войти в меню Viewкомандного окна, выбрать вкладку с одноименным названием и щелкнуть на ней левой кнопкой мыши (поставить галочку). В этом окне отображаются дата и время каждого сеанса работы в MATLAB, а также перечень команд, вводимых в течение каждого сеанса (рис. 4).

Если в окне Command History дважды щелкнуть левой кнопкой мыши на какой - либо команде, эта команда будет выполнена. Это равнозначно вводу данной команды в командное окно и последующему нажатию клавиши <Enter> (рис. 4).

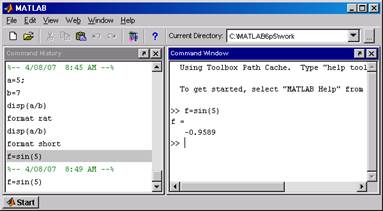
Рис. 4

Если щелкнуть на какой - либо команде окна Command Historyлевой кнопкой мыши, то данная команда становится текущей (на синем фоне). Можно выделить нужную последовательность команд при помощи комбинации клавиш <Shift>+<↑>, <Shift>+<↓>. При щелчке правой кнопкой мыши на выделенной области окна Command Historyпоявляется всплывающее меню. Выбор пункта Copy приводит к копированию выделенной последовательности в буфер обмена Windows. При щелчке правой кнопкой мыши на области окна Command Window появляется всплывающее меню. Выбор пункта Paste приводит к вставке скопированной последовательности команд в командную строку. Весь вставленный в командную строку набор команд отправляется на выполнение нажатием клавиши <Enter>.

До нажатия клавиши <Enter> содержимое набора можно редактировать, используя обычные приемы редактирования, общие для Windows - приложений, в том числе и с помощью мыши. Можно вносить в команды необходимые изменения, удалять лишние команды и добавлять новые. При редактировании клавиши <↑>и<↓> могут использоваться для перемещения между строками набора.

Третий способ – копирование из содержимого текстового поля рабочего окна.

В текстовом поле можно выделить с помощью мыши любую команду и копировать ее в буфер обмена операционной системы Windows, а затем вставить в командную строку. Выделение и вставка производится теми же средствами, что и в других Windows - приложениях.

При вычислениях любое арифметическое выражение набирается с клавиатуры в командной строке. Редактор MATLAB укажет на синтаксические ошибки. Но он не обнаружит так называемые семантические (смысловые) ошибки, когда, например, пользователь ошибочно заменит знак операции <+> на <–> или неверной расстановкой скобок изменит общий порядок выполнения операций и т. д.

MATLAB совместно с пакетом ToolBox Symbolic Math предоставляет возможность визуального контроля введенного выражения.

Пусть требуется вычислить значение выражения

F =

при x = 0,1, y = 0,2.

Введем значения переменных x и y. Наберем с клавиатуры арифметическое выражение F и вычислим его значение, нажав клавишу <Enter>. Редактор MATLAB синтаксических ошибок ввода не обнаружил. В результате получим F = 7,2111 (рис. 5).

В третьей командной строке редактируется предыдущая команда (<↑>) для придания арифметическому выражению F статуса символьного с помощью команды sym. Выведенное в командное окно символьное выражение F синтаксически совпадает с арифметическим.

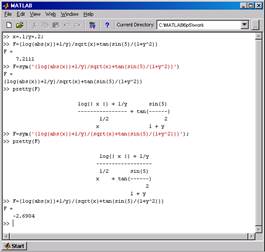
Рис. 5

Далее команда pretty(F)выводит в командное окно символьное выражение F в виде, близком к математической формуле. Выведенная и исходная формулы не совпадают. Предполагаемая ошибка ввода – знаменатель исходной дроби не заключен в скобки.

В пятой командной строке редактируется третья команда (<↑↑>) для устранения ошибки ввода.

Затем команда pretty(F) отображает в командном окне исправленное выражение. Теперь выведенная формула совпадает с исходной.

В седьмой командной строке редактируется пятая команда (<↑↑>) для придания исправленному символьному выражению статуса арифметического. Седьмая команда вычисляет правильный результат F = - 2,6904.

Иногда появляется совершенно неожиданный или явно неправильный результат. Так, если вы попытаетесь вычислить при x = -8, набирая

>> x=-8;r=x^(1/3)

r =

1.0000 + 1.7321i

ответ, который система MATLAB создает, не похож на ожидаемый результат -2. Тем не менее, полученный результат является кубическим корнем из -8, что подтверждается возведением этого результата в куб:

>> r^3

ans =

-8.0000 + 0.0000i

Дело в том, что многозначная функция имеет в комплексной плоскости три ветви, а уравнение x³ = -8 – три разных значения корня:

>> solve('x^3=-8')

ans =

[ -2]

[ 1-i*3^(1/2)]

[ 1+i*3^(1/2)]

Система MATLAB воспринимает для отрицательного x как значение

.

Поэтому для получения ожидаемого результата при вычислении , x = -8, надо набирать

>> x=-8;r=sign(x)*abs(x)^(1/3)

r =

-2

Это обстоятельство надо обязательно учитывать, например, при построении графика функции y = .