ОСНОВНЫЕ СВЕДЕНИЯ О ЗУБЧАТЫХ КОЛЕСАХ
[1] Традиции стаи – это совокупная информация стаи, передающаяся негенетическим путем, охватывает практически все стороны жизни стаи: способы охоты, обитание на конкретной территории, особенности взаимоотношений и т.д. (по Л.В. Крушинскому).
[2] У собак граница демонстрации силы и собственно силового приема проходит не там, где у людей. Лояльные союзники не пускают в ход зубы, они пользуются ритуальными толчками, что вполне соответствует увесистому шлепку рукой.
[3] Корытин С.А., Бибиков Д.И. Волк. М., 1985. С. 311–324.
[4] В скобках указаны фамилии ученых, которым принадлежит данное определение.
ОСНОВНЫЕ СВЕДЕНИЯ О ЗУБЧАТЫХ КОЛЕСАХ
Зубчатые зацепления широко распространены в технике. Они служат для передачи вращательного момента от одного вала к другому. Оси вращения валов могут располагаться параллельно друг другу, а также пересекаться или скрещиваться между собой. Если зубчатые передачи состоят из двух колес, то колесо, которое передает момент другому колесу, называется ведущим, а второе называется ведомым. В зависимости от соотношения числа зубьев ведущего и ведомого колес изменяется частота вращения вала ведомого колеса.
Кроме того, зубчатые колеса могут применяться для преобразования вращательного движения в поступательное. В этом случае зубчатая передача называется реечной и состоит из зубчатого колеса и рейки.
В зубчатых передачах усилие от одного колеса к другому передается посредством зубьев, последовательно вступающих в контакт друг с другом. В зависимости от функционального назначения и условий работы зубья могут иметь различную форму и расположение относительно оси колеса.
На рис. 1 показаны зубчатые зацепления с различной формой зубьев:
а) цилиндрическая передача с прямыми зубъями;
б) цилиндрическая передача с косыми зубьями;
в) цилиндрическая передача с шевронными зубьями;
г) коническая передача с прямыми зубьями.
В зависимости от формы профиля зуба передачи подразделяются на эвольвентные, неэвольвентные (передачи Новикова) и циклоидальные.
На рис. 2 показано зубчатое колесо с эвольвентным профилем зуба.
Основными параметрами зубчатого колеса являются: диаметр делительной окружности d, модуль m и число зубьев z.
Диаметр делительной окружности d равен диаметру цилиндрической поверхности, которая делит зубья на головку и ножку. Окружной шаг зацепления зубьев Pt (рис. 2) представляет собой расстояние между одноименными точками профиля соседних зубьев по дуге делительной окружности.
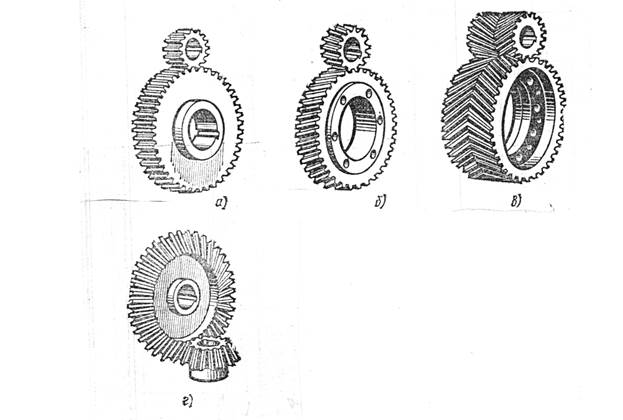
Рис. 1. Зубчатые зацепления
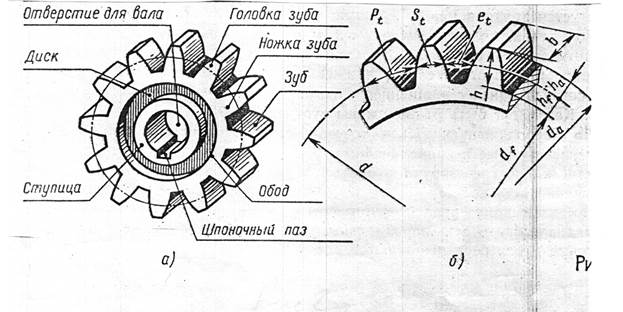
Рис. 2. Зубчатое колесо с эвольвентным профилем зуба
Величина Ptделится поверхностями соседних зубьев на две равные части окружную толщину зуба St и окружную ширину впадиныℓt (рис. 2).
Длина делительной окружности, таким образом, равна произведению окружного шага зацепления на число зубьев
πd= Pt·z (1)
Модулем зубчатого колеса называется отношение окружного шага зацепления Ptк величине p
m= 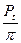 (2)
(2)
На основании уравнений (1) и (2) можно сделать вывод, что
d= mz (3)
Величина модуля определяет размер зуба и рассчитывается в зависимости от момента вращения, передаваемого зубчатым колесом. Модуль является величиной стандартной и поэтому после расчета зуба на прочность конструктор выбирает величину модуля из таблицы в соответствии с ГОСТ 9563-60, ближайшую к расчетной.
Для эвольвентных цилиндрических зубчатых колес общего назначения высоту головки зуба ha и величину ножки зуба hfопределяют по формулам
ha=m, (4)
hf=1,25m. (5)
Таким образом, высота зуба
h=2,25m.(6)
На основании уравнений (3) - (5) можно определить диаметр окружности впадин dfи диаметр окружности выступовda
df=m(z - 2,5) (7)
da=m(z + 2)(8)
Дата добавления: 2015-03-14; просмотров: 929;
