Методы нахождения вероятности безотказной работы
В общем случае безотказная работа определяется условием непревышения действующего диагностического показателя 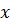 своих допустимых значений
своих допустимых значений 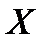 , следующих из свойств технической системы:
, следующих из свойств технической системы:
 , (2.1)
, (2.1)
где 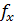 и
и 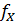 - плотности вероятности распределений величин F(x) и F(X).
- плотности вероятности распределений величин F(x) и F(X).
Для различных сочетаний законов F(x) и F(X) имеются готовые решения для (1), которыми пользуются при вычислении ВБР.
В инженерной практике механических систем получил распространение метод, при котором ВБР оценивается по площади перекрытия графиков плотностей распределения f(X) и f(x) ( 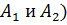 (штриховка, рис.2.1) [7]:
(штриховка, рис.2.1) [7]:
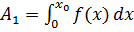 ,
,  (2.2)
(2.2)
Тогда ВБР определяется неравенством:
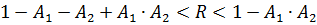 (2.3)
(2.3)
Данный метод удобен, поскольку позволяет с минимальным риском установить предельную при диагностике величину 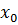 . Также для инженерных задач удобен метод нахождения ВБР из графиков F(x) и F(X), тогда значение R устанавливается из условия
. Также для инженерных задач удобен метод нахождения ВБР из графиков F(x) и F(X), тогда значение R устанавливается из условия 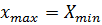 (рис. 2.2). Этот метод целесообразно применять при недостаточном объёме эмпирических данных, а также когда выборка формируется, например, методом Монте-Карло и закон её распределения произвольный. Поскольку практический интерес представляет правая ветвь графика f(x) и правая ветвь графика f(X), то для оценки ВБР используют асимптотические распределения максимальных значений х и минимальных значений X.
(рис. 2.2). Этот метод целесообразно применять при недостаточном объёме эмпирических данных, а также когда выборка формируется, например, методом Монте-Карло и закон её распределения произвольный. Поскольку практический интерес представляет правая ветвь графика f(x) и правая ветвь графика f(X), то для оценки ВБР используют асимптотические распределения максимальных значений х и минимальных значений X.
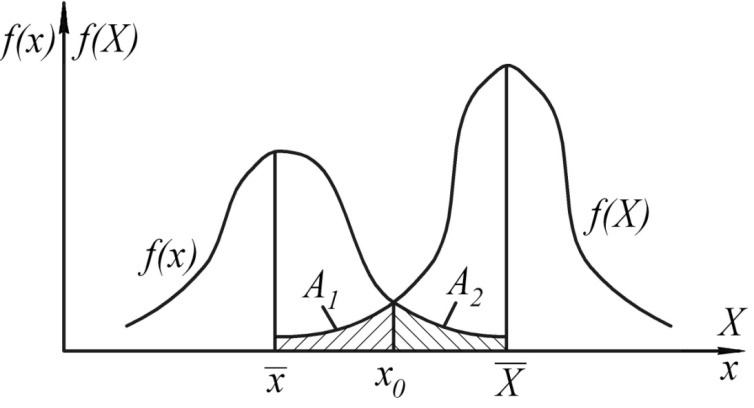
Рис. 2.1. Плотность вероятности распределения величин 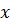 и
и 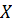
Рассмотренные методы пригодны лишь для отказов внезапного (однократного) типа и не годятся для отказов постепенного типа, что хорошо понимают специалисты по общей теории надёжности. Несмотря на это, представители вероятностно-физического направления надёжности пытаются адаптировать данные методы поиска ВБР для кумулятивных процессов, например, усталостного разрушения. В подобном случае неясно, что же принимать за величину 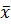 . Очевидно, что медианное значение спектра напряжений для этого не подходит. Разработчики методов расчёта деталей машин на ограниченную долговечность считают, что отказ связан с вариациями предела выносливости
. Очевидно, что медианное значение спектра напряжений для этого не подходит. Разработчики методов расчёта деталей машин на ограниченную долговечность считают, что отказ связан с вариациями предела выносливости 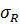 (в качестве свойства механической системы X) и только максимальных (а не всех действующих, как в спектре) напряжений блока
(в качестве свойства механической системы X) и только максимальных (а не всех действующих, как в спектре) напряжений блока  [8]. Тогда в качестве значений
[8]. Тогда в качестве значений 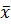 следует принимать медианное значение
следует принимать медианное значение  , что носит условный характер. Но самое главное, это максимальное значение может десятки тысяч раз превышать минимально возможные значения
, что носит условный характер. Но самое главное, это максимальное значение может десятки тысяч раз превышать минимально возможные значения 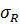 , а разрушения не произойдёт. Для преодоления этой коллизии предложено последовательно снижать предел выносливости, придав вероятностную трактовку характеристике
, а разрушения не произойдёт. Для преодоления этой коллизии предложено последовательно снижать предел выносливости, придав вероятностную трактовку характеристике 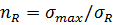 и связав её со временем наработки t [7]. В такой методике, получившей название «метод квантиля»[8], устанавливается сразу ВБР, хотя продуктивнее было бы предварительно получить функцию распределения долговечностей. Последняя, являясь обратной функции вероятности отказа, служит исходной для получения изменения ВБР во времени R(t).
и связав её со временем наработки t [7]. В такой методике, получившей название «метод квантиля»[8], устанавливается сразу ВБР, хотя продуктивнее было бы предварительно получить функцию распределения долговечностей. Последняя, являясь обратной функции вероятности отказа, служит исходной для получения изменения ВБР во времени R(t).
Проблема могла бы решаться довольно просто, если в качестве значения 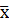 принять некое эквивалентное напряжение
принять некое эквивалентное напряжение 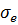 , методики получения которого хорошо отработаны. Но тогда возникает вопрос, как установить его вариацию. Предлагается коэффициент вариации этого внешнего фактора принимать по вариации величины
, методики получения которого хорошо отработаны. Но тогда возникает вопрос, как установить его вариацию. Предлагается коэффициент вариации этого внешнего фактора принимать по вариации величины  равной 0,1, или же приравнять его вариации предела выносливости [7]. Оба варианта безосновательны.
равной 0,1, или же приравнять его вариации предела выносливости [7]. Оба варианта безосновательны.
Наряду с нелогичностью подхода, основной недостаток метода оценки надёжности при постепенных отказах как вероятностной прочности связан с невозможностью корректного учёта фактора времени, поскольку моделирование деградационного процесса предполагается не случайными процессами, а случайными величинами. Поэтому целесообразно оценивать ВБР по кинетическому процессу накопления повреждений посредством сравнения их текущих и допускаемого значений. Подобный метод эффективен, когда диагностический показатель 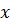 напрямую связан с природой отказа (износ, трещина). Тогда допустимая величина
напрямую связан с природой отказа (износ, трещина). Тогда допустимая величина 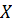 (предельный износ, критический размер трещины) постоянна. В общем же случае предельная величина
(предельный износ, критический размер трещины) постоянна. В общем же случае предельная величина 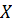 зависит от процесса
зависит от процесса 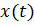 , а кроме этого, для явления усталости она представляется неоднозначно.
, а кроме этого, для явления усталости она представляется неоднозначно.
В связи с этим широко употребимы математико-статистические методы оценки ВБР по интенсивности потока отказов. Например, при независимости случайных процессов изменения факторов 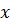 и
и 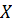 распространены непараметрические экспоненциальные модели:
распространены непараметрические экспоненциальные модели:
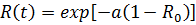 , (2.4)
, (2.4)
где 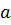 – накопленное повреждение в виде относительной долговечности;
– накопленное повреждение в виде относительной долговечности;
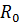 – ВБР при мгновенном отказе.
– ВБР при мгновенном отказе.
Данная модель расходится с экспериментальными данными о распределении долговечностей при значительных повреждениях, порядка a = 0.1 и выше. То есть, когда объект по времени входит в зону эксплуатации с риском, близким к предельному, и необходимо решать вопрос о его эксплуатации или восстановлении.
Подобные модели могут быть построены на основании распределений Вейбулла, Эрланга, усечённому слева, обратному гауссовскому, но для их обоснования необходимо большое количество статистических данных об эксплуатационных отказах. Применительно к уникальным объектам длительного ресурса и повышенного риска такая информация отсутствует.
Для количественной оценки надежности большинство специалистов используют вероятность безотказной работы (ВБР), которая при некоторых допущениях может характеризовать и безопасность R. Изменение ВБР во времени обычно называют функцией надежности или безопасности R(t), которая совместно с алгоритмом ее нахождения, учитывающим количество и вид отказов, образует соответствующую модель.
Процесс эксплуатации характеризуется временем наработки tΣ или числом циклов наработки nΣ , что ведет к накоплению повреждений, мерой которых обычно выступает относительная долговечность: a= tΣ/T= nΣ/N. Для оценки ТС ВБР должна быть чувствительна к этому показателю.
Наиболее часто функцию надежности представляется экспоненциальным уравнением:
Rd=exp(-a)
(основное уравнение надежности по И. А. Биргеру). Оно достаточно чувствительно к наработке (рис.2.2, а), но дает расхождение с экспериментально получаемой функцией распределения долговечностей (ФРД). В частности, наиболее надежно и наименее трудоемко определяемая средняя величина ресурса T должна соответствовать ВБР=0,5. Основное уравнение вычисляет более консервативный результат (табл. 2.1), что приемлемо для стадии проектирования, но не годится для контроля работоспособности. Кроме этого, данный метод не учитывает рассеяние ресурса (т.е. имеет детерминированный характер), и имеет «математическое» происхождение, не связанное с природой деградационного процесса.
В связи с этим функцию надежности или безопасности получают не только приведенным методом потока отказов, но и методом экстраполяции экспериментально обоснованной ФРД в область крайних вероятностей. Полученная таким методом из ФРД нормального типа искомая функция R(t), являясь обратной ФРД, оказывается малочувствительной к наработке и накоплению повреждений, оставаясь, практически горизонтальной на 3/4 периода эксплуатации (рис.2.2, а, линия T(R)). Это делает ее непригодной в качестве диагностического показателя.
Попытки усовершенствовать метод потока отказов, распространив экспоненциальный закон надежности на ситуации со случайным характером моделей нагрузки и прочности, когда Rr=exp[-a(1-R0)] (при этом R0- ВБР для внезапного отказа), устремляют функцию надежности в горизонтальное положение (табл. 2.1).
Рис. 2.2. Связьмежду ВБР и накопленным повреждением в виде относительной наработки a=t/T, полученные по уравнению надежности Rd и по ФРД T(R) нормального вида (а), а также изменение индекса надежности β при постепенном отказе (б) [9].
Таблица 2.1 Изменение ВБР в процессе эксплуатации, полученные по различным моделям
| a | Rd | Rг (R0=0,9) | RW10 | RW20 | RW |
| 0,25 | 0,779 | 0,975 | ~1 | 0,9999 | 0.996 |
| 0,50 | 0,607 | 0,951 | 0,9999 | 0,993 | 0.939 |
| 0,75 | 0,472 | 0,927 | 0,985 | 0,903 | 0.729 |
| 1,00 | 0,368 | 0,905 | 0,520 | 0,519 | 0.368 |
Более обоснованно использовать для аппроксимации распределения долговечностей иного закона, например, Вейбулла, который после его адаптации для применяемых координат выглядит так:
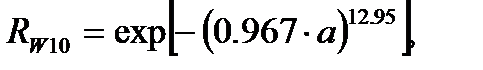 (2.5)
(2.5)
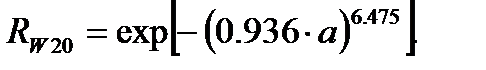 .(2.6)
.(2.6)
Выражения (2.5) и (2.6) получены для коэффициентов вариации ресурса, соответственно, vT=0.1 и vT=0.2 по следующей методике. Параметры распределения Вейбулла
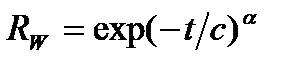
связаны со средним ресурсом Т и его коэффициентом вариации vT как:
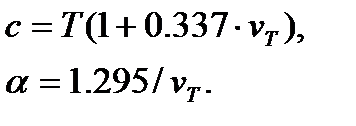
C учетом того, что a=t/T получены вышеуказанные адаптированные выражения.
Однако и в этом случае метод нахождения функций R(t) по ФРД не избавляет функцию надежности от недостатка чувствительности к наработке (табл. 2.1). Более чувствительной к наработке оказывается функция надежности, полученная по закону Вейбулла в форме, рекомендованной для отказов вследствие усталости:
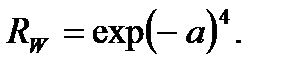
При таком решении наблюдается более компромиссная ситуация (табл. 2.1), но сохраняется тот же недостаток, что и при использовании основного уравнения надежности Rd.
Чтобы избежать этого недостатка используют понятие индекса надежности как функции времени (рис. 2.2, б) [9]:
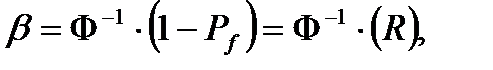 (2.7)
(2.7)
где Ф-функция Лапласа, а Pf –вероятность отказа.
Индекс β , по существу, является нормированным квантилем нормального распределения uR и не отражает физическую природу отказа.
Известно, что трактовка надежности или безопасности как вероятностной прочности корректна при внезапных отказах, и не является таковой при отказах постепенного типа. Для преодоления этой коллизии используют ресурсный подход. Например, Корнелл представляет индекс безопасности как [10]:
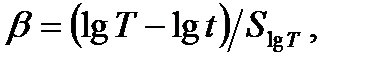 (2.8)
(2.8)
где T и t – соответственно, средняя долговечность и текущая наработка;
SlnT – среднеквадратическое отклонение (СКО) величины lnT.
СКО SlnT определяется с учетом вариаций предельного повреждения, параметра кривой усталости и эквивалентного напряжения для случайного режима нагружения. Тогда по аналогии с (2.7) вероятность отказа постепенного типа будет Pf=Ф(-β).
Индексы надежности и безопасности могут характеризовать ТС в процессе эксплуатации, поскольку более чувствительны к накоплению повреждений и наработке, нежели собственно ВБР. Однако, индекс надежности (2.7) имеет прочностно-силовую трактовку, а индекс безопасности Корнелла (2.8) имеет ресурсно-усталостную трактовку. Поэтому сложно с их помощью сравнивать опасность от внезапных и постепенных отказов. Кроме того, алгоритм поиска распределения величины lnT [10] излишне консервативен, что не дает возможности уточнять ресурс при эксплуатации.
Дата добавления: 2015-03-14; просмотров: 892;
