Теоретичні відомості. Коливання - рухи чи процеси, що мають ту чи іншу міру повторювання в часі
Коливання - рухи чи процеси, що мають ту чи іншу міру повторювання в часі. Вільними є коливання системи, що представлена самою собі у відсутності зовнішнього впливу. Гармонійними називають коливання тіла, зміщення якого від стану рівноваги здійснюється за законом синуса (чи косинуса). Гармонійні коливання здійснюються під дією сили прямо пропорційної зміщенню та направленою до стану рівноваги.
Рівняння вільних коливань для пружинного маятника.
Складемо рівняння гармонійного коливального руху на прикладі вертикального пружинного маятника без урахування сили тертя.
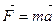 -ІІ закон Ньютона;
-ІІ закон Ньютона;
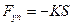 , де
, де 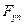 - сила пружності, К- коефіцієнт пропорційності,
- сила пружності, К- коефіцієнт пропорційності, 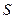 - зміщення тіла від положення рівноваги. Знак « - « показує, що
- зміщення тіла від положення рівноваги. Знак « - « показує, що 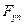 направлена у сторону, протилежну зміщенню тіла.
направлена у сторону, протилежну зміщенню тіла.
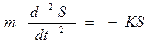 або
або 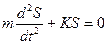 .
.
Отримуємо диференційне рівняння ІІ порядку, яке представлено у вигляді:
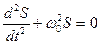 , (3.1)
, (3.1)
де 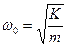 .
.
Рішенням цього диференційного рівняння є:
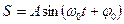 , де (3.2)
, де (3.2)
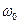 - циклічна частота. Величина амплітуди (А) і початкової фази (
- циклічна частота. Величина амплітуди (А) і початкової фази ( 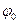 ) визначаються початковим зміщенням та швидкістю тіла. Період коливань пружинного маятника:
) визначаються початковим зміщенням та швидкістю тіла. Період коливань пружинного маятника:
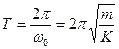
При вільних коливаннях в реальній системі діє сила тертя 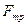 , яка при невеликих швидкостях прямо пропорційна швидкості руху тіла
, яка при невеликих швидкостях прямо пропорційна швидкості руху тіла 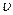 .
.
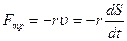 , де
, де
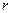 - коефіцієнт пропорційності.
- коефіцієнт пропорційності.
Знак « -« показує, що сила тертя направлена у сторону, протилежну швидкості.
Тоді для вільних коливань можна записати:
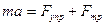 ,
,
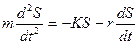 ;
;
звідки маємо:
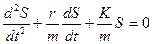
Це лінійне однорідне диференційне рівняння другого порядку, якому можна надати вигляд:

(3.3)
Рішення цього рівняння:
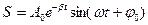 , (3.4)
, (3.4)
де 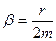 (3.5)
(3.5)
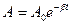 (3.6)
(3.6)
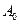 - початкова амплітуда,
- початкова амплітуда, 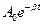 - амплітуда затухаючого коливання,
- амплітуда затухаючого коливання, 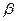 - коефіцієнт затухання.
- коефіцієнт затухання.
Швидкість затухання коливань характеризується коефіцієнтом затухання та декрементом затухання 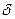 -величиною, яка визначається відношенням любих двох амплітуд, що відстоять одна від одної на один період Т коливання.
-величиною, яка визначається відношенням любих двох амплітуд, що відстоять одна від одної на один період Т коливання.

Доцільно користуватися логарифмічним декрементом затухання:
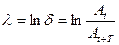 , (3.7)
, (3.7)
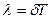 (3.8)
(3.8)
Тобто коефіцієнт затухання можна визначити за допомогою логарифмічного декременту затухання, керуючись графіком коливання.
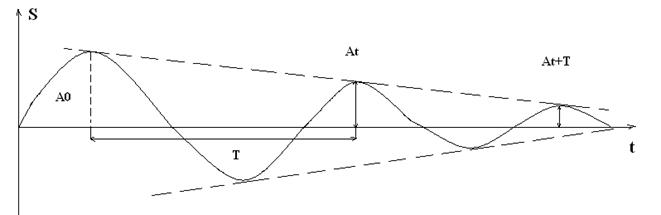
Малюнок 3.9- Графік вільних коливань
Коливальний процес у контурі можна охарактеризувати як періодичний перехід енергії електричного поля конденсатора С в енергію магнітного поля котушки L, і навпаки. У реальному коливальному контурі маємо активний опір R, де втрачається потужність, тому коливання, визвані одноразовим зарядом конденсатора, будуть затухаючими (вільні коливання). За законом Кіргофа для любого замкнутого контуру сума падіння напруги на всіх ділянках дорівнює ЕРС, включеній в цей контур, тобто 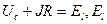 -ЕРС самоіндукції в котушці L,
-ЕРС самоіндукції в котушці L, 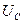 - напруга на конденсаторі,
- напруга на конденсаторі, 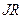 - падіння напруги на активному опорі R. Із визначення сили струму маємо
- падіння напруги на активному опорі R. Із визначення сили струму маємо 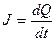 , де
, де 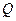 - заряд конденсатора,
- заряд конденсатора, 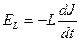 . Тому рівняння для контуру має вигляд:
. Тому рівняння для контуру має вигляд:
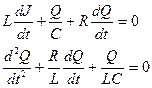 чи
чи
Введемо позначення 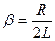 (3.9)
(3.9)
та 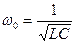 (3.10 )
(3.10 )
Тоді рівняння вільних коливань в контурі матиме вигляд:
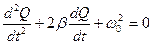 (3.11)
(3.11)
Рівняння 3.11 аналогічно рівнянню 3.3 для вільних механічних коливань. Його рішення можна записати у вигляді:
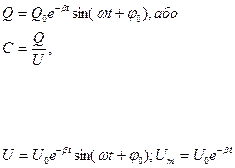 (3.12)
(3.12)
(3.13)
де 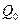 - максимальна амплітуда заряду конденсатора,
- максимальна амплітуда заряду конденсатора, 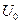 - максимальна амплітуда напруги на конденсаторі.
- максимальна амплітуда напруги на конденсаторі.
Дата добавления: 2015-03-14; просмотров: 833;
