Стационарные состояния в квантовой механике.

Ранее нами уже было получено нестационарное уравнение Шрёдингера, являющееся центральным уравнением квантовой механики. Оно описывает нестационарные, протекающие во времени процессы. Для получения нестационарного уравнения Шрёдингера, необходимо преобразовать выражение:

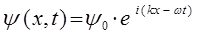
к виду, используя соответствие между импульсом и волновым вектором, энергией и циклической (круговой) частотой, т.е.

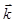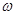тогда соответствующее выражение для плоской волны де Бройля, с учётом этих условий, после подстановки значений и , перепишется в виде:

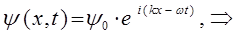
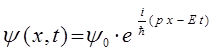
Поскольку гамильтониан есть дифференциальный оператор, то очевидно для нестационарных процессов, его действие при решении задачи на собственные значения оператора будет сводиться к нахождению частной производной по времени от функции .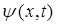

Так, имеем соответственно:

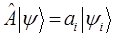
при этом учитывая, что значение амплитуды волны де Бройля 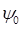будет находиться и в правой, и в левой частях тождества и как следствие сократится, тогда соответственно:

откуда:

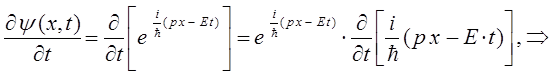
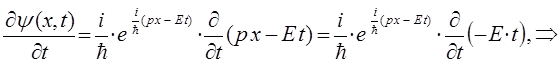
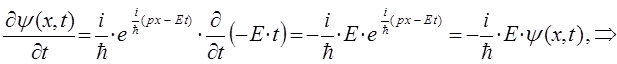
Поскольку:

тогда:

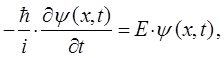
учитывая, что:

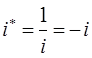
будем иметь соответственно:

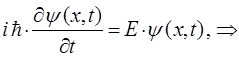
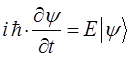
постоянство энергии 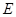позволяет сделать замену вида:

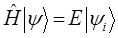
тогда соответственно:

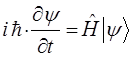
Таким образом, в ходе проделанных выкладок приходим к двум эквивалентным друг другу уравнениям:

Полученные уравнения справедливы для произвольного гамильтониана, допускающего явную зависимость от времени. Уравнение Шрёдингера как линейное дифференциальное уравнение второго порядка в частных производных, имеет бесчисленное множество решений. Из них интерес представляют лишь такие, которые удовлетворяют требованиям регулярности и граничному условию. В обычных задачах квантовой химии при интерпретации свойств и структуры молекул, как правило, важны стационарные (не зависящие от времени) состояния. В стационарных состояниях плотность вероятности, электронная плотность, а также и другие физические величины не зависят от времени. Можно показать, что нестационарное уравнение Шрёдингера:

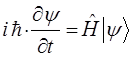
сводится к стационарному (не зависящему от времени) уравнению Шрёдингера. Для этого запишем волновую функцию для электрона, находящегося в стационарном состоянии:

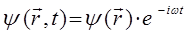
учитывая условия вида:

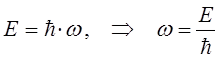
будем иметь соответственно:

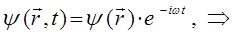
Подставляя данное выражение в нестационарное уравнение Шрёдингера:

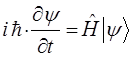
будем иметь соответственно:

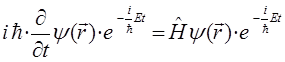
продифференцируем левую часть данного операторного уравнения:

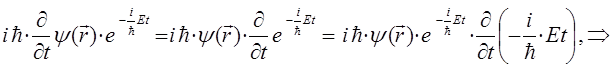
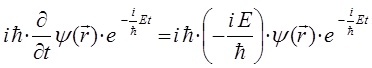
поскольку:

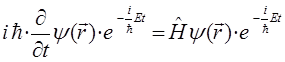
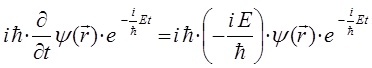
тогда соответственно будем иметь:

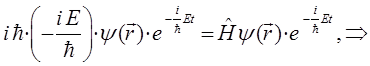
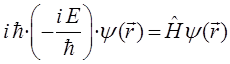
учитывая, что:

находим, что:

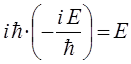
и, следовательно:

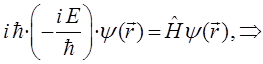
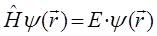
или

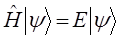
Полученное выше нестационарное уравнение Шрёдингера:

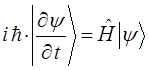
в общем случае справедливо для произвольного гамильтониана, допускающего явную зависимость от времени, например:

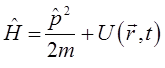
описывая эволюцию квантово-механической системы в поле произвольного потенциала 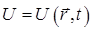. Из нестационарного уравнения вычисляют зависимость от времени любого среднего значения, а, следовательно, и наблюдаемых, собственных чисел операторов динамических величин.

Действительно:

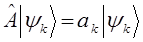
умножая правую и левую части операторного уравнения на бра-вектор :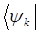

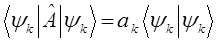
а также учитывая, что:

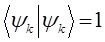
будем иметь соответственно:

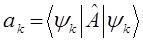
Используя формулу вычисления среднего динамической величины, найдём производную, взятую по времени от выражения:

тогда:

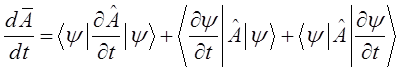
поскольку:

или с учётом того, что:

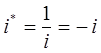
имеем:

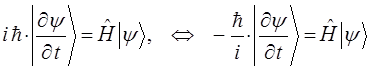
откуда соответственно:

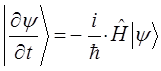
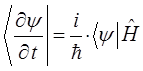
Подставив полученные выше выражения:

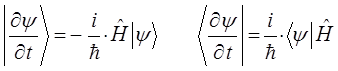
в уравнение:

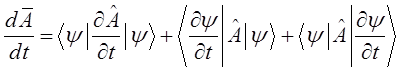
получим:

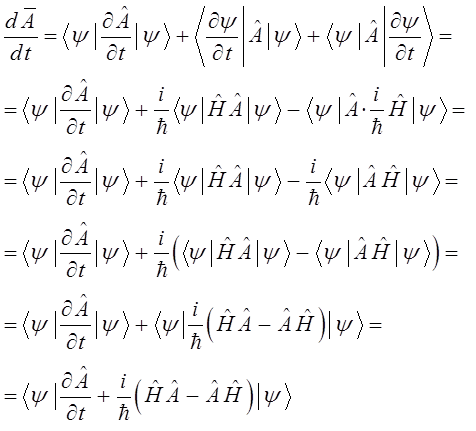
и таким образом:

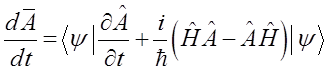
В общем случае, производную 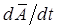можно воспринимать как среднее от оператора 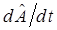, тогда соответственно:

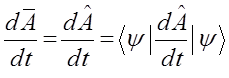
Сравнение выражений:

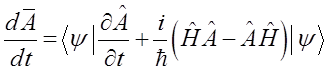
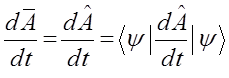
приводит к выражению:

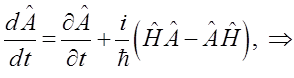
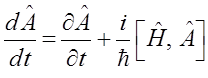
Полученный результат есть аналог классических скобок Пуассона, о которых говорилось в начальных главах данной работы:

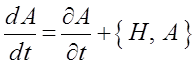
Это позволяет, в свою очередь, второй член в выражении:

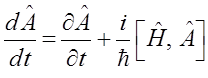
интерпретировать как квантовые скобки Пуассона, определив их равенством:

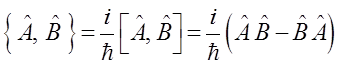
следовательно, зависимость от времени:

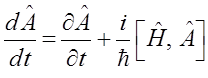
оказывается формально неотличимой от классического аналога данного выражения:

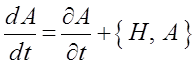
Возможность трактовки коммутационного соотношения как квантовые скобки Пуассона, позволяет переписать первое выражение, представив последнее к виду:

Поскольку наиболее чаще всего явной зависимости от времени нет, т.е.

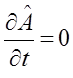
тогда:

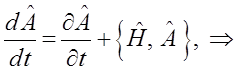
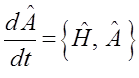
Из полученного выражения становится хорошо видно условие независимости наблюдаемых величин, т.е. собственных чисел 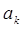от времени:

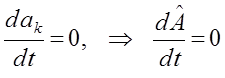
что в свою очередь означает:

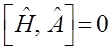
Иными словами, в квантовой механике динамическая величина 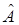будет являться интегралом движения лишь в том случае, если оператор 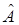коммутирует с гамильтонианом 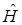. Теперь мы подошли к принципиальному вопросу квантовой механики – проблеме стационарных состояний. Так, например, если классическая система консервативна, то 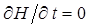, а, следовательно, и 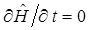. Действительно, учитывая, что:

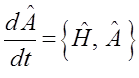
откуда:

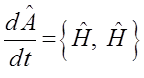
Последнее выражение представляет собой закон сохранения энергии в квантовой механике. Он означает постоянство во времени всех собственных чисел гамильтониана – энергий 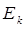, определяемых уравнением:

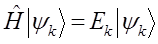
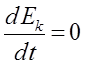
Состояния, энергия которых не зависит от времени, называются стационарными. Сами волновые функции стационарных состояний от времени не зависят. Чтобы установить их вид, заменим правую часть нестационарного уравнения Шрёдингера:

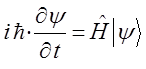
правой частью уравнения:

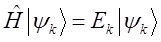
тогда:

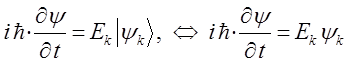
Преобразуя полученное выражение, будем иметь соответственно:

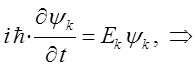
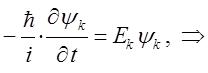
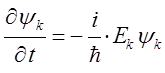
Интегрирование полученного выражения по времени и обозначая постоянную (константу) интегрирования через величину 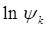, будем иметь соответственно:

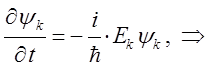
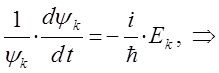
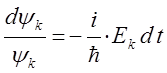
или после интегрирования полученного выражения:

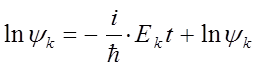
получаем общий вид решения:

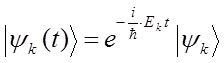
где вектор состояния 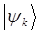от времени зависеть уже не будет, определяясь только пространственными координатами. В частности:

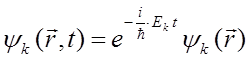
Подстановка полученного общего решения:

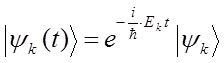
в операторное уравнение:

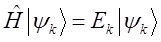
показывает, что:

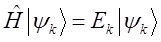
где время уже не участвует. Действительно, подстановка выражения для 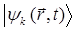в соответствующее операторное уравнение показывает, что:

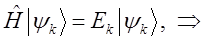
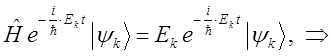
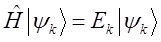
Следовательно, 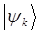удовлетворяют стационарному уравнению Шрёдингера. К подобному выводу мы приходили уже неоднократно – собственно в начале данного раздела и ранее, при обсуждении основных математических подходов и физических аналогий, позволяющих вывести волновое уравнение Шрёдингера, в том числе и вопросов касающихся сведения нестационарного уравнения к стационарному.