Вывод по проведенной лабораторной работе
В результате проведения лабораторной работы мы измерили напряжение диода, рассчитали СКО и определили, что осциллограф применён допустимо правильно, т.к. погрешность допустимая по НД = 0,1066 В, а погрешность данного прибора равна 0,152 В, с учетом предела допустимой погрешности для осциллографа классом точности 3 - = ±3 В.
Варианты и исходные данные для выполнения лабораторной работы
| № по списку группы | Напряжение, (В) | № по списку группы | Напряжение, (В) |
| 75,3 | 60,1 | ||
| 73,5 | 59,0 | ||
| 71,5 | 59,9 | ||
| 75,1 | 58,0 | ||
| 70,2 | 58,9 | ||
| 72,0 | 57,9 | ||
| 69,5 | 57,7 | ||
| 68,5 | 58,7 | ||
| 67,5 | 59,6 | ||
| 66,5 | 59,7 | ||
| 65,6 | 56,9 | ||
| 64,5 | 56,8 | ||
| 63,5 | 56,7 | ||
| 62,5 | 56,6 | ||
| 61,5 | 56,5 | ||
| 60,5 | 55,9 |
Вопросы для самоконтроля
- Понятие "измерение", "методы измерения".
- Методы измерения магнитных величин.
- Основные параметры магнитно-мягких материалов.
- Индукционный метод измерения.
- Феррометрический метод измерения.
- Осциллографический способ измерения.
- Параметрический метод измерения.
- Классификация осциллографов по принципу действия.
- Основные элементы электромеханического осциллографа.
- Электронный осциллограф.
- Электронно-лучевой осциллограф.
- Виды осциллографов.
- Структурная схема осциллографа.
- Характеристика осциллографа-мультиметра С1-107.
- Работа осциллографа.
- Условия поверки осциллографа.
- Этапы поверки.
- Метрологические параметры, определяемые при поверке.
- Оформление результатов поверки.
12 Перечень лабораторных работ раздела 8:
Раздел 8 Измерение электромагнитных величин.
Лабораторная работа № 41 Осциллограф
13 Раздел 9. Измерение колебаний
13.1 Измерение колебаний механических величин
13.1.1 Моделирование механических колебаний
Рассмотрим процесс колебаний груза массы m веса P, подвешенного вертикально на упругой пружине, рисунок 9.1а, где изображены в комплексе и модель колебаний. В состоянии равновесия груз находится на расстоянии yо от точки подвеса. Из рисунка ясно видно, что если оттянуть груз вниз на величину Δy, для этого необходимо приложить механическое воздействие, Δy = y - yо, а затем отпустить груз, то он начнёт колебаться относительно равновесного положения yо. Для изучения процесса колебаний необходимо описать его математически.
Для этого необходимо воспользоваться вторым законом И. Ньютона (произведение массы тела на ускорение равно сумме сил, действующих на тело).
В данном случае на груз действует сила веса P, направленная вниз, и сила упругости пружины, направленная вверх и равная произведению коэффициента упругости k на отклонение груза Δy от равновесного положения. Если обозначить ускорение груза через ay, то можно написать уравнение движения его в виде:
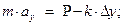 (13.1)
(13.1)
Решить это уравнение, значит, найти, как в процессе движения будут изменяться координата груза y, его скорость υy, ускорение ay и каков будет период колебаний Т.
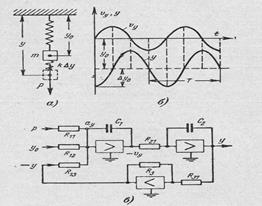
Рисунок 13.1 Моделирование механических колебаний
а) – механическая колебательная система с грузом и пружиной;
б) – графики изменения координаты y и скорости υy груза;
в) электронный аналог механической системы как модель процесса.
Задача, как правило, решается при конкретных значениях P, m, k, yо и начальном значении отклонения механического воздействия Δyо.
Выразив из уравнения движения ускорение:
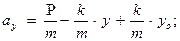 (13.2)
(13.2)
легко видеть, что вычислить ускорение можно с помощью усилителя, на входы которого подаются электрические аналоги величин P, yо и y, если последнюю считать известной. Если этот усилитель выполняет операцию интегрирования, то на его выходе можно получить электрический аналог скорости с обратным знаком, а именно - υy. Эту величину можно ещё раз проинтегрировать с помощью второго решающего усилителя и получить аналог координаты y, который по цепи обратной связи через блок перемены знака подаётся на вход первого усилителя.
Таким образом, схема решения поставленной задачи будет иметь вид, представленный на рисунке 13.1в.
Если принять все масштабные коэффициенты равными единице, то для элементов схемы справедливы следующие соотношения:
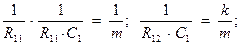 (13.3)
(13.3)
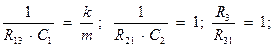 (13.4)
(13.4)
Регистрируя изменение напряжений на выходах решающих усилителей, можно получить графики изменения υy и координаты y, а по ним определить период колебаний Т, рисунок 13.1б.
Рассмотренная схема позволяет моделировать колебания любой физической природы (механические, электрические, звуковые, ультразвуковые и т.д.), при условии, что они описываются аналогичными уравнениями.
Второй подход к механическим колебаниям - геометрические соображения.
Вместо того чтобы подвешивать груз на пружине или нити и заставлять его качаться, прикрепим груз к ободу вращающегося колеса. на первый взгляд не видно, как вращательное движение связано с колебательным, хотя можно заметить, что в обоих случаях груз регулярно возвращается в одну и ту же точку и повторяет своё движение с определённой частотой. Если наблюдать вертикальную проекцию перпендикулярно на плоскость или ось x вращающегося груза, то схожесть этих двух движение становится вполне понятной. Угловое положение груза задаётся углом Θ = ωt , где ω - угловая скорость. Положение проекции груза на ось x даётся величиной x = r · sin Θ = r · sin ωt.
На рисунке 13.2 это явление хорошо иллюстрируется.
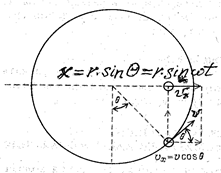
Рисунок 13.2 Проекция точки на ось вращающегося груза
Нетрудно заметить, что эти геометрические соображения автоматически как бы приводят колебания к синусоидальной форме зависимости положения груза от времени. Тангенциальная сила массы груза и скорость вращающегося груза всегда постоянна по модулю, но меняется по знаку – по направлению. Проекция вектора скорости равна vx = v · cos Θ = v · cos ωt = r · ω · cos ωt; где v = r · ω;
Остаётся определить ускорение проекции груза, который вращается с постоянной угловой скоростью. Известно, что во всех случаях, когда на тело действует сила, подчиняющаяся закону F = − kx , оно совершает колебательное движение. Период колебания – время, за которое совершается полный цикл, - может быть найден из геометрических соотношений между вращательным и колебательным движениями. Ускорение при колебании α = −ω v = − ω2 r sin ωt; А угловая скорость может быть выражена через вращение 2πf или 2π/T. Радиус вращательного движения обычно равен амплитуде колебаний, которая выражается обычно обозначением буквы А, поэтому выражение ускорения можно переписать – α = − ω2 А sin ωt ; Центробежное смещение колеблющегося груза имеет вид F=mα=−kx; После подстановки имеющихся значений, можно получить преобразованные выражения: m (− ω2 A sin ωt) = − k (A sin ωt); Здесь видно множитель A sin ωt и знак минус, которые можно сократить, тогда имеем более короткое выражение m ω2 = k;, а из этого можно вычислить значение частоты и периода колебаний: f = (1/2 π)·√k ⁄ m; T = 2π √m ⁄ k; Следует обратить внимание на то, что в формуле периода колебания масса груза в числителе, следовательно, чем больше масса груза, тем больше его инерция и менее податлив он для усилия перемещения цикла колебания. Жесткость пружины k входит в знаменатель, поэтому сильная пружина имеет большее значение k и быстрее возвращает груз в положение равновесия по сравнению со слабой пружиной.
13.1.2 Третий подход к механическим колебаниям - подвешенный маятник.
Каким образом изменится выражения, если подвесить груз на гибком тросе и заставить его качаться как маятник? Теперь уже нет никакой пружины. Удовлетворяется ли в этом случае требование F = − kx? Покажем на рисунке силы, действующие на груз маятника:
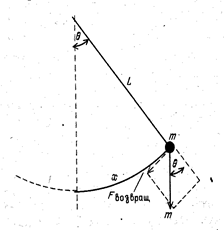
Рисунок 13.3 Возвращающая сила груза массой m.
Сила тяжести разбивается на две составляющие – радиальную, направленную вдоль троса, и тангенциальную, направленную по линии движения. Тангенциальная составляющая силы сообщает грузу ускорение в направлении положения равновесия: Fвозвращ = ─ mg sin Θ = ─ mg sin (x/L); Однако это не то соотношение, которое было бы необходимо. Вместо того чтобы получить возвращающую силу, пропорциональную смещению, взятому со знаком минус, мы получили возвращающуюся силу, пропорциональную взятому с обратным знаком синусу смещения параметра отклонения к длине троса маятника. Если в этом случае взять предположение малости углов отклонения маятника при которых будет обеспечиваться равенство: sin Θ ≈ 0; , то тогда:
Fвозвращ. ≈ ─ mg (x/L )= ─ (mg/L) x; k = mg/L; Fв. = ─ kx;
В результате этих рассуждений ясно, что закон изменения силы имеет тот же вид с коэффициентом пропорциональности. Период колебания маятника при малых углах отклонения будет иметь следующий вид:
T = 2π √m / k = 2π √m / mgL = 2π √L / g;
Следует обратить внимание, что период колебания маятника не зависит от массы груза, если не учитывать массу троса подвеса, считая её бесконечно малой величиной по сравнению с массой груза. Однако, если такая необходимость возникнет, то тогда будет необходимо учитывать моменты инерции и центры масс конструкции маятника.
13.1.3 Простые гармонические колебания и другие виды колебаний.
Во всех случаях, когда система может колебаться около равновесного положения и действующая на неё сила пропорциональна смещению от центра колебаний, движение является синусоидальным, и оно называется простым гармоничным колебанием (ПГК). Простое оно потому, что прост закон изменения силы и потому, что происходит только с одной частотой. А гармоничным оно называется в том смысле, что происходит от музыкальных теорий и инструментов в музыке, так как основная нота может быть основой для гармонических обертонов.
КОЛЕБАНИЯ -движения или процессы, обладающие той или иной степенью повторяемости. Колебания могут быть периодическими, когда в результате нарушения состояния равновесиявозникают изменения состояния физической системы, повторяющиеся через равные промежутки времени, называемые периодом колебаний, и апериодическими, когда нет полного повторения процесса изменения. Различают механические колебания, (например, колебания маятника, струны, моста, корабля на волне, плотности и давления воздуха при распространении звука и т.д.), электромагнитные колебания (например, колебания электрических и магнитных полей, возбуждающиеся в колебательном контуре, распространяющиеся в виде волн в пространстве, в волноводах и др.) и их комбинации. Колебания различной природы подчиняются общим закономерностям. Простейшим видом колебаний являются гармонические колебания. Эта выдержка из энциклопедического словаря / 41/.
13.2 Измерение колебаний электрических величин
Рассмотрение измерений электрических колебаний подробно проводится в седьмом разделе при изучении измерений напряжений и токов переменных значений. Поэтому в данном разделе приходится переадресовывать материал в раздел №7 и в раздел № 8,10. В разделах 8 и 10 рассматривается подробно вид колебаний в виде электромагнитных явлений и частоты проявляющихся в различных технических проблемах деятельности человеческого общества и в приборостроительной индустрии. Так для изучения измерений электротехнических колебаний создаются соответствующие измерительные генераторы, которые могут быть генераторами гармонических колебаний, негармонических - специальных колебаний, звуковых генераторов, сверхвысокочастотных генераторов, генераторов ультразвуковой частоты, акустические генераторы, генераторы частот настройки часов и т.д.
13.2.1 Колебательный контур-замкнутая электрическая цепь, содержащая катушку с индуктивностью L, конденсатор с ёмкостью С и электрическое сопротивление R, в которой могут возбуждаться электрические колебания.В колебательном контуре дважды за период происходит перекачка энергии из электрического поля конденсатора в магнитное поле катушки индуктивности и обратно. При этом часть энергии теряется на преодоление сопротивления проводников цепи R, переходя в тепло, что приводит к затуханию колебаний. Если R мало, то затухание слабое и частота колебаний колебательного контура близка к частоте собственных колебаний: ω0 = 1/√LC;
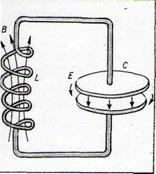
Рисунок 13.4 Колебательный контур: L - индуктивность; C - ёмкость; E - электрическое поле; B - магнитное поле.
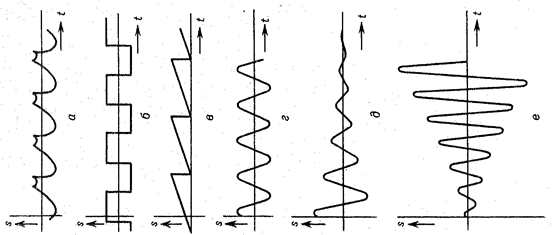
Рисунок 13.5 электрические колебания: а) Периодические сложной формы;
б) Прямоугольные; в) Пилообразные; г) синусоидальные; д) Апериодические
(затухающие); е) Нарастающие; Здесь: S - смещение; t - время.
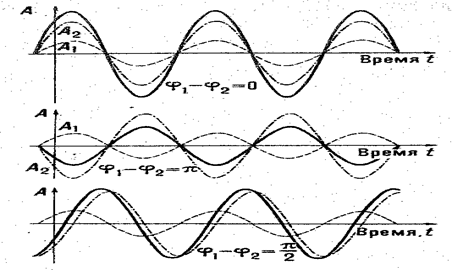
Рисунок 13.6 Когерентность колебаний: Сложение двух гармонических колебаний (пунктир) с амплитудами А1 и A2 при различных разностях фаз (φ1;φ2).
Результирующее колебание - сплошная линия.
13.2.2 Когерентность - (от латинского слова cohaerens, род. п. cohaerentis - пребывающий во взаимной связи), согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов (любой природы), проявляющееся при их сложении. Колебания называются когерентными, если разность их фаз остаётся постоянной (или закономерно изменяется) во времени. Когерентность - необходимое условие интерференции волн.В более широком смысле понятие - «когерентность» применяется в различных областях физики для описания коррелированного (согласованного) поведения большого числа частиц.
13.2.3. Демпфирующее устройство.
В электрических измерительных приборах (системах) применяются тормозящие устройства - демпферы, существуют и в механических системах пружинные устройства с демпфированием частоты колебаний, так называемые «успокоители колебаний». Этот процесс имеет теоретический аспект, который будет рассмотрен ниже, после показа иллюстрирующих рисунков.
| 
|
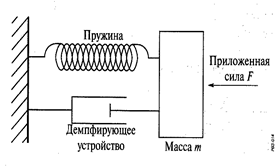
Рисунок 13.7 Демпфирующее устройство прибора или системы успокоения.
Многие системы (механические, электрические, радиоэлектронные и т.д.) второго порядка можно свести к системам, имеющим три основных элемента: массу т, пружину и демпфирующее устройство. Результирующая сила, действующая на массу, равна разности приложенной силы F, силы упругости пружины (либо от ее растяжения, либо от сжатия) и силы демпфирующего устройства. Сила упругости от сжатия и растяжения пружины пропорциональна изменению ее длины x, т.е. ее можно представить в виде kx, где k - коэффициент жесткости пружины. В качестве демпфирующего устройства можно представить себе конструкцию, состоящую из поршня, двигающегося в цилиндре, заполненном маслом. Тогда сила от демпфирующего устройства будет пропорциональна скорости перемещения поршня, которую можно представить в виде c(dx/dt), где c - константа. Таким образом, результирующую силу R, действующую на массу m,можно представить как:
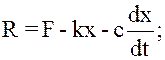 (13.5)
(13.5)
По второму закону Ньютона эта сила заставляет массу двигаться с ускорением. Так как ускорение - это производная скорости (dv/dt), а скорость - это производная перемещения (dx/dt), то ускорение - это вторая производная перемещения (d2 x/dt2). Следовательно, будем иметь следующее выражение:
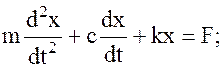 (13.6)
(13.6)
В случае отсутствия демпфирующего устройства масса, прикрепленная к концу пружины, будет свободно колебаться с собственной частотой ωп, определяемой в виде:
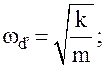 (13.7)
(13.7)
Если колебания затухают с коэффициентом затухания ζ, определяемым как:
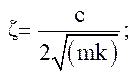 (13.8)
(13.8)
После такого преобразования уравнение приобретает следующий вид:
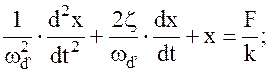 (13.9)
(13.9)
Теперь можно считать, что теоретические предпосылки по колебаниям достаточно исчерпаны.
Для организации лабораторных работ по разделу № 8 измерения электромагнитных величин на кафедру МСиС ТФ ГОУ ОГУ приобретена лабораторная установка «Методы измерения электрических величин МСИ 6», - паспорт МСИ 6 ПС от Министерства образования РФ ФГО ООО «ИНТОС+» заводской № 009 по ТУ 9.461 – 2004 дата изготовления и упакована для отправки в ГОУ ОГУ на кафедру МСиС ТФ 15.09 2008 года:
1 Назначение
Установка лабораторная «Методы измерения частоты МСИ 6» (далее -установка) является частью учебно-лабораторного комплекса, используемого для проведения лабораторных работ при изучении дисциплины «Методы и средства измерений, испытаний и контроля» для специальности 200503 – Стандартизация и сертификация и 220501 – Управление качеством.
Установка должна эксплуатироваться в помещениях при температуре воздуха от+ 10°Сдо + 35°С, относительной влажности воздуха до 80 % при 25 ° С.
2 Основные технические данные
Установка предназначена для формирования частот заданного спектра в электрической и оптической формах, измерение частоты промышленными приборами
| 220 ± 22 50 ± 0, 4 не более 5 |
2.1 Питание от сети переменного тока:
- напряжением, В
- частотой, Гц
2.2 Потребляемая мощность, В А
2.3 Характеристики
| 5,0 ±0,5 1,0±0,1 5, 0 ±1,0 0, 5 ± 0, 2 не более 200 не более 150 не более 100 не более 1, 0 не менее 1000 |
2.3.1 Максимальное значение формируемой
частоты, кГц
2.3.2 Минимальное значение формируемой
частоты, кГц
2.3.3 Максимальное значение напряжения
электрического сигнала, В
2.3.4 Минимальное значение напряжения
электрического сигнала, В
2.5 Габаритные размеры установки, мм
длина
ширина
высота
2.6 Масса установки, кг
2.7Средняя наработка до отказа, ч
2.8 Средний срок службы до списания, лет
42 Лабораторная работа № 42 ХРОНОМЕТР
(Демонстрационная практическая работа)
Дата добавления: 2015-01-13; просмотров: 3490;
