Выпаривание. Лекция № 2 (16.01.15. - 21.01.15)
S0, S – расход, соответственно, исходного раствора и выпаренного раствора, кг/с;
t0, t – температура исходного и выпаренного растворов, град.;
co, c – теплоемкость растворов, кДж/кг.град;
аo, а – концентрация растворенного вещества, соответственно, в исходном и выпаренном растворах, кг В/кг раств (абсолютная массовая доля);
W, i – соответственно, расход и энтальпия вторичного пара, кг/с, кДж/кг;
Dгр – расход греющего пара (конденсата греющего пара), кг/с;
h, iК – энтальпия, соответственно, греющего пара и конденсата греющего пара;
T – температура греющего пара, К;
d – удельный расход греющего пара, равный отношению D/W, кг гр пара/кг втор пара.
В соответствие с модельными представлениями процесса выпаривания в выпарном аппарате принимают: 1) температура вторичного пара равна температуре кипения растворителя при давлении над кипящим раствором, равным р; 2) структура потока раствора (парожидкостной смеси) в трубном пространстве греющей камеры соответствует модели идеального перемешивания, которая предполагает постоянство состава и температуры раствора во всех точках этого пространства. 3) в ходе выпаривания в паровую фазу переходит только растворитель, растворенное вещество полностью остается в растворе.
Температура кипения раствора, вторичного пара. Температурная депрессия. Правило Бабо. Поправка по таблице Стабникова.
Температура кипения раствора всегда выше температуры кипения чистого растворителя на величину температурной депрессии, 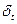 , которая обусловлена свойствами компонентов, составляющих систему (раствор). На рис. 2.1 представлена зависимость температуры кипения раствора от концентрации растворенного вещества для давления в 760 мм рт. ст. над кипящим раствором. Разность между этой температурой и температурой кипения воды (1000С) образует так называемую стандартную депрессию, т.е. депрессию справедливую только для нормального давления над кипящим раствором.
, которая обусловлена свойствами компонентов, составляющих систему (раствор). На рис. 2.1 представлена зависимость температуры кипения раствора от концентрации растворенного вещества для давления в 760 мм рт. ст. над кипящим раствором. Разность между этой температурой и температурой кипения воды (1000С) образует так называемую стандартную депрессию, т.е. депрессию справедливую только для нормального давления над кипящим раствором.
Для определения температурной депрессии при давлениях отличающихся от нормального используют различные способы расчета. Правило Бабо – один из таких способов. Согласно правилу Бабо отношение давлений над раствором и растворителем при одинаковой температуре кипения обоих тел есть величина постоянная для данной концентрации раствора
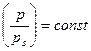 ; или
; или 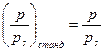 . (1.1)
. (1.1)
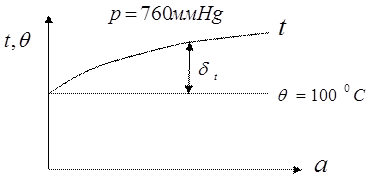 |
Рис. 2.1 Зависимость температуры кипения раствора некоторого вещества в воде при нормальном давлении над кипящим раствором.
Левая часть последнего равенства справедлива для давления над раствором равному нормальному, а правая часть этого равенства – для рабочего давления над раствором, т.е. давления реально существующего в сепараторе выпарного аппарата.
Выше было отмечено, что температура вторичного пара, 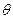 , принимается равной температуре кипения чистого растворителя для данного давления. Следовательно, связь между температурами кипящего раствора и вторичного пара может быть выражена формулой
, принимается равной температуре кипения чистого растворителя для данного давления. Следовательно, связь между температурами кипящего раствора и вторичного пара может быть выражена формулой
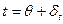 . (2.1)
. (2.1)
Если пренебречь теплотой растворения, тогда теплоемкость раствора может быть рассчитана по правилу аддитивности
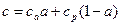 , (3.1)
, (3.1)
где са и ср теплоемкости растворенного вещества и растворителя.
Расчет выпарного аппарата непрерывного действия.
(Определение величины потока вторичного пара, потока выпаренного раствора, потока тепла через поверхность греющей камеры, потока греющего пара, потребной поверхности теплообмена аппарата при известных значениях: расхода исходного раствора, температуры исходного раствора, концентрации исходного раствора, концентрации выпаренного раствора, теплоемкости исходного раствора, давления греющего пара, давление вторичного пара).
Изображаем упрощенную схему выпарного аппарата с указанием материальных и тепловых потоков (рис. 3.1)
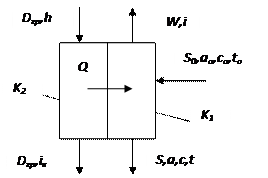 |
Рис. 3.1 Упрощенная схема выпарного аппарата.
Выделяем на упрощенной схеме два контура. Составляем уравнения материального баланса для 1-го контура: по смеси
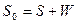 , (4.1)
, (4.1)
по растворенному веществу
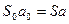 . (5.1)
. (5.1)
Решая совместно эти уравнения, получим
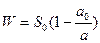 , (6.1)
, (6.1)
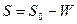 . (7.1)
. (7.1)
Составляем уравнение теплового баланса для 1-го контура, пренебрегая потерями тепла в окружающую среду
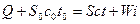 ,
,
откуда
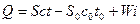 . (8.1)
. (8.1)
Для упрощения полученного выражения воспользуемся правилом аддитивности в следующем виде
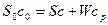 ,
,
откуда
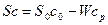 .
.
Подставляя полученное выражение в уравнение (8.1), получим
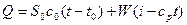 . (9.1)
. (9.1)
Прочтем полученное выражение: потребный тепловой поток складывается из двух составляющих. Первая составляющая это тепловой поток, необходимый для нагревания исходного раствора от начальной температуры до температуры кипения выпаренного раствора. Вторая составляющая это тепловой поток, необходимый для обращения части растворителя во вторичный пар.
Составляем уравнение теплового баланса для второго контура, пренебрегая потерями тепла в окружающую среду
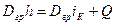 ,
,
откуда
 . (10.1)
. (10.1)
Для определения потребной поверхности теплообмена воспользуемся основным уравнением теплопередачи в виде
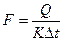 , (11.1)
, (11.1)
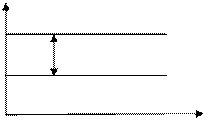 |
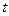
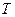
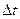
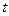
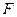
Рис. 4.1 Диаграмма распределения температур греющего пара и кипящего раствора вдоль поверхности теплообмена выпарного аппарата.
где К – коэффициент теплопередачи от конденсирующегося пара к кипящему раствору, а 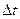 - полезная разность температур между теплоносителями выпарного аппарата (см. рис. 4.1)
- полезная разность температур между теплоносителями выпарного аппарата (см. рис. 4.1)
Для справки:
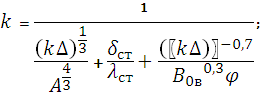
Выбор рабочего давления в выпарном аппарате.
Выбор рабочего давления определяется двумя факторами. Первым фактором является стойкость растворенного вещества к воздействию высоких температур. Т.е., если вещество является термолабильным (лабильный – неустойчивый), тогда давление в аппарате будет определяться допустимой температурой кипения раствора, вплоть до создания в аппарате вакуума.
Вторым фактором является экономическая целесообразность. Т.е., если вещество является устойчивым к воздействию температур (термостабильным), тогда высокое давление в аппарате позволит получить вторичный пар высоких параметров, который может быть использован в других установках.
В то же время, вне зависимости от уровня стойкости растворенного вещества к воздействию высоких температур, всегда целесообразно проведение процесса выпаривания под вакуумом, если есть возможность в использовании греющего пара низких параметров, стоимость которого значительно ниже стоимости греющего пара высоких параметров.
Выпаривание под вакуумом. Схема выпарной установки, снабженная барометрическим конденсатором смешения. Принцип действия барометрического конденсатора смешения. Температурная депрессия, вызванная гидравлическими потерями.
Для получения вакуума в выпарных аппаратах вторичный пар необходимо конденсировать. Для этого вторичный пар направляют либо в поверхностный конденсатор, либо в конденсатор смешения
Поверхностные конденсаторы целесообразно применять в случае, когда в паре содержатся агрессивные вещества, загрязняющие промышленные стоки, или, если в качестве охлаждающего теплоносителя используют, например, исходный раствор. В остальных случаях наиболее целесообразно применение конденсаторов смешения, которые более просты по конструкции, имеют меньшие размеры и менее металлоемки, отличаются простотой ремонта и эксплуатации.
В конденсаторах смешения меньше расход охлаждающей воды, так как они обеспечивают возможность получения более высоких температур смеси (конденсат, охлаждающая вода). Последнее объясняется тем, что разность между температурой конденсации вторичного пара и конечной температурой выходящей смеси в конденсаторах смешения составляет 2 – 3 градуса, а в поверхностных конденсаторах 7 – 10 градусов. Однако конденсаторы смешения требуют более высокого расхода электроэнергии на удаление инертных газов, так как помимо газа, содержащегося в паре, в растворе и попадающем через неплотности воздуха, дополнительно выделяется воздух из охлаждающей воды (в 1 литре воды при температуре 200С содержится 25 мг воздуха).
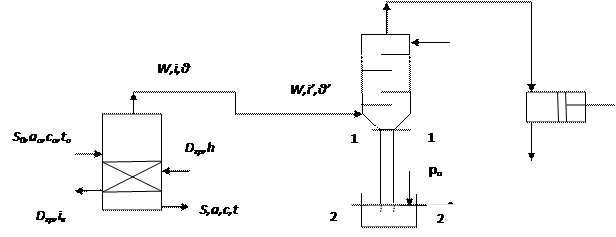
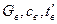
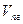
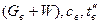
Рис. 5.1 Схема однокорпусной выпарной установки, снабженной барометрическим конденсатором смешения.
Для выпарных установок, предназначенных для выпаривания солесодержащие растворы, наиболее широко применяют конденсаторы смешения. Принцип действия любого конденсатора базируется на существенной разности плотностей пара и конденсата.
Вторичный пар из сепаратора выпарного аппарата направляется под нижнюю полку конденсатора. На верхнюю полку конденсатора поступает охлаждающая вода. Каждая из полок выполнена из стального перфорированного листа с переливными бортиками. С верхней полки вода переливается через бортик и через отверстия полки, попадая на нижележащие полки. Таким образом, создается плотная водяная завеса, препятствующая проскоку пара. Образующаяся смесь конденсата пара и воды отводится из конденсатора по барометрической трубе последовательно сначала в барометрический ящик и далее в линию оборотной воды.
Для отбора парогазовой смеси из верхней части конденсатора используется водокольцевой вакуум-насос.
Расчетными параметрами барометрического конденсатора являются: расход охлаждающей воды, Gв; производительность вакуумного насоса, Vпг; высота барометрической трубы, Нтр, и ее диаметр,dтр.
Для определения расхода охлаждающей воды составим уравнение теплового баланса для 1-го контура, пренебрегая потоком тепла с парогазовой смесью (см. рис. 5.1).
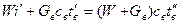 , (12.1)
, (12.1)
где 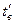 - температура охлаждающей воды на входе в барометрический конденсатор смешения,
- температура охлаждающей воды на входе в барометрический конденсатор смешения, 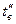 - температура смеси конденсата вторичного пара с охлаждающей водой,
- температура смеси конденсата вторичного пара с охлаждающей водой, 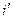 - энтальпия вторичного пара на входе в конденсатор, которая зависит от гидравлических потерь потока вторичного пара на участке «выпарной аппарат – конденсатор», т.е. является функцией температуры вторичного пара на входе в конденсатор,
- энтальпия вторичного пара на входе в конденсатор, которая зависит от гидравлических потерь потока вторичного пара на участке «выпарной аппарат – конденсатор», т.е. является функцией температуры вторичного пара на входе в конденсатор, 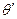 .
.
Рекомендуется использовать оборотную воду в качестве источника охлаждающей воды. Температура оборотной воды на входе в конденсатор для летних условий может быть принята равной 200С (вообще говоря, зависит от географического расположения установки).
Температура смеси охлаждающей воды и конденсата вторичного пара принимается равной температуре вторичного пара на входе в конденсатор за вычетом 2х, 3х градусов
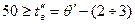 , (13.1)
, (13.1)
(максимальная температура воды ограничена; одна из причин ограничения – интенсивное отложение солей из воды в конденсаторе и в барометрической трубе при температурах превышающих 500С),
где 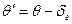 , (14.1)
, (14.1)
при этом, 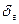 - температурная депрессия, вызванная гидравлическими потерями потока вторичного пара при его движении от сепаратора выпарного аппарата к конденсатору.
- температурная депрессия, вызванная гидравлическими потерями потока вторичного пара при его движении от сепаратора выпарного аппарата к конденсатору.
Согласно уравнению (12.1) расход охлаждающей воды будет равен
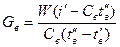 . (15.1)
. (15.1)
Диаметр барометрической трубы определяется по уравнению расхода для потока смеси в барометрической трубе
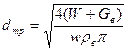 , (16.1)
, (16.1)
где 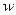 -скорость движения смеси в барометрической трубе, принимаемая равной
-скорость движения смеси в барометрической трубе, принимаемая равной 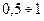 м/с; ρв – плотность смеси охлаждающей воды и конденсата вторичного пара.
м/с; ρв – плотность смеси охлаждающей воды и конденсата вторичного пара.
Высота барометрической трубы определяется с помощью уравнения Бернулли, записанного для сечений «1-1» и «2-2» (см. рис. 5.1)
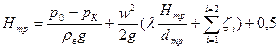 , (17.1)
, (17.1)
где p0 – атмосферное давление; pк – остаточное давление в конденсаторе, определяемое по температуре вторичного пара на входе в конденсатор.
Объемный поток парогазовой смеси, откачиваемой из конденсатора, может быть рассчитан с помощью уравнения Менделеева – Клайперона, записанного для одного из компонентов смеси, а именно – для газа (воздуха)
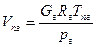 , (18.1)
, (18.1)
где Gг - массовый поток воздуха, определяемый по уравнению
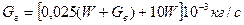 . (19.1)
. (19.1)
Rг – газовая постоянная воздуха, равная 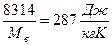 .
.
Tпг – температура парогазовой смеси, равная tпг + 273,
где 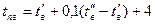 . (20.1)
. (20.1)
pг – парциальное давление газа (воздуха), равное
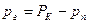 , (21.1)
, (21.1)
где pп – парциальное давление пара, определяемое по температуре парогазовой смеси.
Выпаривание. Лекция № 2 (16.01.15. - 21.01.15)
Однокорпусные выпарные установки имеют существенный недостаток: велик удельный расход греющего пара из расчета на 1 кг вторичного пара.
Содержание лекции.
Многокорпусные выпарные установки (МВУ). Принцип действия прямоточной МВУ. Тепловые балансы МВУ. Полезная разность температур отдельных корпусов. Полная полезная разность температур установки. Располагаемая разность температур установки. Влияние числа корпусов на величину полезной разности температур. Вывод расчетного выражения для определения поверхности теплообмена одного корпуса МВУ при условии справедливости равенства 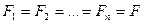 .
.
Многокорпусные выпарные установки (МВУ). Принцип действия прямоточной МВУ. Тепловые балансы МВУ.
Принцип действия МВУ базируется на использовании вторичного пара предшествующего корпуса в качестве греющего пара в последующем. Таким образом, сокращается удельный расход первичного греющего пара, т.е. пара поступающего в первый корпус МВУ. Сокращение удельного расхода первичного греющего пара будет пропорционально числу корпусов МВУ, если предположить, что на каждый кг греющего пара в каждом корпусе МВУ приходится кг вторичного пара, т.е. 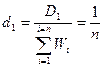 , где n – число корпусов МВУ.
, где n – число корпусов МВУ.
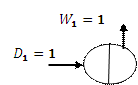 В самом деле, если число корпусов равно 1, а
В самом деле, если число корпусов равно 1, а  тогда
тогда 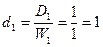 (см. рис.).
(см. рис.).
|
|
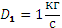 , тогда
, тогда 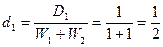 (см. рис.)
(см. рис.)

Если число корпусов равно 3, а 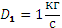 , тогда
, тогда 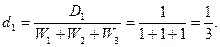
На самом деле, с учетом термодинамики процесса и потерь тепла в окружающую среду, удельный расход первичного греющего пара всегда выше «идеализированного».
Непременным условием реализации процесса выпаривания в МВУ является постепенное понижение давления над кипящим раствором от первого корпуса к последнему ( 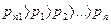 ).
).
На рис. 1.2. представлена принципиальная схема прямоточной МВУ, снабженная подогревателем исходного раствора, тремя выпарными аппаратами, барометрическим конденсатором смешения и вакуумным насосом.
Исходный раствор после нагревания его в подогревателе поступает в первый корпус МВУ, где происходит концентрирование его до промежуточной концентрации. Часть вторичного пара первого корпуса служит греющим паром для второго. Другая часть вторичного пара используется в качестве экстра – пара (пара «на сторону»).
Выпаренный раствор из первого корпуса переходит во второй за счет разности давлений между первым и вторым. Здесь происходит его последующее концентрирование до второй промежуточной концентрации. Вторичный пар второго корпуса служит греющим паром для третьего.

Рис. 1.2. Принципиальная схема прямоточной МВУ: 1 – подогреватель исходного раствора; 2 – первый корпус МВУ; 3 – второй корпус; 4 – третий корпус; 5 – барометрический конденсатор; 6 – вакуумный насос.
Выпаренный раствор из второго корпуса самопроизвольно перетекает в третий (преимущество прямоточной схемы МВУ). Здесь происходит его окончательное концентрирование до финальной концентрации. Вторичный пар третьего корпуса поступает в барометрический конденсатор смешения, благодаря чему в этом корпусе создается самое низкое давление установки.
Уравнения тепловых балансов МВУ.
Для первого корпуса
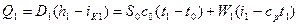 .
.
Для второго корпуса
 ,
, 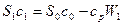 .
.
Для третьего корпуса
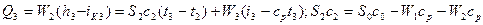 .
.
Прочтение каждого из уравнений теплового баланса можно выполнить по аналогии с прочтением уравнения (9.1).
Полезная разность температур отдельных корпусов. Полная полезная разность температур установки. Располагаемая разность температур установки. Влияние числа корпусов на величину полезной разности температур.
Полезная разность температур первого корпуса
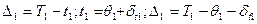 . (1.2)
. (1.2)
Полезная разность температур второго корпуса
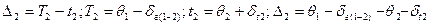 . (2.2)
. (2.2)
Полезная разность температур третьего корпуса
 . (3.2)
. (3.2)
Полная полезная разность температур МВУ (3 корпуса)
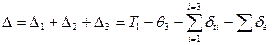 (4.2)
(4.2)
Полная полезная разность температур МВУ для произвольного числа корпусов n
 (5.2)
(5.2)
Располагаемая разность температур
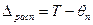 , (6.2)
, (6.2)
таким образом
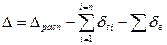 . (7.2)
. (7.2)
Сравнивая полезную разность температур для МВУ различного числа корпусов при условии, что располагаемая разность одинакова для любого МВУ, приходим к очевидному выводу: полезная разность температур МВУ с ростом числа корпусов падает за счет роста сумм температурных депрессий различного рода.
Вывод расчетного выражения для определения поверхности теплообмена одного корпуса МВУ при условии справедливости равенства 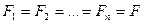 .
.
Воспользуемся уравнением (4.2) для решения поставленной задачи на примере МВУ с тремя корпусами. 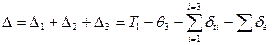
На рис. 2.2 представлена схема теплоперндачи через стенку кипятильный трубы первого корпуса. Здесь:  тепловой поток через поверхность теплообмена первого корпуса;
тепловой поток через поверхность теплообмена первого корпуса;  - коэффициент теплоотдачи от конденсирующегося пара первого корпуса к наружной поверхности кипятильной трубы;
- коэффициент теплоотдачи от конденсирующегося пара первого корпуса к наружной поверхности кипятильной трубы; 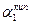 - коэффициент теплоотдачи от внутренней поверхности кипятильной трубы к кипящему раствору первого корпуса;
- коэффициент теплоотдачи от внутренней поверхности кипятильной трубы к кипящему раствору первого корпуса;  - коэффициент теплопроводности стенки кипятильной трубы;
- коэффициент теплопроводности стенки кипятильной трубы; 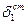 - толщина стенки кипятильной трубы;
- толщина стенки кипятильной трубы; 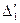 - составляющая полезной разности температур первого корпуса со стороны греющего пара;
- составляющая полезной разности температур первого корпуса со стороны греющего пара; 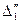 - составляющая полезной разности температур первого корпуса со стороны стенки;
- составляющая полезной разности температур первого корпуса со стороны стенки; 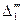 - составляющая полезной разности температур первого корпуса со стороны кипящего раствора.
- составляющая полезной разности температур первого корпуса со стороны кипящего раствора.
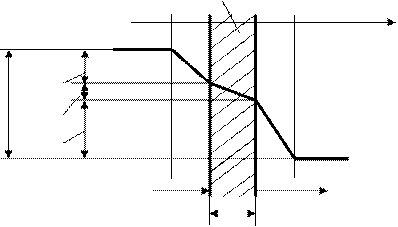


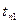
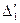
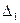
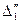
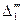
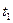
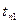

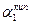
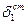
Рис.2.2. Схема теплопередачи через стенку кипятильный трубы первого корпуса от конденсирующегося пара к кипящему раствору.
Для стадии теплоотдачи от конденсирующегося пара к стенке поток теплоты Q1 выражается уравнением 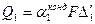 . где
. где 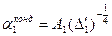 ; поэтому
; поэтому  . Откуда
. Откуда  (8.2)
(8.2)
Для стадии кондуктивного теплопереноса через стенку толщиной 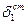 при коэффициенте теплопроводности
при коэффициенте теплопроводности  тот же поток теплоты Q1определяется выражением
тот же поток теплоты Q1определяется выражением 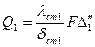 , откуда
, откуда  . (9.2)
. (9.2)
Для стадии теплоотдачи от стенки к кипящему раствору  , где
, где 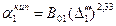 ; тогда
; тогда 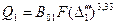 , откуда
, откуда  (10.2)
(10.2)
Складывая, левые и правые части уравнений (8.2), (9.2) и (10.2), получим выражение для полезной разности температур первого корпуса в виде
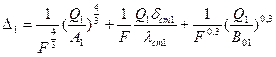 . (11.2)
. (11.2)
По аналогии запишем выражения для определения полезной разности температур второго и третьего корпусов
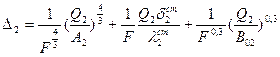 . (12.2)
. (12.2)
 . (13.2)
. (13.2)
Следовательно, полная полезная разность температур для МВУ с тремя корпусами будет равна
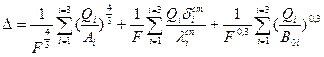 . (14.2)
. (14.2)
Полезная разность температур для МВУ с любым числом корпусов, n
 . (15.2)
. (15.2)
Для удобства решения этого уравнения относительно F умножим обе части уравнения на 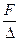 . В результате получим
. В результате получим
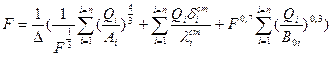 , (15.2)
, (15.2)
где 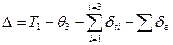 .
.
Полученное уравнение решается относительно F методом последовательных приближений.
Выше было показано, что с ростом числа корпусов МВУ суммарная полезная разность температур падает. При этом понижается разность температур приходящаяся на один корпус, а поверхность теплообмена возрастает. Последнее приводит к увеличению размеров и стоимости МВУ, а также затрат на ее обслуживание. Поэтому суммарный экономический эффект при росте числа корпусов становится менее ощутимым. Для обеспечения устойчивой работы МВУ принято считать, что минимальная разность температур в одном корпусе должна составлять 100С. По этой причине число корпусов МВУ составляем преимущественно 2 – 4, реже 5 – 6.
Примечание.
По условиям теплопередачи более выгодны МВУ с противоточным движением раствора и паров. Однако, существенным недостатком такой схемы является необходимость принудительного перемещения раствора из корпуса в корпус в сторону нарастающего давления, что требует применения насосов, работающих в жестких условиях. По этой причине в подавляющем большинстве случаев применяется прямоточная схема МВУ, рассмотренная выше.
| <== предыдущая лекция | | | следующая лекция ==> |
| Обозначения. | | | Выпарная установка с частичным тепловым насосом. Область использования. Коэффициент инжекции. |
Дата добавления: 2015-03-11; просмотров: 1116;