Перестановки. Определение. Комбинации из nэлементов множества, отличающиеся порядком, называются перестановками.
Определение. Комбинации из nэлементов множества, отличающиеся порядком, называются перестановками.
Число перестановок из n элементов обозначается Pn.
P n = n! (3.2)
Пример 3.3. Сколькими способами можно разместить на полке три книги?
В данной задаче необходимо найти число перестановок из четырех элементов. Существует четыре варианта выбора первой книги. Далее остается три варианта выбора второй книги, два варианта третьей книги и один способ выбора четвертой книги.
Таким образом, число способов N разместить четыре книги на полке равно произведению чисел 4, 3, 2 и 1, т. е.
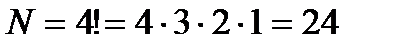 способа.
способа.
Пример 3.4.Сколько различных буквенных комбинаций можно составить из букв слова «апельсин»?
Слово «апельсин» состоит из 8 различных букв, поэтому число буквенных комбинаций равно числу перестановок из 8 элементов, то есть применима формула (3.2)
P8 = 8! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 = 40320 способов.
Интересно отметить, что из всех этих комбинаций только одна – спаниель – является осмысленным словом русского языка.
3.1. Сократить дробь:
а)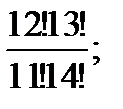 б)
б) 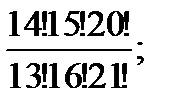 в)
в) 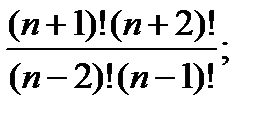 г)
г) 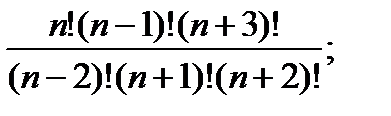 д)
д) 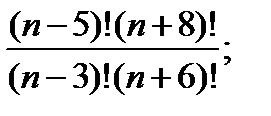 е)
е) 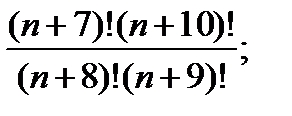 ж)
ж) 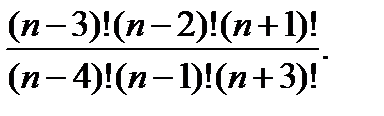
3.2. Сколько различных предложений можно составить из трех слов: «сегодня», «идет», «дождь»?
3.3. Сколько различных пятизначных чисел, в которых цифры не повторяются, можно составить из цифр: 1, 2, 3, 4 и 5?
3.4. Сколькими способами можно разместить четырех пассажиров в четырехместном купе поезда?
3.5. Порядок выступления семи участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Дата добавления: 2014-12-14; просмотров: 988;
