Пример 2.21. Исследовать на сходимость ряд:
Исследовать на сходимость ряд:
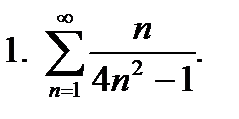
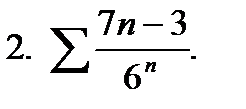
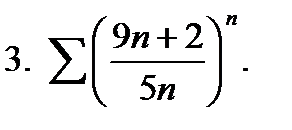
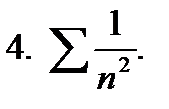
Решение.
1. 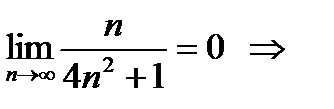 необходимо применить один из признаков сходимости положительных рядов – признак сравнения.
необходимо применить один из признаков сходимости положительных рядов – признак сравнения.
При 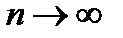
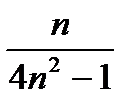 ~
~ 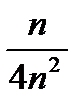 ~
~ 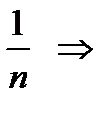 сравним исходный ряд с расходящимся рядом
сравним исходный ряд с расходящимся рядом 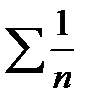 .
.
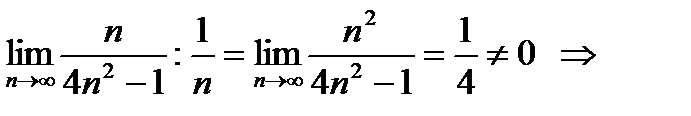 исходный ряд расходится.
исходный ряд расходится.
2. Применим признак Даламбера (найдем 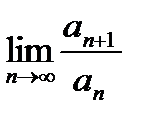 ):
):
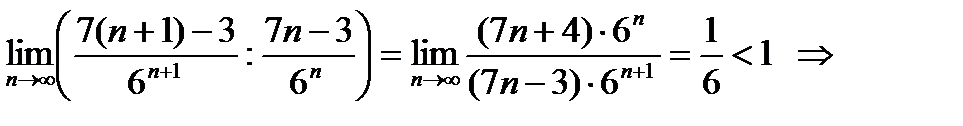 ряд сходится.
ряд сходится.
3. Применим радикальный признак Коши (найдем 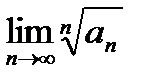 ):
):
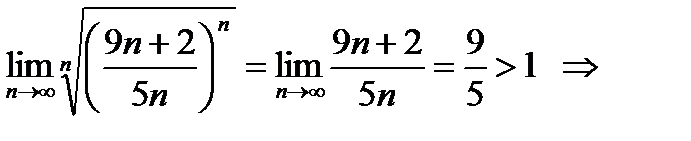 ряд расходится.
ряд расходится.
4. Применим интегральный признак Коши. Функция 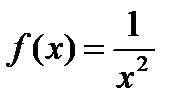 непрерывная, убывающая и положительная на промежутке [1; ∞).
непрерывная, убывающая и положительная на промежутке [1; ∞). 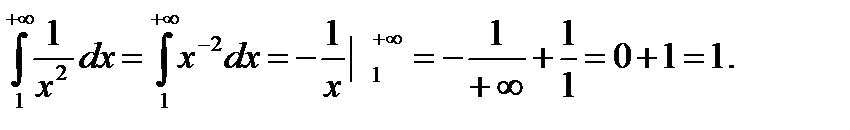
Интеграл сходится, следовательно, и ряд 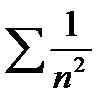 сходится.
сходится.
Замечание. С помощью интегрального признака Коши можно доказать, что ряд 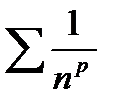 сходится при р > 1 и расходится при р ≤ 1.
сходится при р > 1 и расходится при р ≤ 1.
2.93. Исследовать ряд на сходимость:
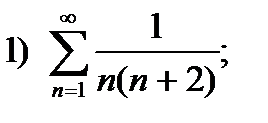 2)
2) 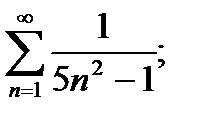 3)
3) 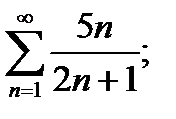
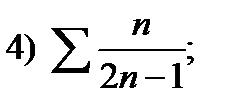
5) 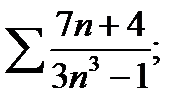 6)
6) 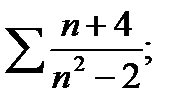 7)
7) 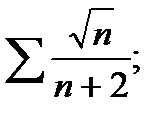 8)
8) 
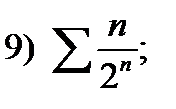
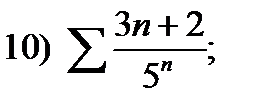
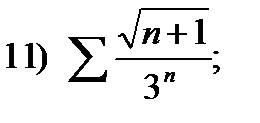
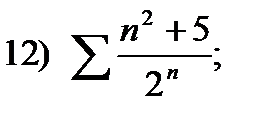
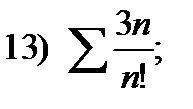
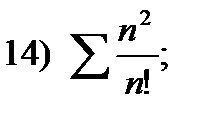
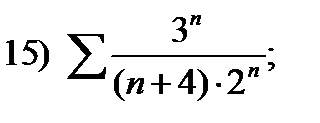
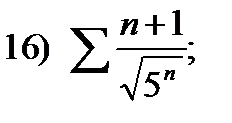
17) 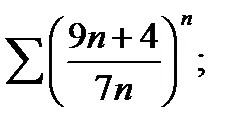 18)
18) 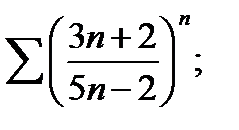 19)
19) 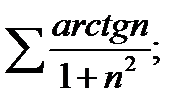 20)
20) 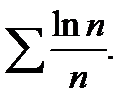
2.94. Исследовать на абсолютную и условную сходимость ряд:
1) 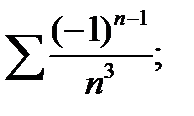 2)
2) 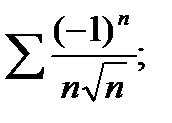 3)
3) 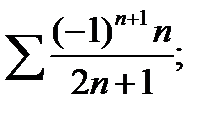 4)
4) 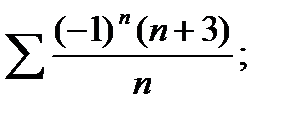 5)
5) 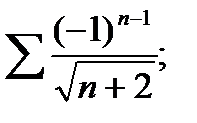
6) 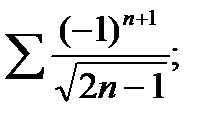 7)
7) 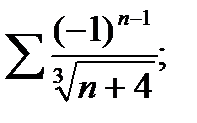 8)
8) 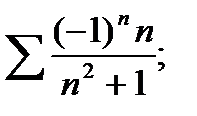 9)
9) 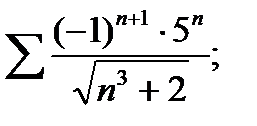 10)
10) 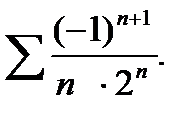
Дата добавления: 2014-12-14; просмотров: 1249;
