г.Москва 15-18 декабря 2014г. от Омской Области. Великий немецкий математик Карл Фридрих Гаусс, будучи гимназистом, обращал дроби вида 1/р, где р – простое число
2.1 Длина периода
Великий немецкий математик Карл Фридрих Гаусс, будучи гимназистом, обращал дроби вида 1/р, где р – простое число, отличное от 2 и 5, в бесконечные десятичные дроби: в каждом случае он с поразительным терпением ожидал, когда знаки начнут повторяться. Ему хотелось понять, как зависит длина периода такой дроби от р.
Мы в своей работе для вычисления длины периода использовали программу, написанную на языке Паскаль.
programdrobi;
vark,r,b:integer;
begin
write ('b='); readln(b);
k:=1;
r:=10;
while r <> 1 do
begin
r:=(10*r) mod b;
k:=k+1;
end;
write (k);
end.
И вот, что получилось.
р – знаменатель дроби (простое число, отличное от 2 и 5), L(p) – количество цифр в периоде.
| р | ||||||||||||||
| L(p) |
Т.о. из таблицы видно, что длина L(p) наименьшего периода для некоторых дробей совпадает с числом р – 1. А именно, L(p) = р – 1 для р = 7, 17, 19, 23, 47, 59, 61, 97, 109, 113 и т.д.. Конечно или бесконечно множество таких чисел по сей день неизвестно.
Также из таблицы видна еще одна закономерность: длина наименьшего периода является делителем числа р – 1
2.1 Эффект девятки
Рассмотрим записи обыкновенных дробей в виде периодических
| Обыкновенная дробь | Периодическая дробь |
| 1/7 | 0,(124857) |
| 2/7 | 0,(285714) |
| 3/7 | 0,(428571) |
| 4/7 | 0,(571428) |
| 5/7 | 0,(714285) |
| 6/7 | 0,(857142) |
| Обыкновенная дробь | Периодическая дробь | Обыкновенная дробь | Периодическая дробь |
| 1/11 | 0,(09) | 6/11 | 0,(54) |
| 2/11 | 0,(18) | 7/11 | 0,(63) |
| 3/11 | 0,(27) | 8/11 | 0,(72) |
| 4/11 | 0,(36) | 9/11 | 0,(81) |
| 5/11 | 0,(45) | 10/11 | 0,(90) |
| Обыкновенная дробь | Периодическая дробь | Обыкновенная дробь | Периодическая дробь |
| 1/13 | 0,(076923) | 7/13 | 0,(538461) |
| 2/13 | 0,(153846) | 8/13 | 0,(615384) |
| 3/13 | 0,(230769) | 9/13 | 0,(692307) |
| 4/13 | 0,(307692) | 10/13 | 0,(769230) |
| 5/13 | 0,(384615) | 11/13 | 0,(615384) |
| 6/13 | 0,(461538) | 12/13 | 0,(923076) |
Удивительно, но какую бы дробь мы не взяли, сумма цифр периода кратна девяти:
для дробей со знаменателем 7 эта сумма равна 27 = 9 × 3;
для дробей со знаменателем 11: 9 = 9 × 1;
для дробей со знаменателем 13: 27 = 9 × 3;
для дробей со знаменателем 19: 81 = 9 × 9;
для дробей со знаменателем 31: 54 = 9 × 6;
для дробей со знаменателем 37: 9 = 9 × 1 или 18 = 9 × 2 и т. д.
Докажем это свойство. Рассмотрим дробь вида  . При делении уголком числителя на знаменатель получаем:
. При делении уголком числителя на знаменатель получаем: 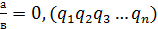 . Обозначим через r1, r2, r3 и т. д. rn – остатки, получаемые при делении. Тогда
. Обозначим через r1, r2, r3 и т. д. rn – остатки, получаемые при делении. Тогда
10a = bq1 + r1,
10r1 = bq2 + r2,
10r2 = bq3 + r3
……………….
10rn-1 = bqn + rn
Из полученных равенств выразим q1, q2, q3 и т.д. и найдем сумму этих чисел. Получим:
 ,
,
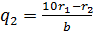 ,
,
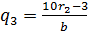 ,
,
……………..
 ,
,
q1 + q2 + q3 + … + qn = 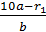 +
+ 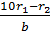 +
+  + …
+ … 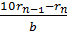 =
=
= 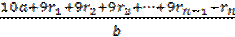 ( т.к. числа начинают повторяться, то
( т.к. числа начинают повторяться, то
a = rn) = 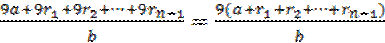 кратно 9.
кратно 9.
2.2 Циклические сдвиги
Рассмотрим следующие разложения:
1/7 = 0,(142857),
2/7 = 0,(285714),
3/7 = 0,(428571),
4/7 = 0,(571428),
5/7 = 0,(714285),
6/7 = 0,(857142).
Периоды этих шести дробей начинаются сразу же после запятой и получаются друг из друга циклическим сдвигом. Случайно ли это?
Возьмем вместо 7, например, 41.
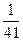 = 0,(02439).
= 0,(02439).
«Прокрутим» период: 0,(24390) = 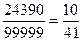 .
.
Полученная дробь в 10 раз больше первоначальной. Посмотрим, что получится, если мы полученную дробь снова умножим на 10 и вычтем целую часть.
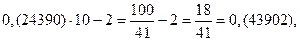
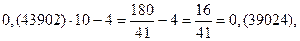

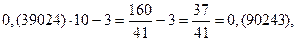
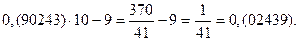
Получился замкнутый цикл из дробей, имеющих одинаковые цифры в периоде. Проведем аналогичные операции, взяв другую дробь.
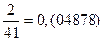
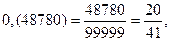
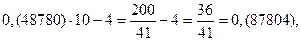
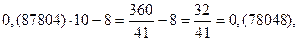
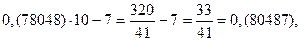
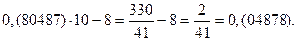
Снова получился замкнутый цикл из дробей с одинаковыми цифрами в периоде, причем, количество дробей в цикле одинаково.
Таким образом, можно предположить, что десятичные дроби образуют замкнутые циклы, в которые входят дроби, имеющие одинаковые цифры в периоде, причем каждую последующую дробь можно получить из предыдущей умножением на десять с последующим вычитанием целой части.
2.3 Особенности числителей дробей цикла
Рассмотрим некоторые циклы.
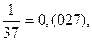
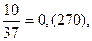
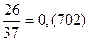
Заметим, что сумма числителей дробей равна знаменателю: 1 + 10 + 26 = 34.
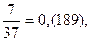
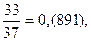
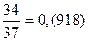
Заметим, что сумма числителей дробей равна удвоенному знаменателю: 7 + 33 + 34 = 74 = 37 × 2.
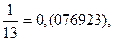

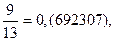
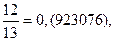


Заметим, что сумма числителей дробей равна утроенному знаменателю: 1 + 10 + 9 + 12 + 3 + 4 = 39 = 13 ×3.
Во всех случаях сумма числителей дробей, образующих цикл, кратна знаменателю. Проанализировав, полученные нами данные, мы заметили следующую закономерность: сумма числителей дробей цикла во столько раз больше знаменателя дроби, во сколько раз сумма цифр периода больше 9.
г.Москва 15-18 декабря 2014г. от Омской Области
| № | ФИО | Год рождения | Спортивный разряд | Паспортные данные | ФИО тренера | Виза, печать и подпись врача напротив каждой фамилии |
| Костякова Наталья | МС | 5209 785827 | Мартынов В.А. | |||
| Мартынова Ольга | КМС | 5214 371399 | Мартынов В.А. | |||
| Хомова Екатерина | КМС | 5208 671085 | Мартынов В.А. | |||
| Жайлибаев Кайнар | КМС | 5208 740733 | Мартынов В.А. | |||
| Киселев Илья | МС | 5209 862316 | Мартынов В.А. | |||
| Курдяев Сергей | III р | I-KH № 502161 | Мартынов В.А. | |||
| Гудалова Варвара | II р | Мартынова О.А | ||||
| Бычков Никита Толстокоренко Евгений | II р II р | 1-КН №600206 1-КН №557367 | Мартынова О.А Мартынова О.А | |||
| Перешивка Влад | II р | 1-КН №559986 | Мартынова О.А | |||
| Ефремова Анжелика | II р | I-КН № 677462 | Мартынова О.А | |||
| Назарова Валя | II р | Мартынова О.А | ||||
| Нерсисян Арман | II р | I- КН № 624704 | Галиуллина О.А | |||
| Герасимов Леонид | II р | I- КН № 673612 | Галиуллина О.А | |||
| Саргсян Карен | II р | АА № 340173 | Галиуллина О.А | |||
| Шпринц Кристина | II р | I-ЛО №746152 | Костякова Н.А. | |||
| Белкина Екатерина | II р | I- КН № 559499 | Мартынова О.А | |||
| Всего допущено: Официальным представителем команды является: Мартынов В. А. |
| <== предыдущая лекция | | | следующая лекция ==> |
| | | г.Москва 15-18 декабря 2014г. от Омской Области |
Дата добавления: 2014-11-30; просмотров: 1247;
