Оптимальное построение кольцевых маршрутов
Исходной информацией для решения задачи являются условные схемы размещения пунктов, которые должны быть включены в маршрут, и матрица расстояний C = (cij) между этими пунктами, (см. табл. 4.1) в километрах. Рассмотрим решение задачи построения кольцевого маршрута на примере. Исходными данными для примера будут данные табл.4.1.
Алгоритм решения состоит из нескольких шагов.
Таблица 4.1
| Пункт отправления i | Пункт назначения j | ||||
Шаг 1. Исходную матрицу (треугольная матрица (табл. 4.1)) заполним так, чтобы матрица стала симметричной по отношению к главной диагонали (табл.4.2).
Таблица 4.2
| Пункт отправления i | Пункт назначения j | min | ||||
Шаг 2. Получение приведенной матрицы.
Приведенной будем называть такую матрицу, которая имеет хотя бы один нулевой элемент. Для получения приведенной матрицы в каждой строке находим минимальный элемент и выписываем его с правой стороны матрицы. Это вектор-столбец вида (3, 3, 6, 5, 4) (см. табл.4.1). Из элементов соответствующей строки вычитаем минимальное значение элемента этой строки и получаем приведенную матрицу по строкам (см. табл. 4.3).
Таблица 4.3
| Пункт отправления i | Пункт назначения j | ||||
| min |
Затем в каждом столбце находим минимальный элемент и выписываем их внизу матрицы. Это вектор-строка вида (0, 0, 2, 2, 0) (см. табл.4.3). Из элементов соответствующего столбца вычитается минимальное значение элемента этого столбца, и получают приведенную матрицу (табл.4.4). Математически доказано, что сделанные описанным способом процедуры получения приведенной матрицы (табл. 4.4) сохраняют свойства исходной матрицы.
Элемент приведенной матрицы cij будем называть полюсом, если cij = 0.
Таблица 4.4
| Пункт отправления i | Пункт назначения j | ||||
Шаг 3. Последовательно для каждого полюса выполним следующее:
- для строки i0, где находится полюс, находим минимальный элемент этой строки, исключая значение только для самого этого полюса:
- для столбца j0, где находится полюс, находим минимальный элемент этого столбца, исключая значение только для самого этого полюса.
Находим значение параметра d( i0, j0) по формуле
d( i0, j0) = min ( cij) + min( cij ).
Имеем:
d12 = 1 + 0 = 1,
d21 = 0 + 0 = 0,
d24 = 0 + 2 = 2,
d35 = 2 + 1 = 3,
d42 = 2 + 0 = 2,
d51 = 0 + 0 = 0,
d53 = 0 + 3 = 3.
Шаг 4. Находим параметр h(i0,j0) по формуле
h(i0,j0) = max ( dij ).
Если таких значений будет несколько, можно выбрать любое. Выбранный параметр h(i0,j0) показывает направление движения: нужно двигаться из пункта i0 в пункт j0. Чтобы не было возврата, делаем запрет, полагая c(j0,i0) = \\\\.
В нашем примере имеем
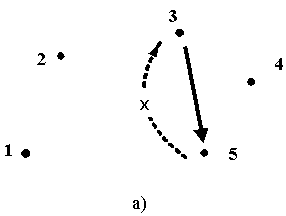
h35 = 3 и h53 = 3. Возьмем первый случай: h(i0,j0) = h35 . Так как i0 = 3, а j0 = 5, то будем двигаться из пункта 3 в пункт 5 (см. рис. 4.1а.). В этом случае запрет будет иметь вид с53=\\\\.
Шаг 5. Вычеркиваем строку i0 и столбец j0, сохраняя номера строк и столбцов матрицы неизменными. Для нашего примера это будет матрица табл. 4.5.
Таблица 4.5
| Пункт | Пункт назначения j | |||
| отправления i | ||||
| \\\ |
Шаг 6. Если после вычеркивания в полученной матрице нет ни одного полюса, то необходимо создать полюса, применяя процедуры, описанные для шага 2. Получив приведенную матрицу, в которой имеются полюса, переходим к шагу 3.
Если после вычеркивания получаем матрицу (2Х2), то эту матрицу будем называть тривиальной, так как она позволяет однозначно достроить маршрут до кольцевого маршрута и получить решение задачи.
Рассмотрим последовательность действий для нашего примера.
Таблица 4.6
| Пункт | Пункт назначения j | |||
| отправления i | ||||
| \\\\ |
Так как в табл. 4.6 имеются полюса, то для каждого полюса находим d-параметры:
d12= 2 + 0 = 2,
d21= 0 + 0 = 0,
d24= 0 + 2 = 2,
d42= 2 + 0 = 2,
d51= 3 + 0 = 3.
Находим h-параметр. Получим:
h(i0,j0) = d51 = 3.
Вычеркиваются строка i0 = 5 и столбец j0 = 1 и полагаем элемент c15=\\\\ (в нашем случае этот элемент отсутствует). Проводим стрелку от пункта 5 к пункту 1, согласно процедуре шага 4 (см. рис. 4.1б.). Однако чтобы избежать зацикливания 3 - 5 - 1 - 3, полагаем с13=\\\\.
После этого составляется новая матрица (табл. 4.7).
Таблица 4.7
| Пункт | Пункт назначения j | ||
| отправления i | |||
| \\\\ | |||
Так как в табл. 4.7 имеются полюса, снова рассчитываем d- и h-параметры. Получим:
d12 = 2 + 0 = 2,
d24 = 3 + 2 = 5,
d42 = 3 + 0 = 3.
Анализ полученных значений дает
h(i0,j0) = d24 = 5.
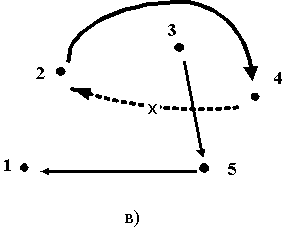
Организуем перевозку из пункта 2 в пункт 4 (см. рис. 4.1в.). Вычеркивается строка i0 = 2 и столбец j0 = 4. Чтобы избежать зацикливания, полагаем с42=\\\\. Получаем матрицу табл. 4.8.
Таблица 4.8
| Пункт | Пункт назначения j | |
| отправления i | ||
| \\\\ | ||
| \\\\ |
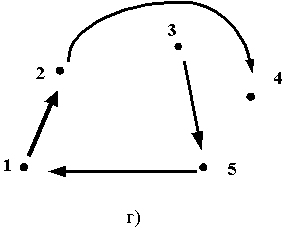
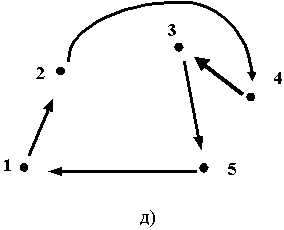
Получена тривиальная матрица (2х2). По значениям этой матрицы строим две связи: 1 – 2 (т. к. по табл. 4.8 «расстояние» между этими пунктами самое короткое) и 4 – 3, чтобы получить замкнутый циклический маршрут (рис. 4.1г. и 4.1д. соответственно).
Протяженность кольцевого маршрута составляет 28 км. Это можно проверить по исходным данным табл. 4.1, обходя по контуру маршрута, начиная с пункта 3:
L = 6 + 4 + 3 + 5 + 10 = 28 (км).
| 
|
| 
|
|
Рис. 4.1. Результаты конструирования маршрута (по шагам)
Заключение
Решению текущих, практических задач многие предприятия и организации уделяют в последнее время все больше и больше внимания. Результатом этой работы является снижение затрат или снижение темпов роста затрат по сравнению с результатами прошлых лет. Значительно больше внимания уделяется опыту организации логистических операций зарубежных фирм. По мнению экспертов из Великобритании, средний размер торгового рынка Европы к 2003 г. составлял 800 млрд. дол. Следовательно, без эффективного и гибкого логистического сервиса многие предприятия РФ просто не будут допущены к этому исключительно привлекательному рынку. Это означает, что для всех без исключения предприятий и организаций задачи логистики должны обязательно включаться в список задач по управлению ими.
Данное учебное пособие дает возможность будущему экономисту получить первые сведения об особенностях организации логистических звеньев и систем, о характере задач, обеспечивающих эффективный логистический сервис и позволяющих дополнительно сдерживать рост затрат. В пособии сделана попытка большее внимание уделить практической стороне в решении конкретных задач. Наряду с хорошо зарекомендовавшими схемами, предлагается новый алгоритм организации транспортных перевозок в виде конструирования циклических маршрутов. Имея в виду, что задачи организации перевозок, позволяющие получить минимум затрат или минимум другого экономического показателя (время, побег и др.), относятся к классу комбинаторных задач, предлагаемый алгоритм позволяет достаточно просто решать практические задачи средней размерности (примерно до 30 – 40 пунктов).
Дата добавления: 2014-11-30; просмотров: 1796;
