Понятие о квантовой теории электропроводности металлов

Согласно квантовой теории электроны проводимости металла образуют не классический газ, а вырожденный электронный газ, подчиняющийся квантовой статистике Ферми-Дирака. Теплоемкость такого газа составляет всего 0.01R. Поэтому при обычных температурах теплоемкость металла равна практически теплоемкости решетки (3R).

Квантово-механический расчет электропроводности металлов провел Зоммерфельд. Для проводимости он получил следующую формулу:

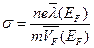, (3)

где 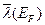- средняя длина свободного пробега электронов, обладающих энергией Ферми. 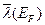- относится не ко всем электронам, а только к тем, которые расположены на поверхности Ферми. 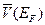- средняя скорость электронов на поверхности Ферми. Согласно классической теории в формулу для электропроводности входит средняя скорость теплового движения электронов 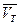при данной температуре. В отличие от 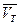, скорость 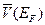практически не зависит от температуры.

Согласно классической электронной теории сопротивление электрическому току в металлах обусловлено непрерывным столкновением электронов с узлами кристаллической решетки. Квантовая теория рассматривает электрон как частицу, обладающую волновыми свойствами. Движение электронов проводимости в металле рассматривается как процесс распространения электронных волн. Длина этих волн определяется соотношением де Бройль

.

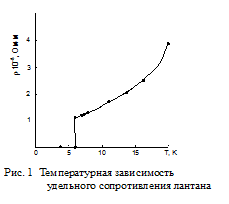
Согласно квантовой теории идеальная кристаллическая решетка, в узлах которой находятся неподвижные атомы, не рассеивает электронные волны и не оказывает сопротивления движению электронов. Рассеивание электронов возникает лишь с появлением в решетке центров рассеивания – неоднородностей, по размерам превосходящих длину электронных волн. Такими центрами могут быть искажения решетки, обусловленные тепловыми колебаниями атомов. Тепловые колебания приводят к возникновению микрообъемов, в которых плотность выше средней плотности вещества, либо ниже средней плотности вещества. Вследствие этого плотность твердого тела меняется при переходе от одного микрообъема к другому. Размеры таких микрообъемов превышают длину электронных волн. Поэтому они являются центрами рассеяния электронных волн.

Согласно квантовой теории ,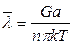

где n - число атомов в 1м²; G - модуль упругости; а - параметр решетки.

Тогда 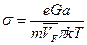. (4)

Таким образом , что хорошо согласуется с экспериментальными данными.

Кроме тепловых колебаний решетки источником рассеяния электронных волн являются примесные атомы. Атомы примеси искажают решетку основного металла и действуют как рассеивающие центры. Поэтому при наличии примесей коэффициент рассеяния складывается из коэффициента рассеяния, обусловленного тепловыми колебаниями атомов η_Т, и коэффициента рассеяния, определяемого примесями η_П:

η = η_Т + η_П.

При не слишком низких температурах выполняется соотношение η_Т ~ T. Величина η_П – пропорциональна концентрации примесей и не зависит от температуры.

Аналогично, для удельного сопротивления выполняется соотношение:

,

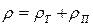где ρ_Т – сопротивление, обусловленное рассеянием электронов на тепловых колебаниях решетки; ρ_П – сопротивление, обусловленное рассеянием электронов на атомах примеси.