Классическая теория электропроводности металлов

Классическая электронная теория металлов развита Друде, Томсоном и Лоренцем. Согласно этой теории электронный газ в металле рассматривается как идеальный газ, и к нему применяют законы классической механики и статистики. В отсутствие внешнего электрического поля свободные электроны в металле совершают хаотическое тепловое движение, не создающее направленного переноса электрического заряда. При наложении электрического поля Е на каждый электрон действует сила

F = - eE,

направленная против поля и приводящая к возникновению электрического тока. Движение электрона в кристалле представляет собой сложное движение вследствие постоянного его столкновения с ионами в узлах кристаллической решетки. Между двумя актами столкновения электрон ускоряется. В конце длины свободного пробега λ под действием силы F электрон приобретает скорость направленного движения

,

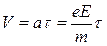где m – масса электрона; а - его ускорение; τ – время движения электрона между двумя столкновениями. τ называется временем свободного пробега. В результате столкновения с ионом скорость электрона обращается в нуль. Поэтому средняя скорость упорядоченного движения равна:

.

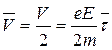Так как ,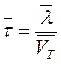

то ,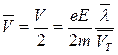

где 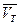- средняя скорость теплового движения электронов.

Величина 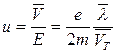называется подвижностью. Подвижность равна скорости, приобретаемой электроном в электрическом поле, напряженность которого равна Е=1 В/м.

В электрическом токе движение электрона является сложным движением, представляющим собой наложение хаотического теплового движения с упорядоченным движением со скоростью 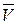в электрическом поле. Электрическое сопротивление металла обусловлено столкновением электронов с узлами кристаллической решетки и выходом их из общего потока. Чем чаще электрон сталкивается с узлами, тем выше электрическое сопротивление металла.

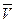При средней скорости упорядоченного движения через площадку в 1 м² , расположенную перпендикулярно к потоку, за 1 секунду пройдут все электроны, заключенные в параллелепипеде с ребром . Объем этого параллелепипеда равен 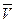, число электронов в нем - 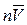, n – концентрация электронов в металле. Эти электроны перенесут заряд, равный 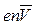. Тогда плотность тока в проводнике будет равна

.

Для удельной проводимости имеем

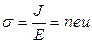. (1)

Подставляя в формулу (1) значение u для проводимости металла получим выражение:

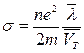. (2)

Таким образом, согласно классической теории проводимость металла определяется средней длиной свободного пробега электрона в кристалле и средней скоростью теплового движения. Средняя длина свободного пробега равна примерно межатомному расстоянию в решетке. Для выяснения справедливости такого предположения, оценим величину для серебра используя экспериментальные данные по проводимости. Среднюю скорость теплового движения электронов определим из соотношения:

.

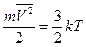Тогда для температуры Т~300 K получим 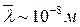. Эта величина на два порядка больше, чем межатомное расстояние для серебра. Следовательно, экспериментальные значения проводимости металлов могут быть объяснены, если предположить, что длина свободного пробега электрона намного превышает среднее расстояние между атомами. При своем движении электрон не так часто сталкивается с ионами в узлах кристаллической решетки, как предполагает классическая теория. Прежде чем испытать столкновение электрон пролетает достаточно большое расстояние, равное, примерно 100 межатомным расстояниям в кристалле. Этот факт классическая теория не в состоянии объяснить.

Следующее затруднение классической теории сводится к температурной зависимости электросопротивления. Согласно классической теории средняя длина свободного пробега не зависит от температуры и равна среднему межатомному расстоянию в кристалле. Поэтому, согласно формуле (2) температурная зависимость сопротивления определяется температурной зависимостью скорости теплового движения . Тогда удельное сопротивление согласно классической теории определяется выражением 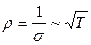. Однако, экспериментальные данные показывают, что для металлов сопротивление в широком интервале растет линейно с ростом температуры .

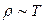Перечисленные трудности классической теории электропроводности свидетельствуют о том, что основное допущение этой теории – рассмотрение свободных электронов металла как частиц идеального газа, подчиняющихся статистике Максвелла-Больцмана, является неправильным.

Контрольные вопросы

1. Основные положения классической теории электропроводности металлов. Какими параметрами определяется проводимость металла согласно классической теории?
2. С какими затруднениями сталкивается классическая теория при объяснении экспериментальных фактов?
3. Что называется подвижностью?

4. В чем состоит механизм электрического сопротивления согласно классической теории?