Знаходження корінь рівняння
Як приклад візьмемо рівняння: x3 – 0,01x2 – 0,7044x + 0,139104 = 0
Тому що дане рівняння є поліномом третього ступеня, то для нього є не більше трьох речовинних корíнь. Для знаходження корíнь спочатку потрібно знайти інтервали, на яких ці корені існують. Такими інтервалами локалізації можуть служити проміжки, на кінцях яких функція має протилежний знак. З метою знаходження інтервалів, на кінцях яких функція змінює знак, необхідно побудувати її (тобто протабулювати). Протабулюємо рівняння на інтервалі [-1; 1] із кроком 0,2. Для цього:
1. Введіть в комірку А2 значення -1, а в комірку А3 - значення -0,8.
2. Виберіть діапазон А2:А3, розташуєте покажчик миші на маркері заповнення цього діапазону й простягніть його на діапазон А4:А12. Аргумент буде протабульовано.
3. В комірку В2 введіть формулу:
=A2^3-0,01*A2^2-0,7044*A2+0,139104
4. Виберіть комірку В2. Розташуєте покажчик миші на маркері заповнення цієї комірки та простягніть його на діапазон B3:B12. Функція також протабулюється.
З розрахунків видно, що поліном змінює знак на інтервалах [-1; -0,8], [0,2; 0,4] й [0,6; 0,8], тому на кожному з інтервалів є свій кóрінь; тому що поліном третього ступеня має не більше трьох корíнь, то таким чином вони всі локалізовані.
Перш ніж приступити до знаходження корíнь за допомогою підбора параметра, необхідно виконати підготовчі операції:
- Установіть точність, з якою находиться корінь. Корінь за допомогою підбора параметра находиться методом послідовних наближень. Виберіть команду Сервис -> Параметры й на вкладці Вычисления діалогового вікна Параметры задайте відносну погрішність і граничне число ітерацій рівними 0,00001 й 1000, відповідно.
- Відведіть на листі комірку, наприклад С2, під шуканий корінь. До застосування підбора параметра в ній знаходиться початкове наближення до кореня рівняння, а після застосування - знайдене значення кореня.
- В комірку С2 треба ввести значення, що є наближенням до шуканого кореня. У цьому випадку, першим відрізком локалізації кореня є [-1; -0.8], отже, за початкове наближення до кореня розумно взяти середню точку цього відрізка -0,9.
- Відведіть комірку, наприклад D2, під функцію, для якої ведеться пошук кореня, причому замість невідомої (y) цієї функції повинне вказуватися посилання на комірку, відведену під шуканий корінь. Таким чином, у комірку D2 введіть формулу:
=C2^3-0,01*C2^2-0,7044*C2+0,139104
Аналогічно робимо із двома іншими шуканими коріннями:
- Відвести комірку C3 під другий корінь, ввести в неї початкове наближення 0,3, а в комірку D3 ввести наступну формулу:
= C3^3-0,01*C3^2-0,7044*C3+0,139104
- Відвести комірку C4 під третій корінь, ввести в неї початкове наближення 0,7, а в комірку D4 ввести наступну формулу:
= C4^3-0,01*C4^2-0,7044*C4+0,139104
Тепер переходимо до знаходження першого кореня рівняння:
1. Виберіть команду Сервис -> Подбор параметра.
2. У поле Установить в ячейке введіть посилання на комірку D2 (мал. 4.7). У цьому полі дається посилання на комірку, у якій введена формула, що обчислює значення лівої частини рівняння. Для знаходження кореня за допомогою підбора параметра його необхідно представити в такому виді, щоб його права частина не містила змінну (уводити посилання на комірки в поля діалогового вікна Подбор параметра зручніше вибором відповідної комірки на листі, при цьому MS Excel автоматично буде перетворювати їх в абсолютні посилання).
3. У поле Значение введіть 0. Тут вказується значення із правої частини рівняння.
4. У поле Изменяя значение ячейки введіть С2. У даному полі приводиться посилання на комірку, відведену під змінну.
5. Натисніть кнопку ОК.
На екрані відобразиться вікно Результат подбора параметра з результатами роботи. Наближене значення кореня поміщене в комірку С2. У цьому випадку воно дорівнює -0,919999. Для наочності одержання нуля в комірці D2 варто встановити в ній числовий формат з 4 десятковими знаками. Аналогічно знаходимо два інші корені, вони рівні 0,21000 й 0,71999.
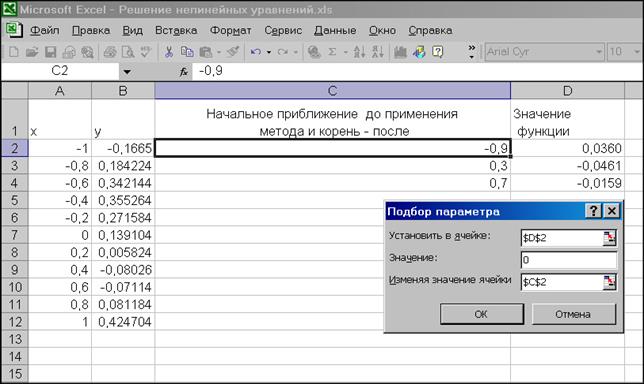
Мал. 4.7. Локалізація корíнь полінома
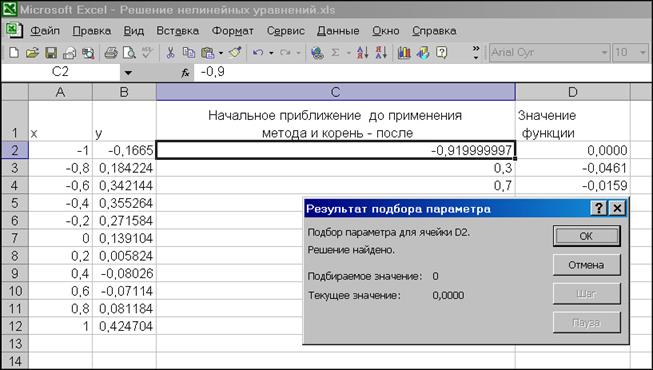
Мал. 4.8. Діалогове вікно результату підбора параметра
ПРАКТИЧНЕ ЗАВДАННЯ.
4.1.Побудувати графік функції відповідно до варіанта:
Варіант 1: sin(x)e-2x; при х Î[-2; 2];
Варіант 2: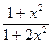 
; при х Î[-2; 2];
Варіант 3: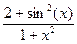 
; при х Î[-2; 1.5];
Варіант 4: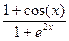 
; при х Î[-1.5; 1.5];
Варіант 5: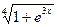 
; при х Î[-1.8; 1.8];
Варіант 6: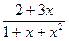 
; при х Î[-2; 1.8];
Варіант 7: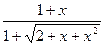 
; при х Î[-1.7; 1.5];
Варіант 8: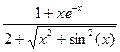 
; при х Î[-1.5; 1.8];
Варіант 9: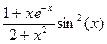 
; при х Î[-1.4; 1.9];
Варіант 10: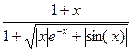 
; при х Î[-1.4; 1.4].
Крок функції вибрати самостійно.
4.2. Побудувати графік функції відповідно до варіанта:
Варіант 1: g=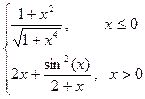 
; при х Î[-2; 2];
Варіант 2: g=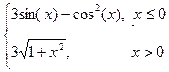 
; при х Î[-2; 2];
Варіант 3: g=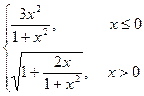 
; при х Î[-2; 1.5];
Варіант 4: g=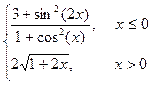 
; при х Î[-1.5; 1.5];
Варіант 5: g=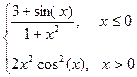 
; при х Î[-1.8; 1.8];
Варіант 6: g=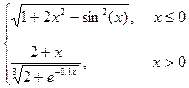 
; при х Î[-2; 1.8];
Варіант 7: g=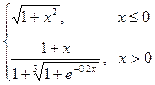 
; при х Î[-1.7; 1.5];
Варіант 8: g=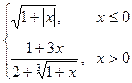 
; при х Î[-1.5; 1.8];
Варіант 9: g=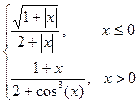 
; при х Î[-1.4; 1.9];
Варіант 10: g=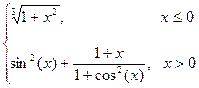 
; при х Î[-1.4; 1.4].
Крок функції вибрати самостійно.
4.3. Знайти всі корені рівняння:
Варіант 1: x3 + 1,41x2 - 5,4724x - 7,380384 = 0
Варіант 2: x3 + 0,85x2 - 0,4317x + 0,043911 = 0
Варіант 3: x3 - 2,92x2 + 1,4355x + 0,791136 = 0
Варіант 4: x3 - 2,56x2 - 1,3251x + 4,395006 = 0
Варіант 5: x3 + 2,84x2 - 5,6064x - 14,766366 = 0
Варіант 6: x3 - 0,12x2 - 1,4775x + 0,191906 = 0
Варіант 7: x3 + 0,77x2 - 0,2513x + 0,016995 = 0
Варіант 8: x3 + 0,88x2 - 0,3999x + 0,037638 = 0
Варіант 9: x3 + 0,78x2 - 0,8269x + 0,146718 = 0
Варіант 10: x3 + 2,28x2 - 1,9347x - 3,907574 = 0
Дата добавления: 2014-12-10; просмотров: 1605;