Позиционные системы счисления. Система счисления называется позиционной,если количественный эквивалент каждой цифры определяется не только видом символа
Система счисления называется позиционной,если количественный эквивалент каждой цифры определяется не только видом символа, ее изображающего, но и ее положением в записи числа. При этом место цифры в записи числаназывается разрядом.
Классическим примером позиционной системы счисления является десятичная система счисления.
В таблице 1 приведены примеры некоторых, наиболее часто употребляемых, позиционных систем счисления.
Таблица 1
| Основание | Система счисления | Знаки |
| Двоичная Восьмеричная Десятичная Шестнадцатеричная | 0, 1 0, 1, 2, 3, 4, 5, 6, 7 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F |
Одним из основных понятий в позиционных системах счисления являетсявес разряда. Весом j-го разряда для позиционной системы счисления называется отношение количественного эквивалента цифры xi, стоящей в j-м разряде, к количественному эквиваленту той же цифры, стоящей в нулевом разряде:
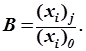
Число, указывающее сколько единиц младшего разряда содержится в единице старшего разряда,называетсяоснованием позиционной системы счисления.
Существует связь между основанием системы счисления и числом цифр, используемых в системе счисления (это видно из таблицы 1): для представления любого числа конечным числом разрядов в системе счисления с основанием K достаточно иметь K цифр. Обычно эти Kцифр составляют отрезок натурального ряда целых положительных чисел, включая 0. Таким образом, алфавит K-ичной системы счисления имеет вид {0, 1, 2, ..., K-1}.
Любое число Х в К-ичной позиционной системе счисления можно представить в виде полинома от основания К:
Х(К) = xn-1Kn-1 + xn-2Kn-2 + … + x1K + x0K0 + x-1K-1 + x-2K-2 + … + x-mK-m =
= 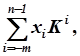 (1)
(1)
где xi – значение цифры в i – ом разряде;
Ki – основание системы счисления;
n,m – число разрядов в целой и дробной части числа, соответственно;
i – порядковый номер разряда.
Основание системы счисления обычно указывают (при необходимости) в виде десятичного индекса справа в нижней части числа.
Примеры:
23,43 (10) = 2×101 + 3×100 + 4×10-1 + 3×10-2
(в данном примере знак «3» в одном случае означает число единиц, а в другом - число сотых долей единицы);
451,2 (8) = 4×82 + 5×81 + 1×80 + 2×8-1.
Краткая запись числа представляется последовательностью цифр, каждой из которых можно поставить в соответствие определенную позицию. Обычно позиции, предназначенные для представления целой части числа, отделяют от позиций, предназначенных для представления дробной части числа – запятой:
Х(К) = xn-1 xn-2 … x1 x0, x-1 x-2 … x-m.
Запятая сама позиции не занимает, а является началом отсчета номера позиции: все позиции влево от запятой, предназначенные для хранения целой части числа, нумеруются в порядке возрастания натурального ряда чисел 0, 1, 2, ..., п-1, а все позиции вправо от запятой, предназначенные для хранения дробной части числа, нумеруются целыми отрицательными числами - 1, - 2, ...., - т. Таким образом, позиция цифры с присвоенным ей номером называетсяразрядомчисла.
На рисунке 1 показана нумерация разрядов в разрядной сетке ЭВМ, включающей п разрядов для представления целой и т разрядов – для представления дробной части числа. Под разрядной сеткой ЭВМпонимают общеечисло разрядов, отводимое для представления как целой, так и дробной части числа в цифровой вычислительной машине.
| n - 1 | n - 2 | … | -1 | -2 | … | -m |
Рисунок 1- Нумерация разрядов в разрядной сетке ЭВМ
Дата добавления: 2014-12-09; просмотров: 1582;
