Элементы погруженного объема судна при посадке его прямо и на ровный киль
3.4.1. Общие сведения.В расчетах плавучести, остойчивости и
других эксплуатационных свойств судна используются элементы погруженного объема корпуса, а именно:
- площадь ватерлинии S, координаты геометрического центра площади ватерлинии xf, yf , моменты инерции площади ватерлинии относительно продольной и поперечной центральных осей Jxf; Jyf;
- погруженная площадь шпангоута ω и координаты геометрического центра этой площади yω, zω;
- погруженный объем V и координаты геометрического центра этого объема, называемого центром величины (ЦВ) - xс, yс, zc;
Центральными - называются оси, проходящие через геометри-
ческий центр.
Все эти элементы зависят от посадки судна и в общем случае
являются функциями всех трех ее параметров - средней осадки d, угла крена Θи угла дифферента Ψ. В нормальных условиях судно плавает без крена. При этом, ввиду симметрии корпуса относительно ДП yf = 0, Jxf = Jx (здесь Jx - момент инерции площади S относительно следа ДП на данной ватерлинии), yω = 0 и yс = 0, а остальные элементы погруженного объема зависят в основном от двух параметров - d и Ψ. Рассмотрим элементы погруженного объема для наиболее простого случая посадки судна прямо и на ровный киль, когда они зависят только от одного параметра - средней осадки d.
3.4.2. Элементы площади ватерлинии. Величины S, xf , Jx и Jyf могут быть определены с помощью проекций теоретического чертежа.
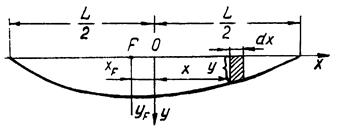
Рис.15. К определению элементов
площади ватерлинии
Для каждой теоретической ватерлинии (рис.15):
- площадь ватерлинии: 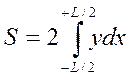 ;
;
- абсцисса геометрического центра тяжести площади S:
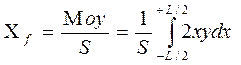 ,
,
где Мoy - статический момент площади S относительно следа плоскости мидель - шпангоута на плоскость данной ватерлинии;
- момент инерции площади S относительно следа ДП на плоскость данной ватерлинии:
 ;
;
- момент инерции площади S относительно следа плоскости мидель- шпангоута на плоскость данной ватерлинии:
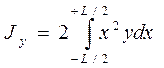 ;
;
- центральные моменты инерции площади S:
Jxf = Jx,
Jyf = Jy – S xf 2.
В этих выражениях – L/2 и + L/2 измеряются в плоскости соответствующей ватерлинии.
По результатам расчетов, выполненных для всех теоретических ватерлиний, могут быть построены кривые изменения элементов площади ватерлинии с изменением осадки S(d), xf(d), Jx(d) и Jyf (d) (рис.16).
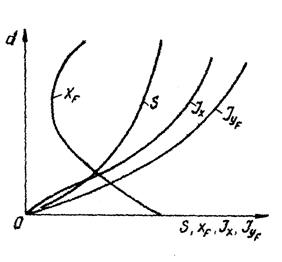
Рис.16. Кривые изменения
площади ватерлинии элементов
площади ватерлинии
3.4.3.Элементы погруженной площади шпангоута. Величины определяются с помощью проекций «корпус» теоретического чертежа.
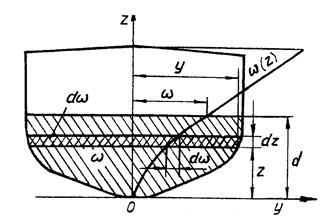
Рис.17. К определению элементов
погруженной площади
Для каждого теоретического шпангоута при плавании судна по заданную ватерлинию (рис.17):
- погруженная площадь шпангоута:
 ;
;
- аппликата геометрического центра площади ω:
zω 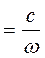
где 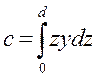 - статический момент площади ω относительно следа плоскости шпангоута на ОП.
- статический момент площади ω относительно следа плоскости шпангоута на ОП.
По результатам расчетов, выполненных для каждого теоретического шпангоута при осадках, соответствующих всем теоретическим ватерлиниям, могут быть построены кривые изменения элементов погруженной площади шпангоута с изменением осадки - ω(d) и zω(d). На основании этих расчетов для осадок судна по каждую теоретическую ватерлинию можно построить также кривые изменения элементов погруженной площади шпангоута по длине судна ω(x) и zω (x). Кривая ω(x) (рис.18) называется строевой по шпангоутам. Ее ординаты в масштабе представляют площади соответствующих шпангоутов. Каждой осадке отвечает своя строевая по шпангоутам.
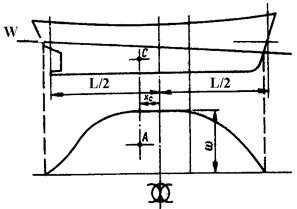
Рис.18. Строевая по шпангоутам
3.4.4. Элементы погруженного объема.Величины V, хс и zc могут быть определены с помощью строевой по ватерлиниям S(d), или строевой по шпангоутам ω(x).
Рассмотрим использование для этой цели строевой по ватерлиниям (см. рис. 16). Площадь, ограниченная строевой по ватерлиниям,
осью и следом ватерлинии, определяет собой величину погруженного по эту ватерлинию объема (объемного водоизмещения):

Аппликата геометрического центра объема V (аппликата ЦВ):
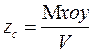
где: 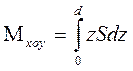 - статический момент объема V относительно плоскости x0y (ОП).
- статический момент объема V относительно плоскости x0y (ОП).
Рассмотрим использование строевой по шпангоутам (см. рис.18). Площадь ограниченная строевой по шпангоутам и осью x, определяет собой величину объема V по ватерлинию, которой соответствует эта строевая:
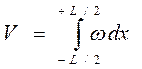
Абсцисса ЦВ:
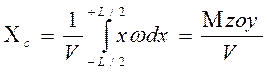 ,
,
где: Mzoy – статический момент объема V относительно плоскости xoy (пл.Ä).
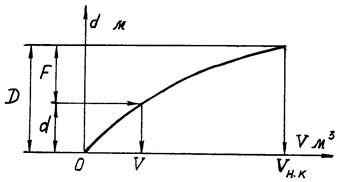 |  | ||
По результатам расчета для всех теоретических ватерлиний могут быть построены кривые V(d), хc(d), zc(d). Кривая V(d) называется кривой объемного водоизмещения или грузовым размером (рис.19). Наибольшая абсцисса кривой V(d) определяет собой полный непроницаемый объем корпуса судна.
Рис.19. Кривая объемного Рис.20. К вычислению площадей
водоизмещения криволинейных трапеций
Дата добавления: 2014-12-09; просмотров: 2377;
